Unveiling the Magic of the Modulo Operator
Just like you would use division in everyday math to find out if one number evenly fits into another, you can do the same in programming. However, there's a more elegant solution at hand: the modulo operator %.
A Visual Cue to Modulo Operation
Imagine the number 6 as a full container of water, and the number 3 as an empty cup. If you can pour the water into the empty cup such that the container becomes completely empty with no overflow or leftover, then it's safe to say 3 "neatly divides" into 6.
Why Division Falls Short
While division (/) can be used, it creates a mess. You'd need to deal with quotients and additional logic to make sense of any leftovers. This is like trying to use a measuring cylinder to manually calculate if the water can completely fill the empty cup, drop by drop.
Cumbersome, right?
The Power of Modulo (%)
Enter the modulo operator (%). This tool directly gives you any leftovers (the remainder) when you try to fit one number into another. If it gives you a zero, voila! The numbers fit perfectly.
Here's a quick example:
16 % 3
2// 0
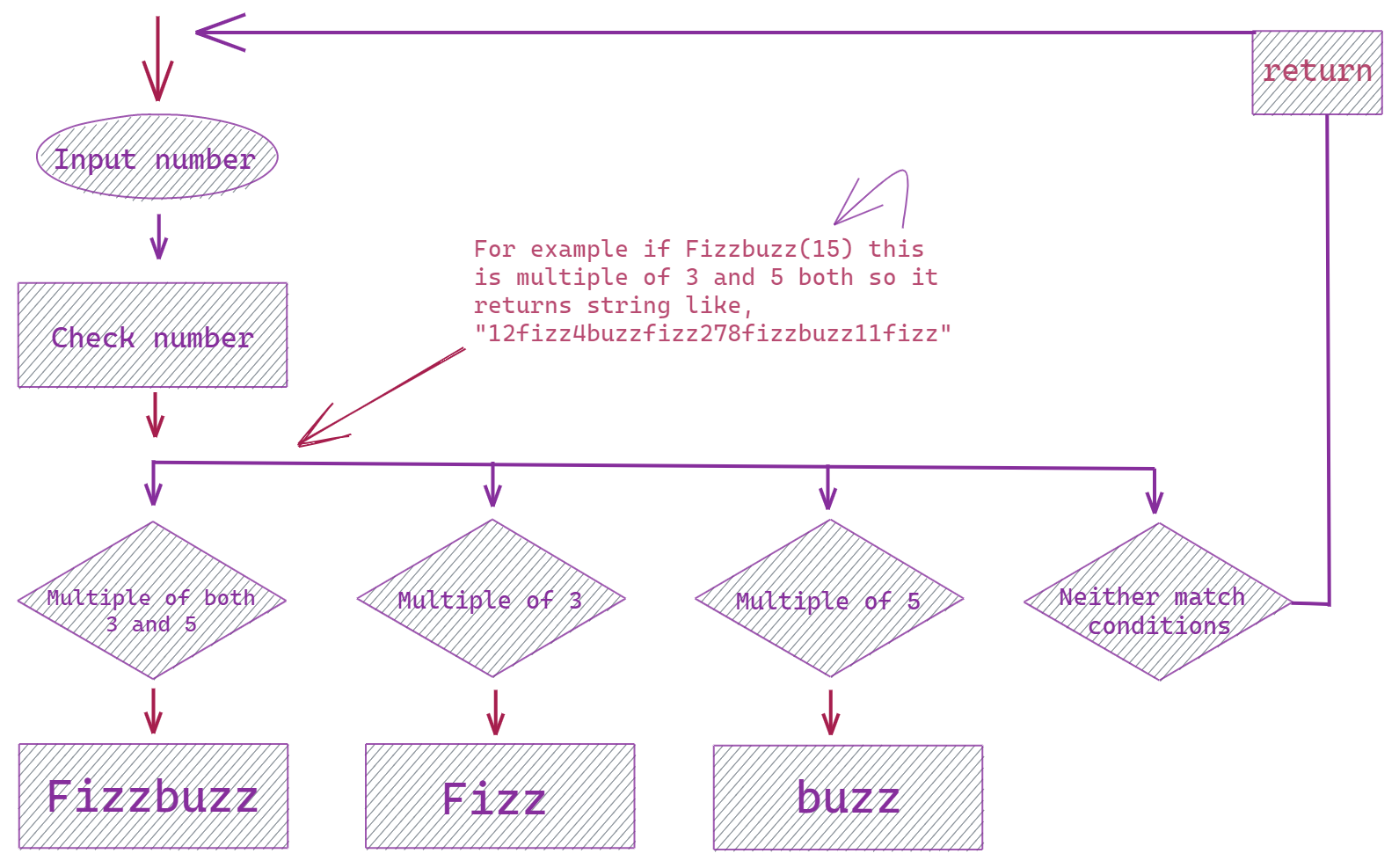
3// 3 neatly divides into 6The Practicality of Modulo in the FizzBuzz Problem
For FizzBuzz, using % is an absolute win. Just check if the number, when divided by another (say 3 or 5), leaves a remainder of zero:
- If
n % 3 == 0, it's "fizz." - If
n % 5 == 0, it's "buzz." - If
n % 15 == 0, it's "fizzbuzz."
See? No mess, no fuss. Just a neat, simple solution for identifying multiples. And this, my friends, is why the modulo operator is your best companion for problems involving division and remainders.