Let's begin by revisiting how a general hash table works, the theory being what our Hashmap data structure will be based off. As we've noted, in many programming languages, there is a Hashmap class that's based off a legacy Hashtable. Let's step through our suggested implementation of this code.

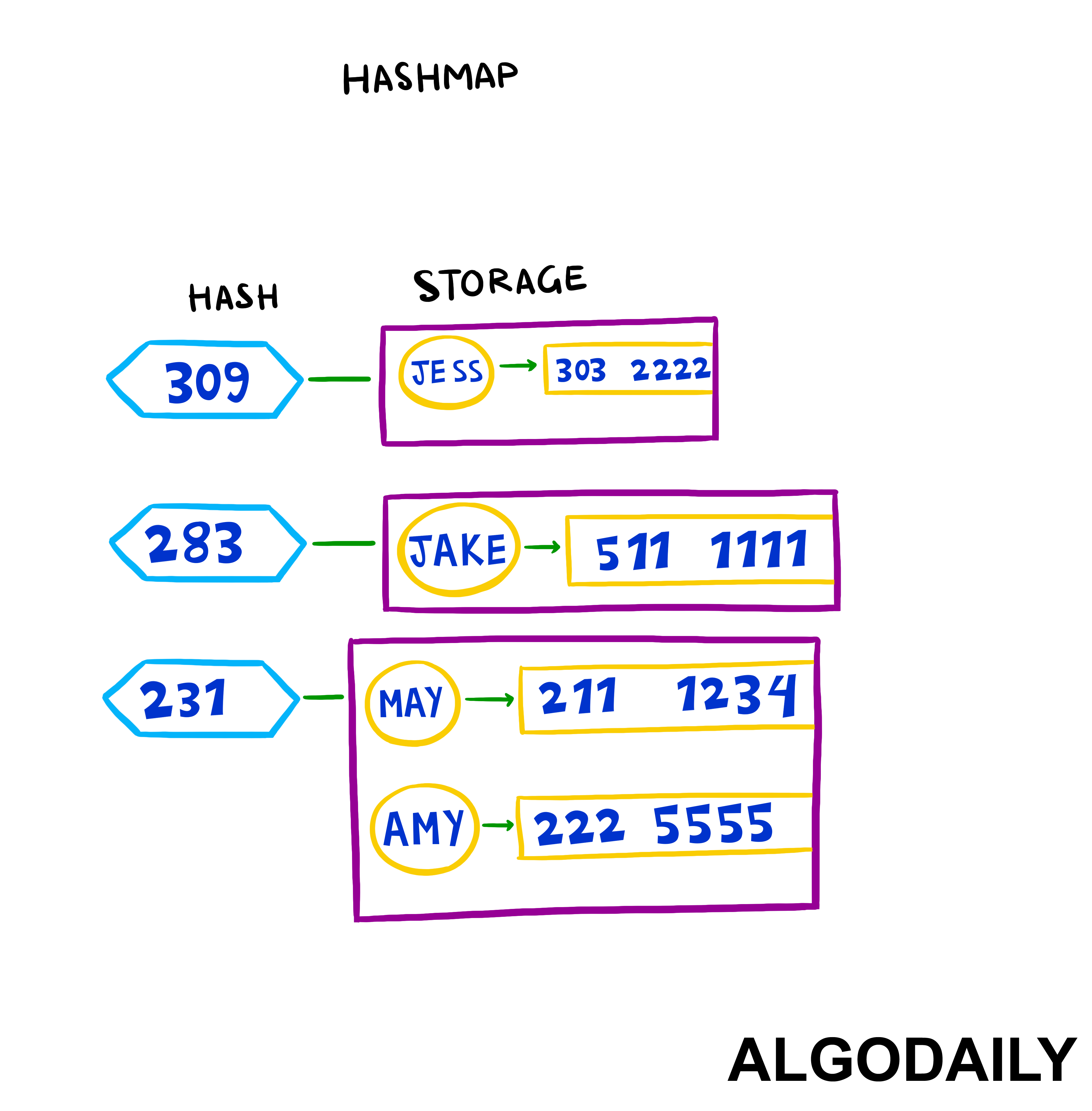
So we know that hash tables work by storing data in buckets. To access those buckets, we'll need a way to convert a key to an bucket number. (The buckets can be modeled using both arrays and binary search trees, but to keep things simple and maximize speed, we'll stick with using arrays.)

Using keys decouples us from having to know where the data is in the array. Our data structure thus needs a hash function, provided in this case as hashStr, to calculate an index into buckets where the wanted value is stored. We're essentially mapping the key to an array index via our hashStr hash function.

1hashStr('r')
2// 114
3
4// array = [  _  ,  X  ,  _  ,  _ ]
5// index     113   114   115   116