AlgoDaily - Shortest Clear Path - Shortest Clear Path

Shortest Clear Path (Hard)

Good afternoon! Here's our prompt for today.

A clear path is a path in a binary grid from the top-left cell (0, 0) to the bottom-right cell (n - 1, n - 1) such that,

All the visited cells of the path have a value of 0.
All the adjacent cells of the path are 8-directionally connected (they are different and share an edge or a corner).

Consider an n x n binary grid grid. Find the length of the shortest clear path in the matrix. If there is no clear path, return -1.

Here, n = row = column. The length of a clear path is the number of visited cells through this path.

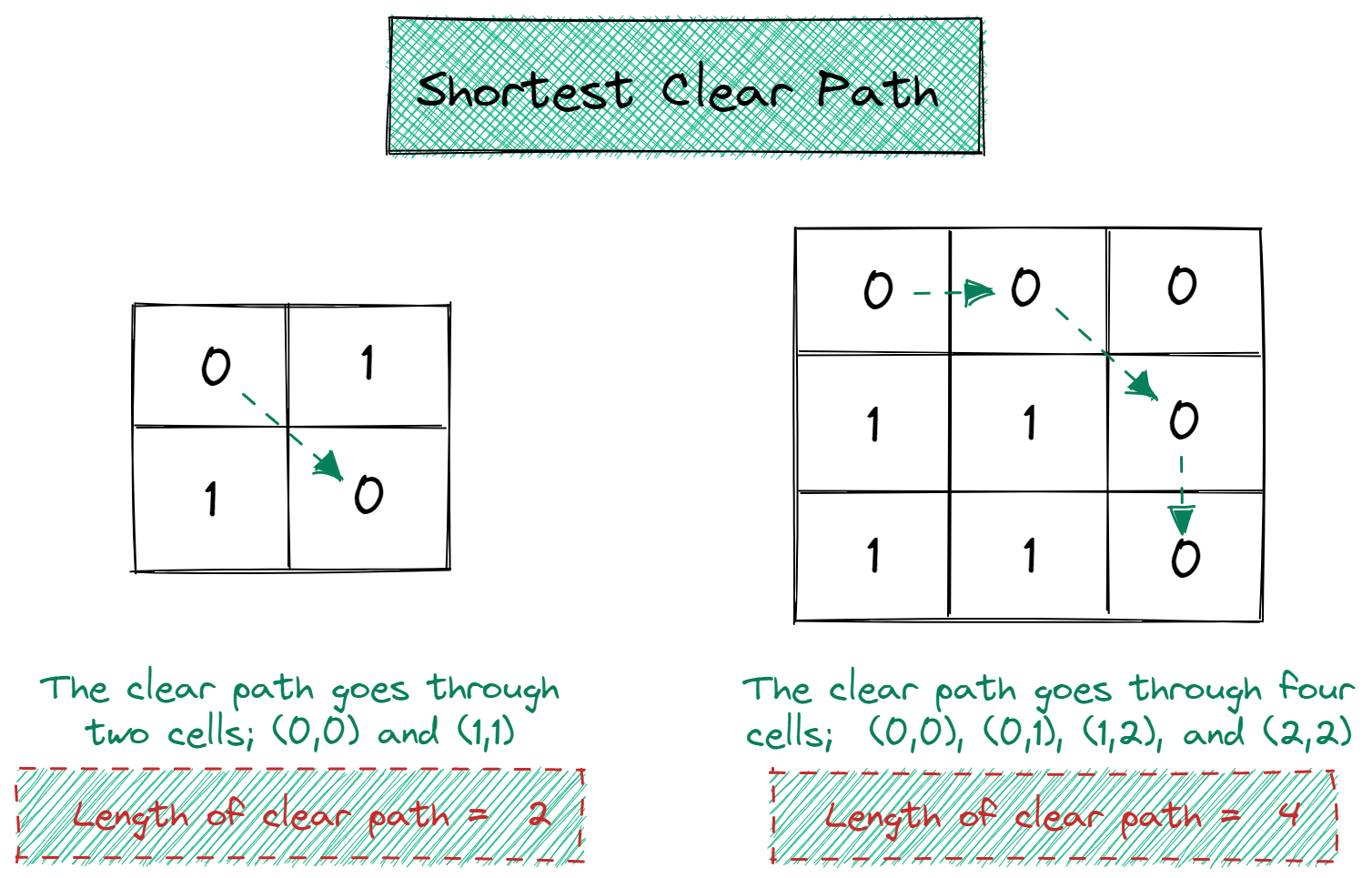
For example, consider the grids in the image above. For the 2x2 grid, only one clear path exists, and that is the shortest clear path. For the 3x3 grid, two clear paths exist. One has a length of 5 (if we include the top-right element), and the other has a length of 4 (as shown in the image). We choose the path with a shorter length, that is, the path of length 4.

Constraints

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] is 0 or 1

xxxxxxxxxx
​
 
var assert = require('assert');
​
function shortestClearPath(grid) {
    return;
}
​
​
try {
    assert.equal(shortestClearPath([
        [0, 1],
        [1, 0]
    ]), 2);
    console.log('PASSED: ' + "`shortestClearPath([[0,1],[1,0]])` should return `2`");
} catch (err) {
    console.log(err);
}
​
try {
    assert.equal(shortestClearPath([
        [0, 0, 0],
        [1, 1, 0],
        [1, 1, 0]
    ]), 4);
    console.log('PASSED: ' + "`shortestClearPath([[0,0,0],[1,1,0],[1,1,0]])` should return `4`");
} catch (err) {
    console.log(err);
}

OUTPUT

Results will appear here.