AlgoDaily - Balanced Brackets

Good morning! Here's our prompt for today.

As a software engineer, you'll often be asked to optimize programs. One of the easiest ways to do so is by the introduction of an additional data structure.

Here's another classic problem along the same vein. We're provided a string like the following: "{[])}" that is inclusive of the following symbols:

parentheses '()'
brackets '[]', and
curly braces '{}'.

Can you write a function that will check if the symbol pairings in the string follow these below conditions?

They are correctly ordered, meaning opening braces/symbols should come first.
They contain the correct pairings, so every opening brace has a closing one.
They are both of the same kind in a pair, so an opening parenthesis does not close with a closing curly brace.

For example, () is valid. (( is not. Similarly, {{[]}} is valid. [[}} is not.

Constraints

Length of the string <= 100000
The string will only consist of characters like [,],{,},(,)
Expected time complexity : O(n)
Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
var assert = require('assert');
​
function validateSymbols(str) {
  // implement this method
  return str;
}
​
try {
  assertIsFunction(validateSymbols);
​
  console.log('PASSED: ' + '`validateSymbols` is a function');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('[]'), true);
​
  console.log('PASSED: ' + "`validateSymbols('[]')` should return `true`");
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('{{[]}}'), true);
​
  console.log('PASSED: ' + "`validateSymbols('{{[]}}')` should return `true`");
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('[[}}'), false);
​
  console.log('PASSED: ' + "`validateSymbols('[[}}')` should return `false`");
} catch (err) {
  console.log(err);
}
​
function assertIsFunction(f) {
  return typeof f === 'function';
}
​

Tired of reading? Watch this video explanation!

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

The problem calls for us to maintain two parallel symbols in a string, so we'll need some way to keep track of the "balancing".

This means we'll need a certain technique which allows for keeping score of both of the following things:

We should track what's "coming in" or incoming.
We should also keep count of what's "going out" or outgoing.

Let's start to brainstorm ways of keeping that information handy and accessible.

Using a Counter?

One easy solution that may come to mind is using a counter-- a simple variable that tracks the difference in opening and closing symbols. For example, consider (()). Here's a potential algorithm:

Setup a variable counter, initialize it to 0
Iterate the input string, when we see an opening (, we increment the counter by 1
When we see a closing ) we decrement the counter by 1
If counter ever drops below 0, it's invalid because we've seen more closing brackets than the opening ones
If counter > 0 when all is said and done, some opening braces don’t have their closing counterparts
Otherwise, the string is valid

This seems straightforward and simple, but it doesn't actually work for this problem!

Why is this? Well, we're dealing with multiple type of symbols. In this case, relative order matters. Consider the following:

What else can we do?

Are you sure you're getting this? Click the correct answer from the options.

Which principle are elements in a stack data structure inserted and removed by?

Click the option that best answers the question.

Linear order
First in, first out
Minimum in, maximum out
Last in, first out

Stack to the Rescue

The easiest way to accomplish what we want is with a stack data structure, as its push() and pop() methods model the pair-wise opposing symbols in an efficient manner (the push/pop operations for most stack implementations is O(1)).

With a simple stack in place, we can start by iterating through the given string.

At each step, look for any opening/left-side symbol and push it onto the stack. Here's a sample snippet of what that looks like.

xxxxxxxxxx
 
const stack = [];
const str = "[{()}]";
​
for (let i = 0; i < str.length; i++) {
  if (str[i] === "(" || str[i] === "[" || str[i] === "{") {
    stack.push(str[i]);
  }
}
​
console.log(stack);

Then, if we encounter the opposite/pairwise symbol, we can pop() it off so that we are no longer tracking that pair.

So visualize the processing like this:

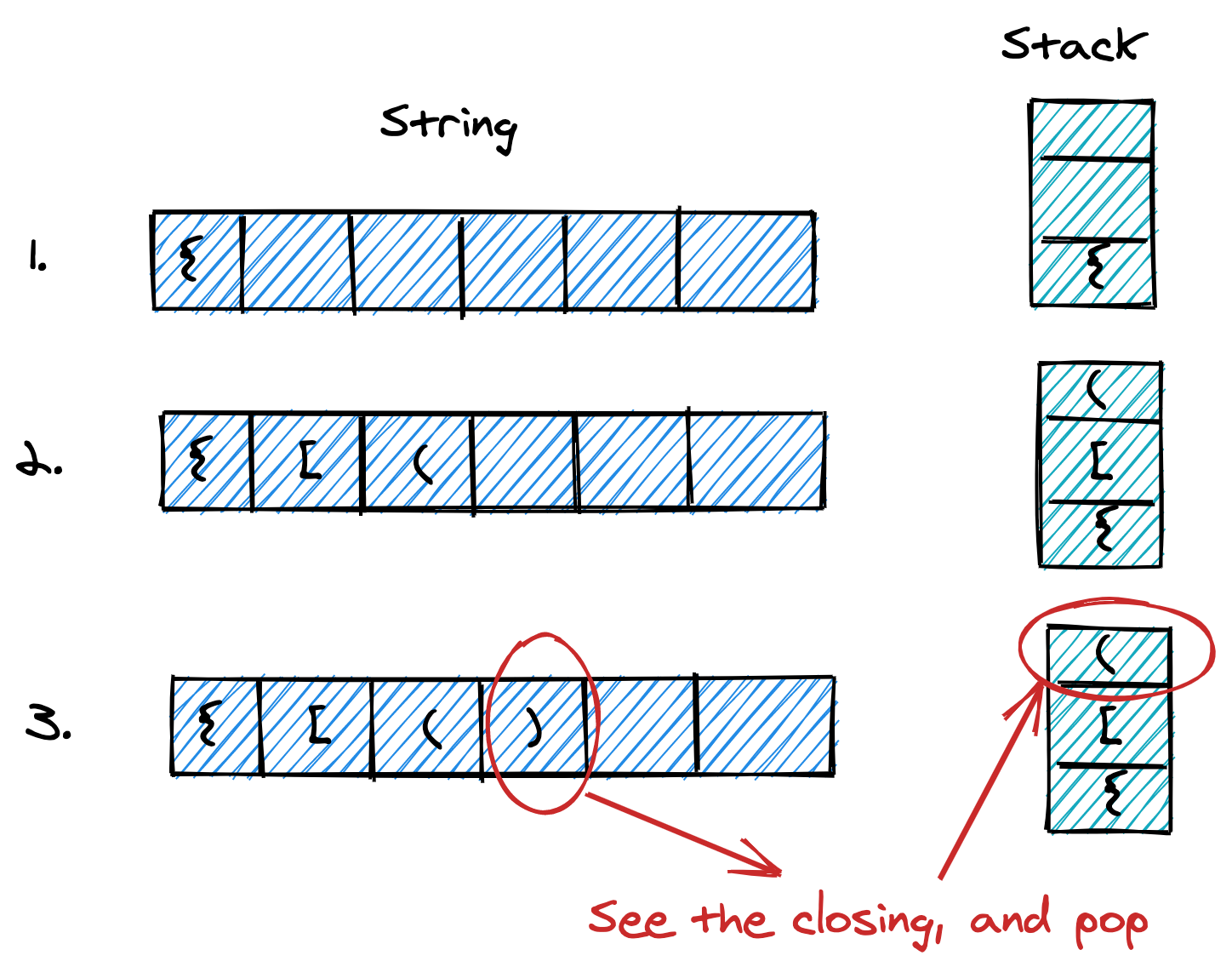
xxxxxxxxxx
 
const stack = [];
​
if (str[i] === "(" || str[i] === "[" || str[i] === "{") {
  stack.push(str[i]);
} else {
  // if the top of the stack's pairwise symbol is the next character
  if (stack[arr.stack - 1] === map[str[i]]) {
    stack.pop();
  } else return false;
}

Build your intuition. Click the correct answer from the options.

Which of the following are applications of a stack data structure?

Click the option that best answers the question.

Evaluating math expressions
Management of function calls
Evaluating prefix, postfix, and infix expressions
All of the above

Finally-- if at any time, we encounter a mismatch, we know it's an invalid string.

The time complexity is O(n), as we iterate through all the characters of the string.

One Pager Cheat Sheet

You need to write a function that will check if the symbol pairings in a string of length up to 100000 that consists of [, ], {, }, (, ) follow the conditions of being correctly ordered, paired, and of the same kind, with an expected time complexity of O(n) and an expected space complexity of O(n).
We should use a stack to keep track of incoming and outgoing symbols in order to maintain balance in a string.
Using a counter to track the difference between opening and closing symbols is not sufficient since multiple types of symbols are involved and relative order matters.
The items in a stack are inserted and removed according to the Last in, First out (LIFO) principle.
Stack data structures provide an efficient way to parse strings of opening/closing symbols with O(1) push/pop operations.
We pop() any opposite/pairwise symbols off the stack as we visualize the processing.
A Last In, First Out (LIFO) data structure, such as a stack, can be used to solve various problems, including tracking function calls, validating brackets, calculating prefix expressions, and solving mazes.
If the characters of a string do not match at any point, it is an invalid string.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
 
var assert = require('assert');
​
function validateSymbols(str) {
  let map = {
    ')': '(',
    ']': '[',
    '}': '{',
  };
  let stack = [];
  for (let i = 0; i < str.length; i++) {
    if (str[i] === '(' || str[i] === '[' || str[i] === '{') {
      stack.push(str[i]);
    } else {
      if (stack[stack.length - 1] === map[str[i]]) {
        stack.pop();
      } else return false;
    }
  }
  return stack.length === 0 ? true : false;
}
​
try {
  assertIsFunction(validateSymbols);
​
  console.log('PASSED: ' + '`validateSymbols` is a function');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('[]'), true);
​
  console.log('PASSED: ' + "`validateSymbols('[]')` should return `true`");
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('{{[]}}'), true);
​
  console.log('PASSED: ' + "`validateSymbols('{{[]}}')` should return `true`");
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(validateSymbols('[[}}'), false);
​
  console.log('PASSED: ' + "`validateSymbols('[[}}')` should return `false`");
} catch (err) {
  console.log(err);
}
​
function assertIsFunction(f) {
  return typeof f === 'function';
}

Alright, well done! Try another walk-through.

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Tired of reading? Watch this video explanation!

We'll now take you through what you need to know.

Using a Counter?

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Stack to the Rescue

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

One Pager Cheat Sheet

This is our final solution.

Alright, well done! Try another walk-through.

Programming Categories

Popular Lessons