Good morning! Here's our prompt for today.

Can you write a function to traverse a binary tree in-order, and print out the value of each node as it passes?

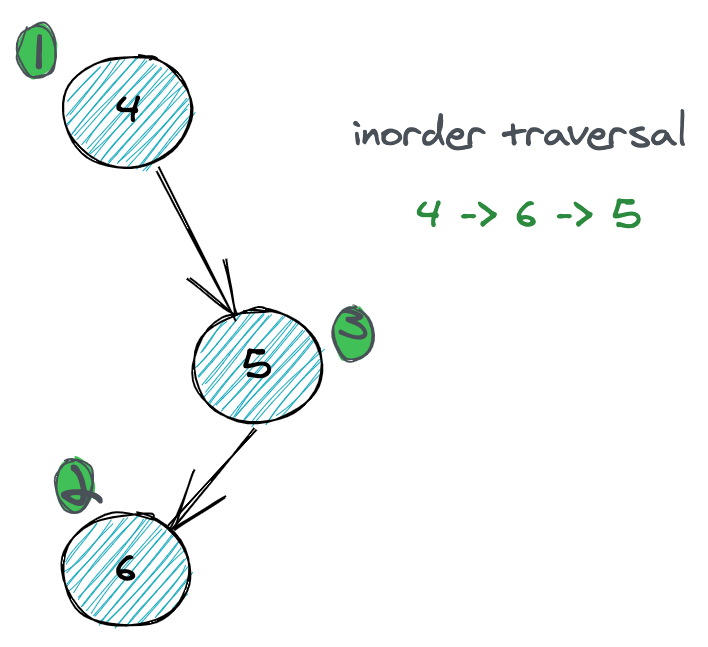
1  4
2   \
3    5
4   /
5  6

The example would output [4, 6, 5] since there is no left child for 4, and 6 is visited in-order before 5.

The definition of a tree node is as follows:

1function Node(val) {
2  this.val = val;
3  this.left = null;
4  this.right = null;
5}

Follow up: you'll likely get the recursive solution first, could you do it iteratively?

Constraints

• Number of vertices in the tree <= 100000
• The values of the vertices in the tree will be between -1000000000 and 1000000000
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  assertIsFunction(inorderTraversal, '`inorderTraversal` should be a function');

var assert = require('assert');

​

function inorderTraversal(root) {

  return root;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

​

var tree4 = new Node(5);

tree4.left = new Node(3);

Tired of reading? Watch this video explanation!

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's our guided, illustrated walk-through.

How do I use this guide?

This is one of those questions where knowing the terminology is necessary. In-order traversal visits the left child nodes first, then the root, followed by the right child (remember, it's called in-order because the current node's value is read in-between the left and right child nodes).

Recall the following ordering types:

Inorder traversal

1. First, visit all the nodes in the left subtree
2. Then the root node
3. Visit all the nodes in the right subtree

When to use? With a BST, the in order traversal will give the elements in ascending order, useful for problems where order matters.

1// pseudo-logic of the inorder function:
2inorder(root.left)
3display(root.data)
4inorder(root.right)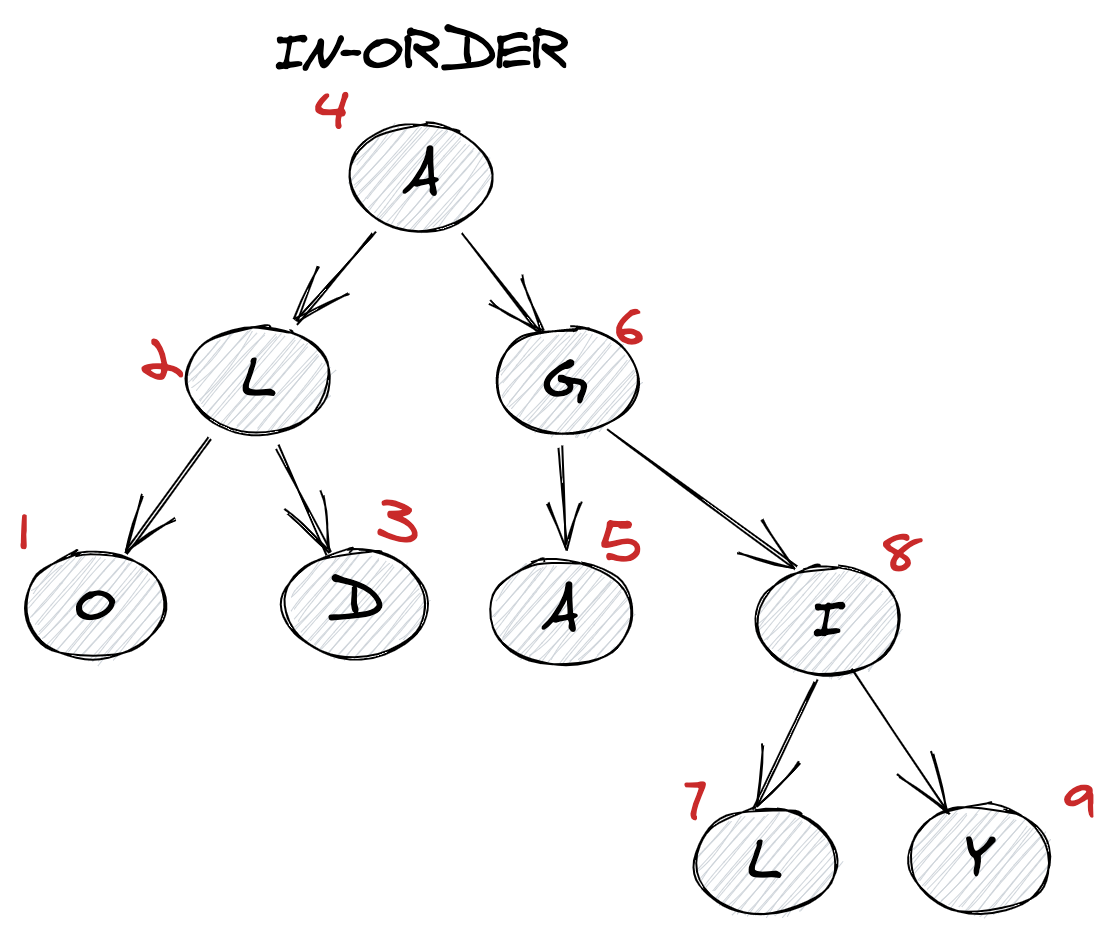

xxxxxxxxxx

function inorderTraversal(root) {

  let res = [];

  helper(root, res);

  return res;

}

​

function helper(root, res) {

  if (!root) {

    return res;

  }

  helper(root.left, res);

  res.push(root.val);

  helper(root.right, res);

  return res;

}

​

const root = {

  val: 1,

  right: {

    val: 2,

    left: {

      val: 3

    }

  }

};

​

console.log(inorderTraversal(root));

Preorder traversal

1. Visit root node
2. Then go to all the nodes in the left subtree
3. Visit all the nodes in the right subtree

When to use? You can use pre-order traversal to create a copy of the tree, since you can access each node before its subtrees. It's also used to get expressions on an expression tree.

1display(root.data)
2preorder(root.left)
3preorder(root.right)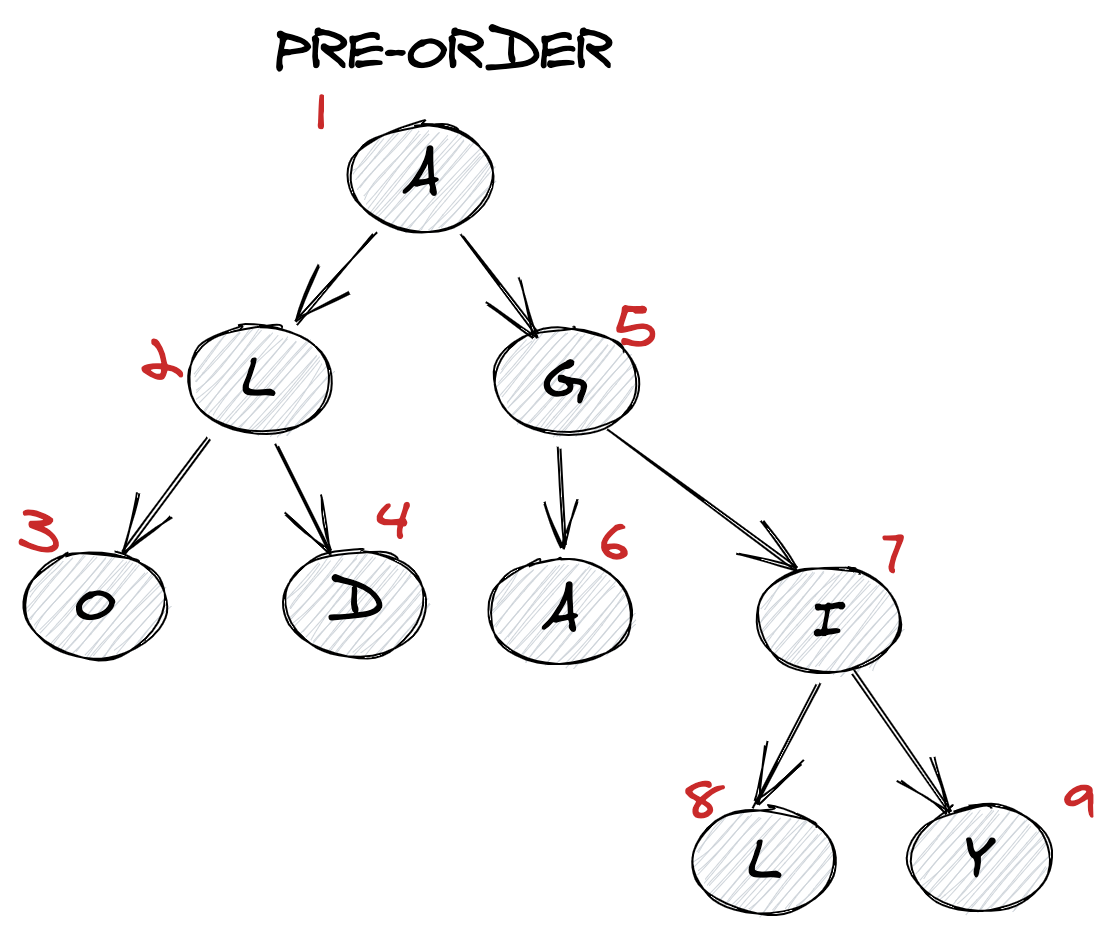

Note: This algorithm is equivalent to the famous graph algorithm Depth First Search (DFS).

xxxxxxxxxx

function preorderTraversal(root) {

  let res = [];

  helper(root, res);

  return res;

}

​

function helper(root, res) {

  if (!root) {

    return res;

  }

  res.push(root.val);

  helper(root.left, res);

  helper(root.right, res);

  return res;

}

​

const root = {

  val: 1,

  left: {

    val: 2

  },

  right: {

    val: 3

  }

};

​

console.log(preorderTraversal(root));

Postorder traversal

1. Visit all the nodes in the left subtree
2. Visit all the nodes in the right subtree
3. Visit the root node

When to use? You can use post-order traversal to delete a tree, since you can delete all of a node's children before itself.

1postorder(root.left)
2postorder(root.right)
3display(root.data)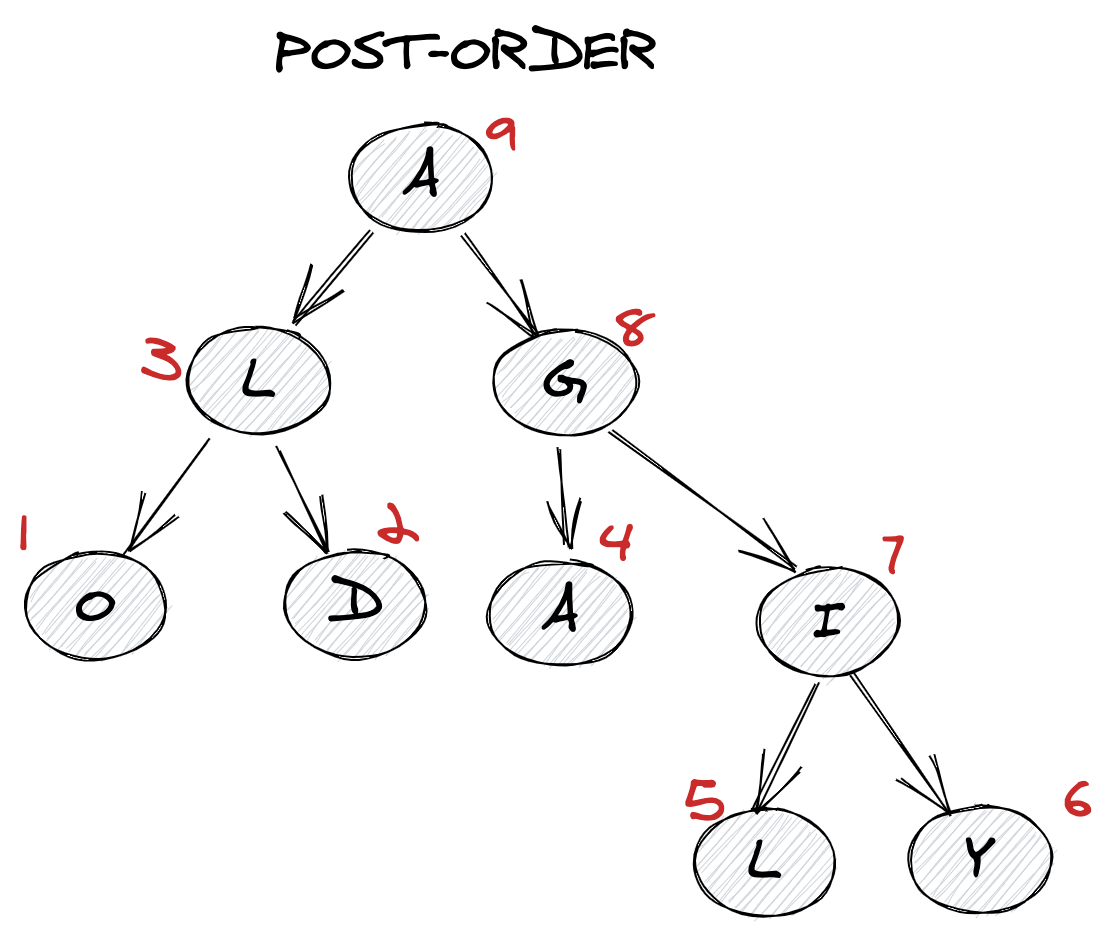

xxxxxxxxxx

function postorderTraversal(root) {

  let res = [];

  helper(root, res);

  return res;

}

​

function helper(root, res) {

  if (!root) {

    return res;

  }

  helper(root.left, res);

  helper(root.right, res);

  res.push(root.val);

  return res;

}

​

const root = {

  val: 1,

  left: {

    val: 2

  },

  right: {

    val: 3

  }

};

​

console.log(postorderTraversal(root));