AlgoDaily - An Illustrated Guide to Dijkstra's Algorithm

Home > Data Structures and Algorithms 🚀 > Draw a Graph > An Illustrated Guide to Dijkstra's Algorithm

In this lesson, we will learn about Dijkstra's algorithm, with a focus on following key points:

What is Dijkstra's Algorithm?
What are shortest path problems?
See a working implementation of Djikstra's algorithm in Python

The field of computer science encompasses a wide variety of problems. The shortest path problem is an important one, and we see many applications of it daily.

For example, we often need to find the shortest path between two points while traveling. Web mapping applications such as Google Maps use these algorithms to display the shortest routes.

The shortest path problem can be solved using different algorithms, such as Breadth-First Search (BFS), A* search algorithm, or Floyd-Warshall algorithm. However, the most popular and optimal shortest path algorithm is the Dijkstra's algorithm.

Problem Representation

Shortest path problems are represented in the form of a graph. Before moving forward, let's review our knowledge of graph concepts.

Build your intuition. Click the correct answer from the options.

A graph consists of __ and ___.

Click the option that best answers the question.

Points, edges
Nodes, edges
Vertices, lines
Any of the above

For shortest path problems, nodes represent cities (or points) and the edges represent the connectivity, or connection, from one node to another, as illustrated below. These types of problems may have one or more source nodes from which paths are determined. This problem can be both represented using either directed or undirected graphs.

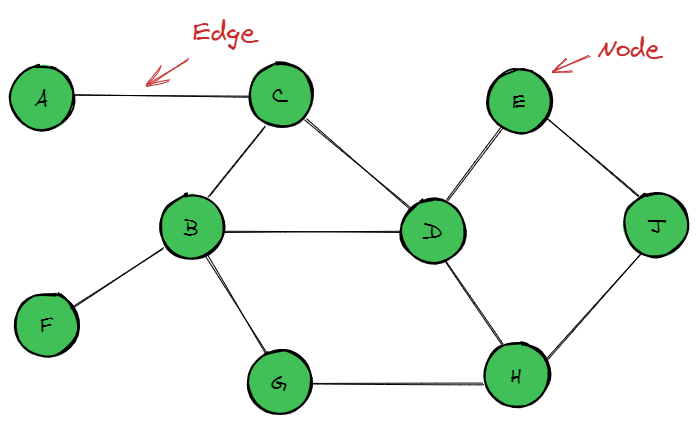
Time for another review question!

Are you sure you're getting this? Click the correct answer from the options.

Directed graphs are __ and undirected graphs are __.

Click the option that best answers the question.

bidirectional, unidirectional
unidirectional, bidirectional

Algorithm

Now that we've established the problem representation, let's discuss Dijkstra's algorithm. Dijkstra's requires the input graph to have only one source node. It also requires that all the edges in the graph have non-negative weights.

Suppose we are given a map such as the one below and wish to travel from city A to city F. In a simple graph like this, we can see that there are several paths to travel from A to F.

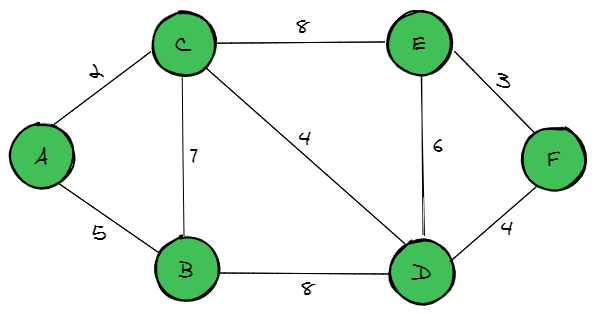
After a hard look, you'll realize that the path A -> C -> D -> F will give us the shortest path. But that required a lot of thought, and you most likely had to analyze every path one by one before coming to the conclusion.

But what if you have a more complicated graph with hundreds of cities? In such a case, you could use Dijkstra's algorithm. It makes this work easier by finding the distance values for the path for each unvisited node n. This distance value will be the shortest distance of that node n from the source node. This helps in determining the shortest path.

Let's dive deep into the algorithm by initializing some variables that are required for Dijkstra's algorithm. We'll need the following:

A list of all unvisited nodes in the graph.
A list of distances with their nodes in the graph. At first, the distance of all the nodes is initialized as infinity, except the source node (which is initialized as 0).
A list of all nodes that are visited, and which make the shortest path. At first, this list will contain the source node only.

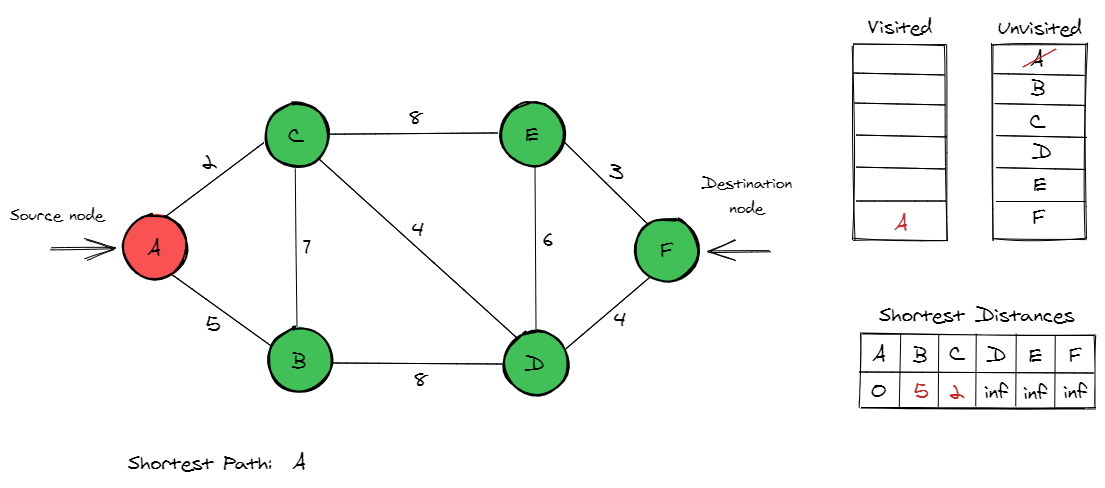
The algorithm starts from the source node, which in this case is A. We change the distances of nodes B and C in the distance list to be 5 and 2. As the sum of distance value from source node to nodes B and C is greater than the original distance, they are changed. The graph and the corresponding lists look as illustrated below.

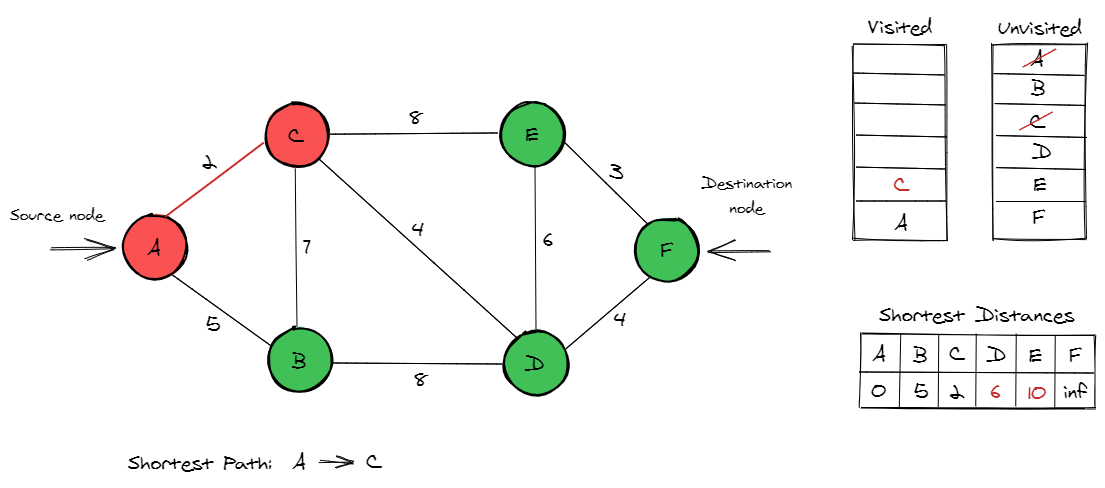
We now move towards the unvisited node with smallest distance, which is node C. The distances of nodes D and E are now updated to 6 and 10.

As the sum of the distance from the source node to nodes D and E is greater than the original distance, this was updated.

In the case of node D, the distance of A to C is 2, and C to D is 4. As such, the total distance from source node for D became 2 + 4 = 6.

Node E was updated in the same manner. Since C gives the shortest path so far, it is added to the shortest path. The changes are implemented as illustrated below.

The unvisited node with smallest distance value is now B. Since visiting B does not open any new paths, the distance values of nodes remain unchanged, and it is also not added to the path. B now moves to the visited node list.

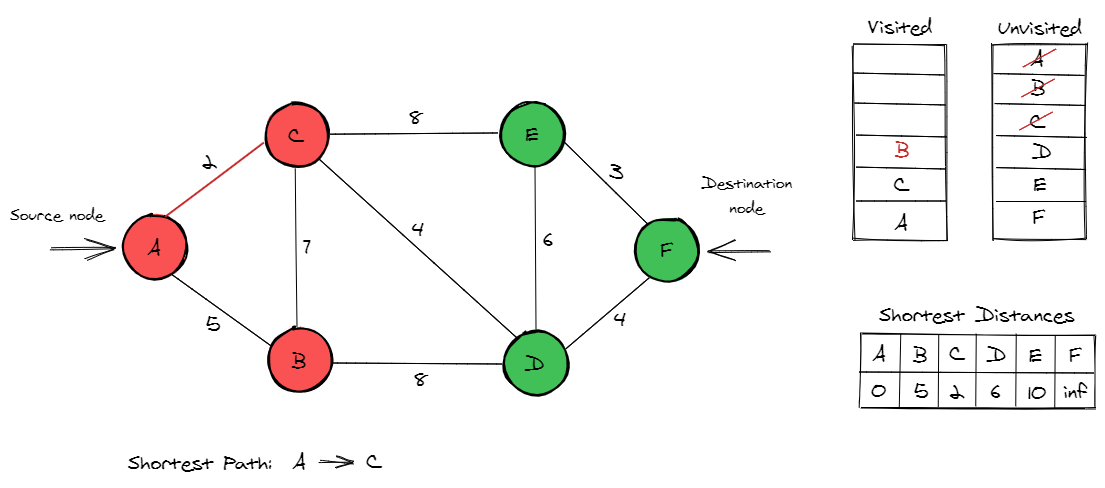
Now, D is the unvisited node with the smallest distance value. By visiting node D, we find a new connection F and update its distance value to 2 + 4 + 4 = 10. This is added to the shortest path as node D gives shortest path from the previous node C.

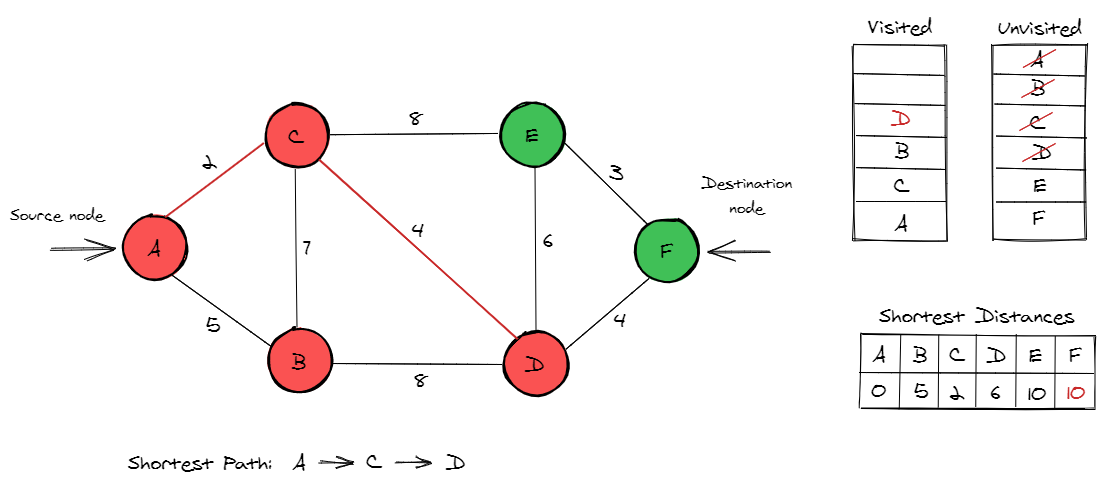
Now node E and F have similar distance values. Proceeding in lexicographic order, we will visit node E first. This does not add to the shortest path and does not change the distance values of nodes either.

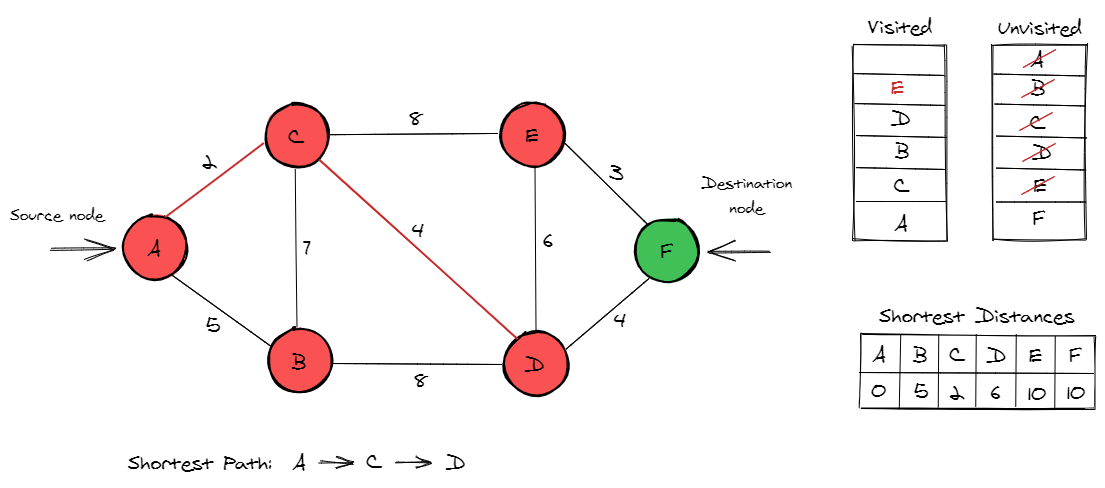
The last node to visit is F, which is also our destination node. The shortest path is now completed by adding the path from node D to F. The total weight of this shortest path is 10. All other paths that lead to the destination node F will give a larger distance than 10.

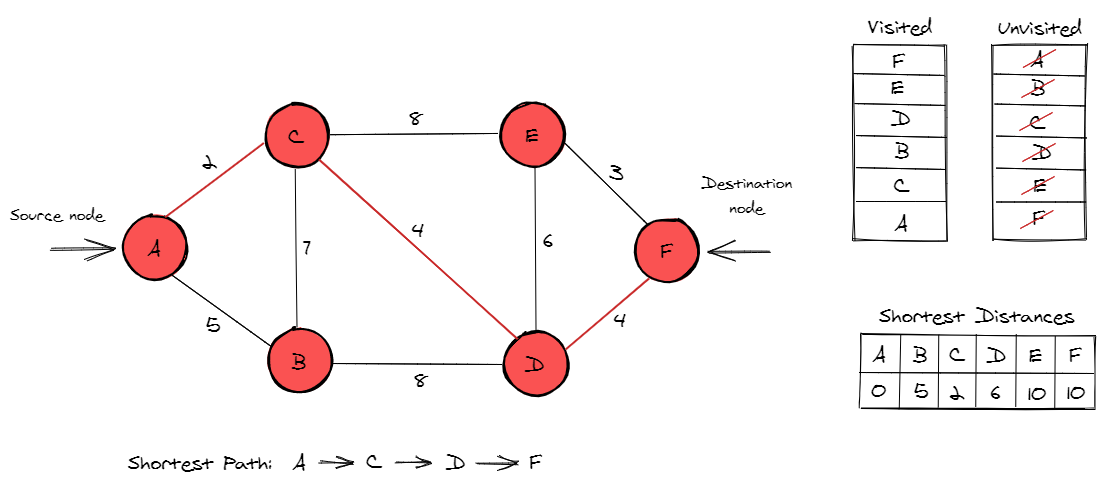
Now that we've seen an illustrative example, let's think a little more about the algorithm.

Build your intuition. Is this statement true or false?

Can Dijkstra's algorithm work on both directed and undirected graphs?

Press true if you believe the statement is correct, or false otherwise.

The direction of edges is not important in Dijkstra's algorithm. As long as the input graph is in proper format, the algorithm will give the correct output path.

Implementation

Let's implement this algorithm. You can represent the graph in different ways, but for this tutorial, we will represent it as an adjacency list (in the form of nested dictionaries).

For this implementation, we have the source node, destination node, and the example graph is represented as:

1const graph = {
2  a: { b: 5, c: 2 },
3  b: { a: 5, c: 7, d: 8 },
4  c: { a: 2, b: 7, d: 4, e: 8 },
5  d: { b: 8, c: 4, e: 6, f: 4 },
6  e: { c: 8, d: 6, f: 3 },
7  f: { e: 3, d: 4 },
8};

Now the unvisited, path, and distance lists of nodes are initialized. All the initial distance values of all nodes are set to infinity except the source node which is zero.

xxxxxxxxxx
 
const graph = {
  a: { b: 5, c: 2 },
  b: { a: 5, c: 7, d: 8 },
  c: { a: 2, b: 7, d: 4, e: 8 },
  d: { b: 8, c: 4, e: 6, f: 4 },
  e: { c: 8, d: 6, f: 3 },
  f: { e: 3, d: 4 },
};
​
const formatGraph = (g) => {
  const tmp = {};
  Object.keys(g).forEach((k) => {
    const obj = g[k];
    const arr = [];
    Object.keys(obj).forEach((v) => arr.push({ vertex: v, cost: obj[v] }));
    tmp[k] = arr;
  });
  return tmp;
};
​
const dijkstra = (graph, start, end) => {
  var map = formatGraph(graph);
​
  var visited = [];
  var unvisited = [start];
  // set distance of source to 0
  var shortestDistances = { [start]: { vertex: start, cost: 0 } };
}

This is the main part of the algorithm. An unvisited node with the shortest distance from the source node is selected. All the neighboring nodes from that node are then checked, and distances are updated. Nodes are added to the path list whenever the distance is updated. This process is repeated until all the nodes in the graph are visited.

xxxxxxxxxx
 
const graph = {
  a: { b: 5, c: 2 },
  b: { a: 5, c: 7, d: 8 },
  c: { a: 2, b: 7, d: 4, e: 8 },
  d: { b: 8, c: 4, e: 6, f: 4 },
  e: { c: 8, d: 6, f: 3 },
  f: { e: 3, d: 4 },
};
​
const formatGraph = (g) => {
  const tmp = {};
  Object.keys(g).forEach((k) => {
    const obj = g[k];
    const arr = [];
    Object.keys(obj).forEach((v) => arr.push({ vertex: v, cost: obj[v] }));
    tmp[k] = arr;
  });
  return tmp;
};
​
const dijkstra = (graph, start, end) => {
  var map = formatGraph(graph);
​
  var visited = [];
  var unvisited = [start];
  var shortestDistances = { [start]: { vertex: start, cost: 0 } };
​
  var vertex;
  while ((vertex = unvisited.shift())) {
    // Explore unvisited neighbors
    var neighbors = map[vertex].filter((n) => !visited.includes(n.vertex));
​
    // Add neighbors to the unvisited list
    unvisited.push(...neighbors.map((n) => n.vertex));
​
    var costToVertex = shortestDistances[vertex].cost;
​
    for (let { vertex: to, cost } of neighbors) {
      var currCostToNeighbor =
        shortestDistances[to] && shortestDistances[to].cost;
      var newCostToNeighbor = costToVertex + cost;
      if (
        currCostToNeighbor == undefined ||
        newCostToNeighbor < currCostToNeighbor
      ) {
        // Update the table
        shortestDistances[to] = { vertex, cost: newCostToNeighbor };
      }
    }
​
    visited.push(vertex);
  }
}

To get the shortest path, we also check if it is possible to reach the destination node from the source node, as there is a possibility that it may not be reachable. The destination node is then added to the list of routes which gives us the shortest path.

xxxxxxxxxx
 
const graph = {
  a: { b: 5, c: 2 },
  b: { a: 5, c: 7, d: 8 },
  c: { a: 2, b: 7, d: 4, e: 8 },
  d: { b: 8, c: 4, e: 6, f: 4 },
  e: { c: 8, d: 6, f: 3 },
  f: { e: 3, d: 4 },
};
​
const printTable = (table) => {
  return Object.keys(table)
    .map((vertex) => {
      var { vertex: from, cost } = table[vertex];
      return `${vertex}: ${cost} via ${from}`;
    })
    .join("\n");
};
​
const tracePath = (table, start, end) => {
  var path = [];
  var next = end;
  while (true) {
    path.unshift(next);
    if (next === start) {
      break;
    }
    next = table[next].vertex;
  }
​
  return path;
};
​
const formatGraph = (g) => {
  const tmp = {};
  Object.keys(g).forEach((k) => {
    const obj = g[k];
    const arr = [];
    Object.keys(obj).forEach((v) => arr.push({ vertex: v, cost: obj[v] }));
    tmp[k] = arr;
  });
  return tmp;
};
​
const dijkstra = (graph, start, end) => {
  var map = formatGraph(graph);
​
  var visited = [];
  var unvisited = [start];
  var shortestDistances = { [start]: { vertex: start, cost: 0 } };
​
  var vertex;
  while ((vertex = unvisited.shift())) {
    // Explore unvisited neighbors
    var neighbors = map[vertex].filter((n) => !visited.includes(n.vertex));
​
    // Add neighbors to the unvisited list
    unvisited.push(...neighbors.map((n) => n.vertex));
​
    var costToVertex = shortestDistances[vertex].cost;
​
    for (let { vertex: to, cost } of neighbors) {
      var currCostToNeighbor =
        shortestDistances[to] && shortestDistances[to].cost;
      var newCostToNeighbor = costToVertex + cost;
      if (
        currCostToNeighbor == undefined ||
        newCostToNeighbor < currCostToNeighbor
      ) {
        // Update the table
        shortestDistances[to] = { vertex, cost: newCostToNeighbor };
      }
    }
​
    visited.push(vertex);
  }
​
  console.log("Table of costs:");
  console.log(printTable(shortestDistances));
​
  const path = tracePath(shortestDistances, start, end);
​
  console.log(
    "Shortest path is: ",
    path.join(" -> "),
    " with weight ",
    shortestDistances[end].cost
  );
};
​
dijkstra(graph, "a", "f");

Build your intuition. Is this statement true or false?

Time Complexity

Before diving into this subsection, time for a quick question!

Time complexity helps us understand the time it takes for the computer to execute a certain algorithm.

Press true if you believe the statement is correct, or false otherwise.

Dijkstra's algorithm takes significant computational time. The time complexity in a general case is O(V²), where V is the number of vertices. This is improved to O(E log V) (where E is the number of edges) if the graph representation is changed to adjacency lists. While a polynomial time complexity such as O(V²) would seem high, it is better than brute force algorithms which provide much higher computational times.

You can find the full working implementation here:

xxxxxxxxxx
 
const graph = {
  a: { b: 5, c: 2 },
  b: { a: 5, c: 7, d: 8 },
  c: { a: 2, b: 7, d: 4, e: 8 },
  d: { b: 8, c: 4, e: 6, f: 4 },
  e: { c: 8, d: 6, f: 3 },
  f: { e: 3, d: 4 },
};
​
const printTable = (table) => {
  return Object.keys(table)
    .map((vertex) => {
      var { vertex: from, cost } = table[vertex];
      return `${vertex}: ${cost} via ${from}`;
    })
    .join("\n");
};
​
const tracePath = (table, start, end) => {
  var path = [];
  var next = end;
  while (true) {
    path.unshift(next);
    if (next === start) {
      break;
    }
    next = table[next].vertex;
  }
​
  return path;
};
​
const formatGraph = (g) => {
  const tmp = {};
  Object.keys(g).forEach((k) => {
    const obj = g[k];
    const arr = [];
    Object.keys(obj).forEach((v) => arr.push({ vertex: v, cost: obj[v] }));
    tmp[k] = arr;
  });
  return tmp;
};
​
const dijkstra = (graph, start, end) => {
  var map = formatGraph(graph);
​
  var visited = [];
  var unvisited = [start];
  var shortestDistances = { [start]: { vertex: start, cost: 0 } };
​
  var vertex;
  while ((vertex = unvisited.shift())) {
    // Explore unvisited neighbors
    var neighbors = map[vertex].filter((n) => !visited.includes(n.vertex));
​
    // Add neighbors to the unvisited list
    unvisited.push(...neighbors.map((n) => n.vertex));
​
    var costToVertex = shortestDistances[vertex].cost;
​
    for (let { vertex: to, cost } of neighbors) {
      var currCostToNeighbor =
        shortestDistances[to] && shortestDistances[to].cost;
      var newCostToNeighbor = costToVertex + cost;
      if (
        currCostToNeighbor == undefined ||
        newCostToNeighbor < currCostToNeighbor
      ) {
        // Update the table
        shortestDistances[to] = { vertex, cost: newCostToNeighbor };
      }
    }
​
    visited.push(vertex);
  }
​
  console.log("Table of costs:");
  console.log(printTable(shortestDistances));
​
  const path = tracePath(shortestDistances, start, end);
​
  console.log(
    "Shortest path is: ",
    path.join(" -> "),
    " with weight ",
    shortestDistances[end].cost
  );
};
​
dijkstra(graph, "a", "f");

Summary

Dijkstra's algorithm is fundamental in understanding shortest path problems. The implementation of the algorithm may seem daunting at first, but it becomes easier once you understand the basic concept. In the next part of this tutorial, we will explore more shortest path algorithms, and compare them with Dijkstra's algorithm to note the key differences between them.

One Pager Cheat Sheet

The lesson covers Dijkstra's algorithm and its application in solving shortest path problems, including its implementation in Python and comparison to other methods like Breadth-First Search (BFS), A* search algorithm, and Floyd-Warshall algorithm.
The shortest path problems are represented using a graph, requiring a solid understanding of graph concepts.
The graph in mathematics and computer science comprises two key components: vertices or nodes which represent points of connection, and edges which represent the connection between these points, and it can be directed or undirected; any missing options in the multiple choice test notwithstanding, the accurate answer must include both vertices (nodes) and edges.
In shortest path problems, nodes represent cities and edges represent connectivity, with paths determined from one or more source nodes, using either directed or undirected graphs.
In computer science, a graph is a collection of nodes and edges, with directed graphs featuring unidirectional edges, resembling one-way streets, while undirected graphs feature bidirectional edges, similar to two-way streets, with unidirectional and bidirectional describing the nature of node connectivity in these graphs.
The problem representation requires the input graph to have one source node and non-negative weights for Dijkstra's algorithm, which finds the distance values for the shortest path from the source node to each unvisited node n, aiding in determining the shortest path between complex nodes, such as hundreds of cities.
The Dijkstra's algorithm is implemented by initializing variables such as a list of unvisited nodes, a list of distances to nodes (with all initially set to infinity except the source node set to 0), and a list of visited nodes that form the shortest path; the algorithm, beginning with a source node, adjusts distances of nodes in this context.
The algorithm progresses by moving to the unvisited node with smallest distance, node C, and updating the distances of nodes D and E to 6 and 10 respectively, after finding that the sum of the source-to-node distances for these nodes is greater than the original distance.
The unvisited node with the smallest distance value, B, is moved to the visited node list, but as visiting B creates no new paths, no distance values are altered and B is not added to the path.
The unvisited node with the smallest distance value, node D, is visited to discover a new connection F, which has its distance value updated to 10 as this provides the shortest path from the previous node C.
The algorithm proceeds in lexicographic order, visiting node E first, which does not alter the shortest path or the distance values of the other nodes.
The shortest path to destination node F is completed by adding the path from node D to F, resulting in a total weight of 10, which is smaller than any other path to F.
Dijkstra's algorithm can accurately calculate the shortest path in both directed and undirected graphs, by considering the least cumulative weight from the start node and treating edges in undirected graphs as two separate directed edges.
Dijkstra's algorithm doesn't depend on the direction of edges and can represent the graph as an adjacency list using nested dictionaries.
The unvisited, path, and distance lists of nodes are initialized, setting the initial distance values of all nodes to infinity except the source node which is set to zero.
The algorithm selects the unvisited node with the shortest distance from the source, updates distances by checking all the neighboring nodes, adds nodes to the path list when distance is updated, and repeats this process until every node in the graph is visited.
To find the shortest path between nodes, the reachability of the destination node from the source node is checked, after which the destination is added to the route list if reachable.
Time complexity is an important tool that helps us estimate the efficiency of an algorithm, identify bottlenecks in the code, calculate the time taken to execute its steps, measure the speed of a process, and determine the optimal solution.
Dijkstra's algorithm has a O(E log V) time complexity using adjacency lists, which is better than brute force algorithms.
Dijkstra's algorithm is a fundamental concept for understanding shortest path problems, and will be compared to other algorithms in the next part of the tutorial.

Problem Representation

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Algorithm

Build your intuition. Is this statement true or false?

Implementation

Build your intuition. Is this statement true or false?

Time Complexity

Summary

One Pager Cheat Sheet

Programming Categories

Popular Lessons