Objective: Welcome to this exciting lesson on stacks! Here's what you can expect to gain from it:
- Conceptual Understanding: Learn what stacks are, inside and out.
- Technical Proficiency: Understand the time complexities associated with stacks, and how they compare to other data structures.
- Practical Skills: Discover how stacks can be your secret weapon in coding interviews.
Why Stacks Are Fundamental
Stacks are often one of the first chapters in a data structures course. Why? Because they are straightforward yet powerful. They serve as building blocks for more complex data structures and algorithms, making them indispensable in a programmer's toolkit.
The Blueprint: Abstract Data Types (ADTs)
Before diving into stacks, you'd usually encounter the term "Abstract Data Type" or ADT. But what is an ADT? Think of it as a blueprint for a data structure. It outlines what you can do with the data structure but leaves out the details of how these operations are implemented.
- What to Do: An ADT defines a set of operations—like push, pop, or peek in the context of a stack.
- Not How to Do: It doesn't specify whether you should implement it as an array, linked list, or some other way. That choice is up to you.
Specification Over Implementation
The emphasis here is on specification. ADTs provide a way to discuss and reason about algorithms at a high level, without getting bogged down by implementation details. This is invaluable for proving the correctness of algorithms and understanding their time complexities.
What's Next: The Stack ADT
A stack is a classic example of an ADT, and you'll soon see why. It has a simple set of operations but offers a wide array of uses, from parsing expressions to tracking execution in recursive algorithms.
The Stack: A Visual Exploration
A stack is an Abstract Data Type (ADT) that allows you to add or remove objects in a specific, last-in-first-out (LIFO) order. It's like a stack of books; you can only remove the one on top, and new books get added to the top.
A Pictorial Representation of an Empty Stack
Imagine a stack as an empty, vertical container awaiting items to be filled in. Let's visualize this using a bit of flair:

In this diagram:
- The box represents the stack. It's empty now, but it's all set to accept items.
Each horizontal line within the box is a "slot" where an item can go.
Notice how all the slots are empty? That's because we've just initialized the stack and haven't added anything to it yet.
Let's test your knowledge. Click the correct answer from the options.
Which principle are elements in a stack data structure inserted and removed by?
Click the option that best answers the question.
- Linear order
- First in, first out
- Minimum in, maximum out
- Last in, first out
Stacks: Ordered, Flexible, and Efficient
Stacks, like arrays, are ordered collections of similar data types. Interestingly, stacks can be implemented using an array as the underlying data structure, although they are flexible enough to be implemented using other structures like linked lists.
The Core Operations: Push and Pop
When it comes to stacks, two operations reign supreme:
- Push: The act of inserting an element onto the stack.
- Pop: The act of removing an element from the stack.
The Cafeteria Analogy
Imagine a stack like a stack of trays in a cafeteria. Just like you would place a tray or plate at the top of the stack, the push operation places an element at the top of the stack. When it's time to clean up, you would remove the tray from the top, similar to how the pop operation removes the last-added element from the stack.
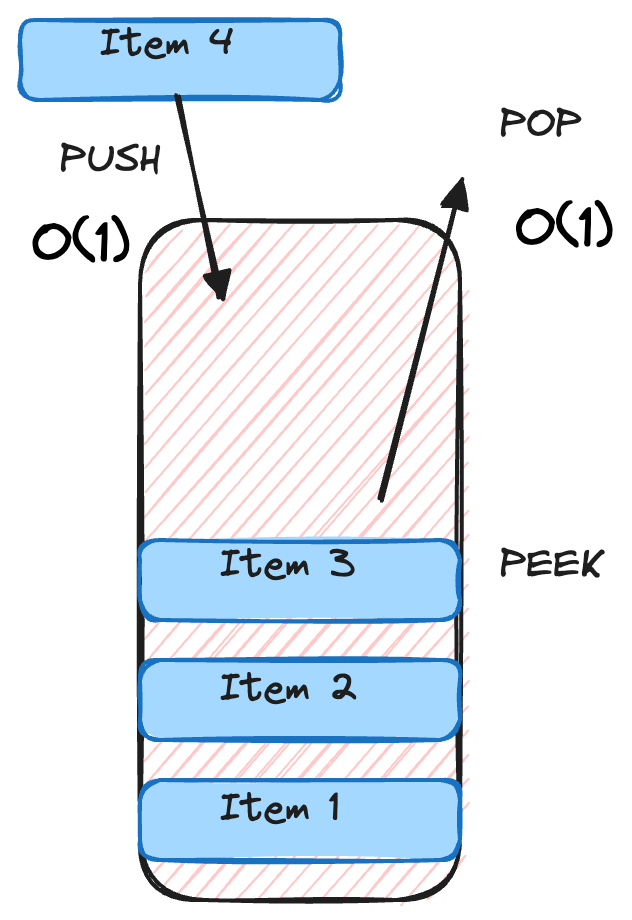
This behavior makes a stack a Last In, First Out (LIFO) data structure. The last element you put in is the first one you take out.
A Practical Example: Pushing an Element
Let's visualize pushing an element onto a stack. When we push the element 10, it becomes the bottom-most item in the stack, as shown below:

In this "box," you'll see the number 10 sitting at the bottom, signifying its place as the last-added (and currently only) element in the stack.
Adding More Elements: Stack Gets Taller
Now that we've pushed 10 into the stack, what happens when we push another element, say 20? Well, it will simply take its place on top of the last element we pushed, which is 10.
Visualizing a Stack with Multiple Elements
When we execute stack.push(20);, the stack's structure evolves as follows:
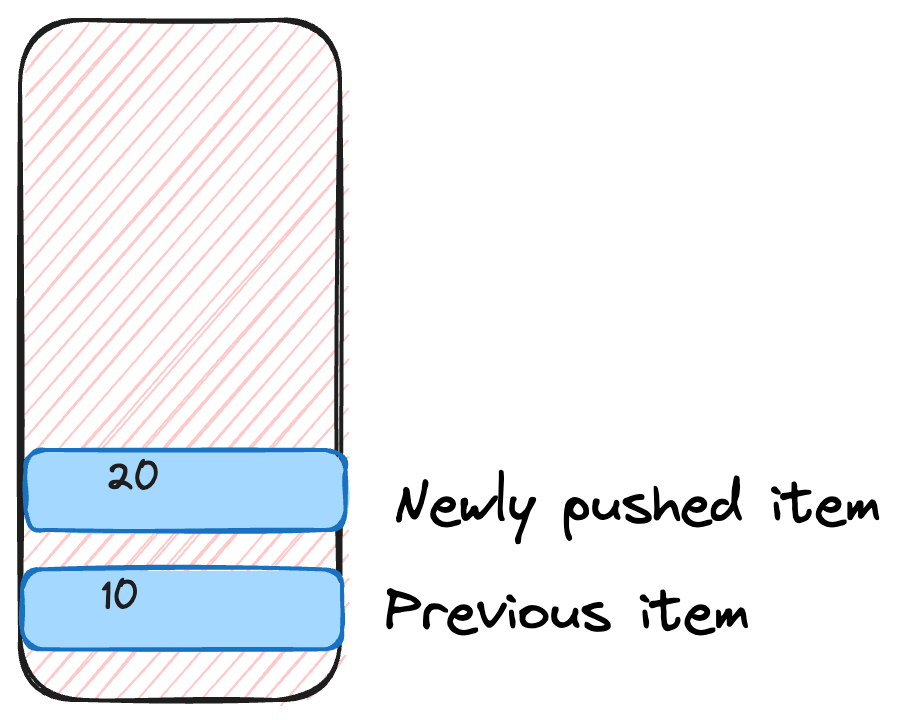 In this updated "box":
In this updated "box":10now has a companion,20, sitting right above it.20is the last-added element, making it the first one to be removed if we perform apopoperation.
Notice how 20 took its position on top of 10? This sequence of stacking elements on top of each other is a vivid illustration of the Last In, First Out (LIFO) principle in action.
Removing Elements: Stack Gets Shorter
After we've added elements to the stack, we can remove them too. This operation is called a pop. So what happens when we pop an element from our current stack?
Visualizing the Pop Operation
Executing stack.pop(); would remove the last inserted element, which is 20 in our case. Here's how the stack would look afterward:

Observations:
- The element
20has been removed from the stack. 10is now the top element again, reverting to its original role as both the first and last element in the stack.
The pop operation adheres to the Last In, First Out (LIFO) principle: it removes the most recently added element, making the previously added element the new top of the stack.
The Stack Rules: No Shortcuts Allowed
In a stack, you are restricted to adding and removing elements only from the top. This is a critical rule to remember because it means you can't skip the queue or cheat the system; you have to work your way down.
A Real-World Scenario
Let's visualize this with our example stack that has a series of numbers: 1, 434, 619, 420, 316, 1024, and 6661.
1// ____________
2// | 1 | ← Top of the stack
3// | |
4// | 434 |
5// | |
6// | 619 |
7// | |
8// | 420 | ← We want to remove this
9// | |
10// | 316 |
11// | |
12// | 1024 |
13// | |
14// | 6661 | ← Bottom of the stack
15// |____________|How to Remove a Middle Element?
Say, for instance, you want to remove 420 from this stack. You can't just reach in and pull it out. You have to remove elements from the top down. So, you'll need to execute the pop operation multiple times to get to 420.
Here's how you'd code that:
1// removing elements '1', '434', '619', '420' using a loop
2for (let i = 0; i < 4; i++) {
3 stack.pop();
4}Or, you could specify each pop operation like so:
1stack.pop(); // removes element 1
2stack.pop(); // removes element 434
3stack.pop(); // removes element 619
4stack.pop(); // finally removes element 420Either way, the point is: You have to remove the items in the reverse order they were added. And this is the core principle that makes a stack a Last-In, First-Out (LIFO) data structure.
Are you sure you're getting this? Is this statement true or false?
Stack underflow happens when we try to pop an item from an empty stack. Overflow happens when we try to push more items on a stack than its max capacity.
Press true if you believe the statement is correct, or false otherwise.
Managing Stack Capacity: When Full is Too Full
Stacks have a limit, just like many other things in life. In computational terms, this limitation is often defined when you create your stack. This is a crucial aspect of stack management you should be aware of, especially when working with stacks in languages like C++ or Java.
How Big Is Your Stack?
In many programming languages, the default size of a stack is generally large enough for most applications. However, this size can vary depending on the language or even the compiler. For instance, in C++, the default capacity is compiler-dependent and can be queried using the deque::max_size method.
1let myDeque = [];
2console.log("Maximum size of my stack: " + Number.MAX_VALUE);When Stack Overflows
A stack is considered full when it has as many elements as its capacity allows. Attempting to push an element onto a full stack results in what is known as a stack overflow. While many languages automatically manage memory and resize the stack for you, some do not. In those cases, you'll need to handle stack overflows explicitly.
When Stack Underflows
On the flip side, a stack is empty when it contains zero elements. If you try to pop an element from an empty stack, you'll encounter a stack underflow. This is another edge case you'll need to account for in your code.
1let stack = [];
2if (stack.length === 0) {
3 console.log("Stack is empty. Cannot pop.");
4}Stacks in the Real World
Stacks are a fundamental data structure with countless practical applications in computing and beyond. Here are just some examples of how stacks manifest in real-world systems and solutions:
The Back and Forward buttons in web browsers rely on a stack to keep track of your navigation history. Each page you visit gets pushed onto the stack, and clicking Back or Forward pops the stack to return you to the previous or next page.
Undo/Redo functionality in many applications like Microsoft Word leverage a stack to record state changes. Pushing edits onto a stack allows undoing them by popping the stack. Redo works similarly by pushing undone actions back onto the stack.
Stacks enable converting expressions between prefix, postfix, and infix notations. Musical notation also uses stacks to convert between time signatures.
Syntax parsing of programming languages relies on a stack to track opening and closing braces, brackets, and parentheses. Stacks ensure proper nesting and pairing.
Backtracking algorithms use stacks to explore potential solutions recursively while maintaining state to fall back on when reaching dead ends. This is useful in puzzles, games, and optimization.
Stacks track function calls and local variables at runtime. Debuggers and profilers visualize the call stack, inspiring the name of the popular programming Q&A site stackoverflow.
Reversing a string can be done by pushing characters onto a stack from left to right, then sequentially popping and concatenating them back together.
One of the most common graph algorithms, depth-first search (DFS), uses a stack to traverse nodes recursively and track paths.
As you can see, stacks offer timeless value in elegantly modeling real-world LIFO behavior and sequential processes. Their simplicity, restriction, and versatility cement their place as a foundational data structure.
Understanding Stack Complexity
Time Complexity
The stack is like a well-organized desk drawer: you always know where to find what you're looking for. Operations like push and pop are your go-to moves, and they're always fast. In technical terms, their time complexity is O(1).
- Push: Constant time
O(1)because we're adding elements to the top, and we always know where that is. - Pop: Constant time
O(1)for the same reason. We're removing from the top, and it's easy to locate.
Space Complexity
If we talk about space, well, a stack is like your bookshelf. The more books (or elements) you add, the more space it's going to take. The space complexity is proportional to the number of elements, making it O(n).
So in a nutshell:
- Time Complexity:
O(1)for bothpushandpop. - Space Complexity:
O(n).
Implementing a Stack
Here's a simple implementation of a stack. We can take it piece by piece, starting with the initial boilerplate setup:
1class Stack {
2 // Array is used to implement stack
3 constructor() {
4 this.items = [];
5 }
6
7 // Functions we'll need
8 // push(item)
9 // pop()
10 // peek()
11 // getSize()
12 // print()
13}The top is the pointer that tracks the position where new elements should be stored. If the top is equal to -1 (which is its starting point), then the stack is empty. If the top is equal to MAXSIZE, it means the stack is full. The size of this specific stack is 9.
Now check out these below methods:
1class Stack {
2 // Array is used to implement stack
3 constructor() {
4 this.items = [];
5 }
6
7 // Functions we'll need
8 push(val) {
9 // Push element into the items array
10 this.items.push(val);
11 }
12 pop() {
13 // Return top most element in the stack
14 // and remove it from the stack
15 if (!this.items.length) return "The stack has an underflow!";
16 return this.items.pop();
17 }
18 // peek()
19 // getSize()
20 // print()
21}The two important parts of a stack data structure are the pop and push functions. Before you pop, you need to check whether the stack is empty. If it’s not empty you can remove and return the last element (the element that was added to the stack last). Remember to decrement the pointer (top) before you leave the function.
Similarly, before we conduct a push operation, we need to check whether the stack is full. If not we can insert the element at the end of the stack. Remember to increment the pointer (top) before exiting the function.
Finally, you can use the main function to call push and pop functions to examine the behavior of the stack we just created. Of course, you can improve this stack by including functions like peek, getSize, etc.
xxxxxxxxxxclass Stack { // Array is used to implement stack constructor() { this.items = []; } // Functions we'll need push(val) { // Push element into the items array this.items.push(val); } pop() { // Return top most element in the stack // and remove it from the stack if (!this.items.length) return "Underflow"; return this.items.pop(); } peek() { // return the top most element from the stack // but does'nt delete it. return this.items[this.items.length - 1]; } getSize() { return this.items.length; } // print()}Linked List Implementation
We've covered implementation of a stack with an array, but did you know you can also use a linked list?
Here is another implementation of a stack using nodes of a linked list. We need to start with a Node definition.
1class Node {
2 constructor(data, next = null) {
3 this.data = data;
4 this.next = next;
5 }
6}Are you sure you're getting this? Is this statement true or false?
For the push operation of a stack implemented with a linked list, new nodes are inserted at the end. Thus, in a pop operation, nodes must be removed from the beginning.
Press true if you believe the statement is correct, or false otherwise.
Since linked lists require nodes, we will need a Node class. In each node, we have our values and our reference to the next node. If this is unfamiliar to you, I'd recommend checking out the Node Manipulation section on the site. We can use that Node definition to start setting up the class.
1class StackLL {
2 constructor() {
3 this.top = null;
4 }
5}Just like the previous example, top is the pointer which tracks the position where new elements should be stored. If the top is equal to null (which is its starting point), then the stack is empty.
1push(item) {
2 this.top = new Node(item, this.top);
3}Keep in mind that in our implementation, we're inserting data into a node. To insert within a node, we need to not only insert our item but also the reference to the next node.
In the prior snippet, we were creating a new node using the Node(int item, Node next) constructor. Inside that node, we pushed our item, creating a reference to top as the next node, and assigned top to be this new node.
1pop() {
2 if (this.top !== null) {
3 this.top = this.top.next;
4 }
5 return null;
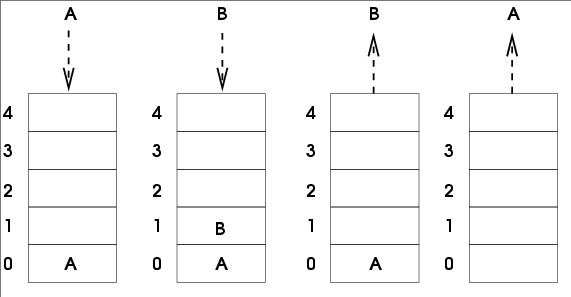
6}Here we are removing an item from the stack by moving top from the current reference node to the next reference node.
For example, top = top.next would change the reference from A to B:
1// A ----> B ----> C A ----> B ----> C
2// ^ ^
3// top top
4
5public int top(){
6 return top.data;
7}
8
9public boolean isEmpty(){
10 return top == null;
11}}There are auxiliary methods like top(), or sometimes called peek(), which are built-in functions that give you the value of what's on top of the stack. Here the top() function calls top.data which refers to the value inside of a node.
In the isEmpty() method, top is being compared to null. This is being done to check whether there is a value in the stack, or the stack is empty.
Attached is the full implementation of a stack using a linked list under the hood.
xxxxxxxxxxstack.printStack(); // Should print 2, 1class Node { constructor(value) { this.value = value; this.next = null; }}class Stack { constructor() { this.top = null; } isEmpty() { return this.top === null; } push(value) { const newNode = new Node(value); newNode.next = this.top; this.top = newNode; } pop() { if (this.isEmpty()) { return null; } const removedNode = this.top; this.top = this.top.next; return removedNode.value;Conclusion
Stacks are ADTs or Abstract Data Types because the operations of push and pop are universally unchanged. It does not matter what data structure you use to implement it or what language you write it in, the specification does not change.
Try solving the following problems to see whether you grasped the concept of Stacks:
One Pager Cheat Sheet
In this lesson, we'll cover the concept ofAbstract Data Types (ADTs), and focus on learning aboutstacksand its time complexities, as well as how to use them in programming interviews.- A Stack is an
ADTthat allows for the addition and removal of objects in a specific order. - A stack is a data structure that follows the
Last in, First out(LIFO) principle by requiring all items to beaddedorremovedfrom thetopso that the most recent element is always the first one to beremoved. - A
Stackis aLast In, First Out (LIFO)data structure, where elements are only inserted or removed from the top, similar to "stacking" trays or plates in a cafeteria. 10gotpushedto the bottom and20has now beenpushedonto the stack, making20the first and last element.- When the
stack.pop()method is used, the last inserted element (in this case20) is removed, resulting in10becoming the sole first element. - In a
stack, you can onlypopelements off the top, meaning that in order to remove an element from somewhere in the middle, you must pop off all the elements above it first. - Stack overflow occurs when we try to push an element onto a stack already at
max capacity, and stack underflow happens when we try to pop an element from an empty stack. - You need to define a size for the
Stackclass so that it is not in anoverfloworunderflowstate, although the default inC++is usually sufficiently large. Stacksare commonly used for browser navigation, Windows operations, expression notation, syntax parsing, backtracking, memory monitoring, string reversing and a popular graph algorithm,DFS.- The
pushandpopoperations are of constant time complexityO(1), while the space complexity isO(n). - We can implement a
Stackby initializing an array of sizeMAXSIZEforstack[]and using methods such aspush(),pop(),peek(),getSize()andprint(). - The
topof a stack with aMAXSIZEof9is used to determine if the stack is empty or full and also indicates the position of where new elements must be stored. - A stack
data structureconsists of important functions such as pop and push, followed by operations such aspush,pop,peek,getSize, etc. that are all called within themainfunction. - We can implement a stack using
Nodesof aLinked Listin multiple programming languages. - We can
create aNodeclassand then use it to start setting up ourStackLLclass with thetopnode initialized asnull. - When
topis notnull,pushadds a new element to the stack by makingtoppoint to a newNodecontaining the item. - We inserted our item into a
Node, creating a reference totopas thenext Nodeand assigningtopto this new node. - We remove an item from the stack by changing the
referencenodefrom the current top node to the next one, i.e.top = top.next. - The
top()function is used to check thetop.datavalue in a node; the isEmpty() method then comparestopto null to check if the stack has a value or is empty. - Stacks are
Abstract Data Typeswhich remain unchanged regardless of the underlyingdata structureand programming language used to implement them.

