This is an O(n^2) solution because it would require passing through each number, and then at each number scanning for a count.
A better way to do this is to take advantage of the property of a majority element that it consists of more than half of the set's elements.
What do I mean by this? Let's take another example, [4, 2, 2, 3, 2].
2 is obviously the majority element in the example from a visual scan, but how can we tip the algorithm off to this? Well, suppose we sorted the array:

[2, 2, 2, 3, 4]
Notice that if we hone in on index 2, that we see another 2. This is expected-- if we sort an array of numbers, the majority element will represent at least 50% of the elements, so it will always end up at the Math.floor(nums.length / 2)th index.
Depending on the sorting algorithm, this technique is usually O(n * log n) and requires either O(1) space if the sort is in-place, or O(n) space if not.
Another Method
Yet another way to solve this is to use the speed of a hash map! Hash maps allow access/look-ups in constant time, and its keys are guaranteed to be unique.
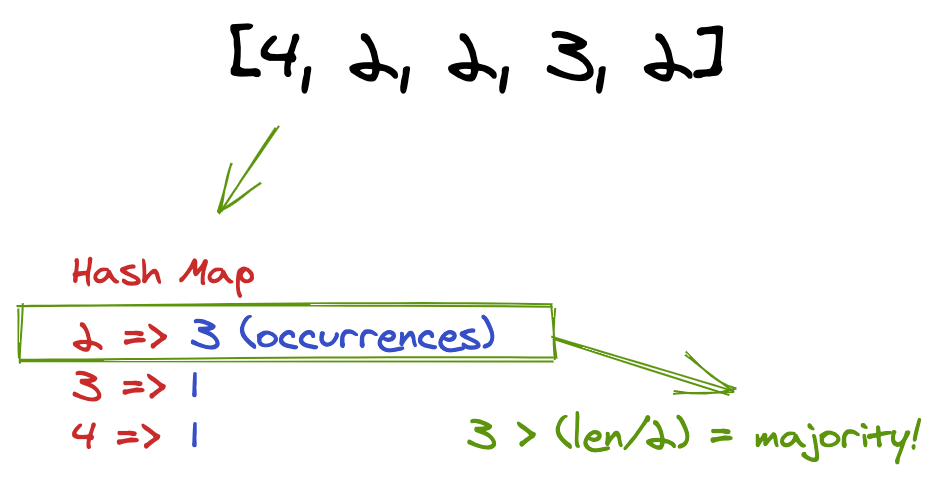
Thus, we can iterate through [2, 2, 2, 3, 4], and store each unique value as a key, and its attached value being the count. Each time we pass it, we increment its count, and use that information to relay we've got a current majority candidate.
1def majority_element(nums):
2 hash = {}
3 # we keep a local max variable to track what
4 # element is in the majority
5 max, val = 0, None
6
7 for i in range(0, len(nums)):
8 # increment or initialize the num as a key
9 if nums[i] in hash:
10 hash[nums[i]] += 1
11 else:
12 hash[nums[i]] = 1
13
14 if hash[nums[i]] > max:
15 max = hash[nums[i]]
16 val = nums[i]
17
18 return val
19
20print(majority_element([4, 2, 2, 3, 2]))The time complexity of this solution is O(n) as it requires just one pass through the array, but has a space complexity of O(n) since it needs to maintain an auxiliary hash table.