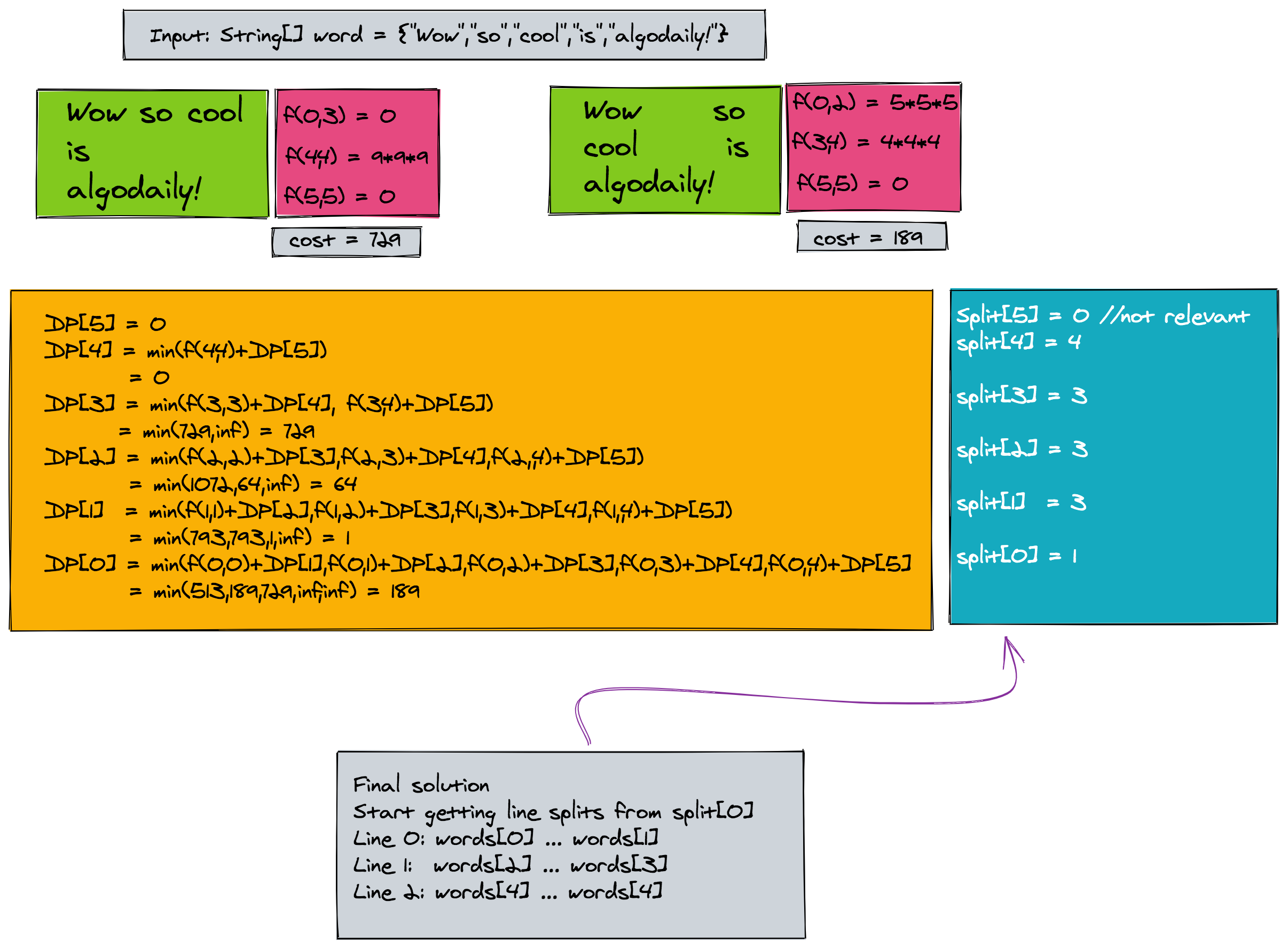
Formulation of Dynamic Programming

The problem of text justification can be solved using dynamic programming as it can be divided into sub-problems, each having a recursive sub-structure. We'll define an overall cost function DP[i], associated with each word as given by:

1DP[i] = minimum cost of justifying text that starts with word[i]

DP[i] can be defined in terms of the function $f(i,j)$, that we defined above:

1DP[n] = 0
2DP[i] = min(f(i,j)+DP[j+1]) where min is over j=(i+1)...(n-1)
3        and i=0..(n-1)

This gives us a convenient and easy method of finding the word boundaries for each line. Hence we can define split[i], which stores the index of the word that ends the line starting with word[i], in an optimal arrangement.

1split[i] = argmin(f(i,j)+DP[j+1]) where argmin is over j=(i+1)...(n-1)
2            and i=0..(n-1)

The final solution's overall cost is DP[0]. Figure below shows DP array for all words of our input word array, with an optimal minimum cost of 189.