Objective Function

For any optimization problem, we have to define the objective function or the fitness function. This is defined as a function that "attempts to maximize profits or minimize losses based on a set of constraints and the relationship between one or more decision variables".

In the case of text justification, the optimization function is dependent upon the number of white spaces being added to each line.

The more the spaces, the poorer "the performance". Hence, we want to minimize the total number of extra spaces that occur in a line.

Based on this idea, the objective function is defined as such: we have a higher value if there are more spaces between words. The goal is to find an arrangement of text that minimizes the objective function.

Let's consider what pieces of information we need. We'll use the following notations in this tutorial. Feel free to refer back to this if you ever get lost.

1n       = total number of input words
2L       = total number of lines in our solution
3word[i] = word at index i
4f(i,j)  = cost function for a line that starts at word[i] and ends at word[j]
5cost    = overall cost of the solution

Based on the above notations, let's define width(i, j)-- our objective function-- as:

By using width(i, j) to measure spacing, we have defined the cost function $f(i,j)$ associated with a line that starts with word word[i] and ends at word word[j]. Note that this function is zero for the last line, as we need not add any extra space there.

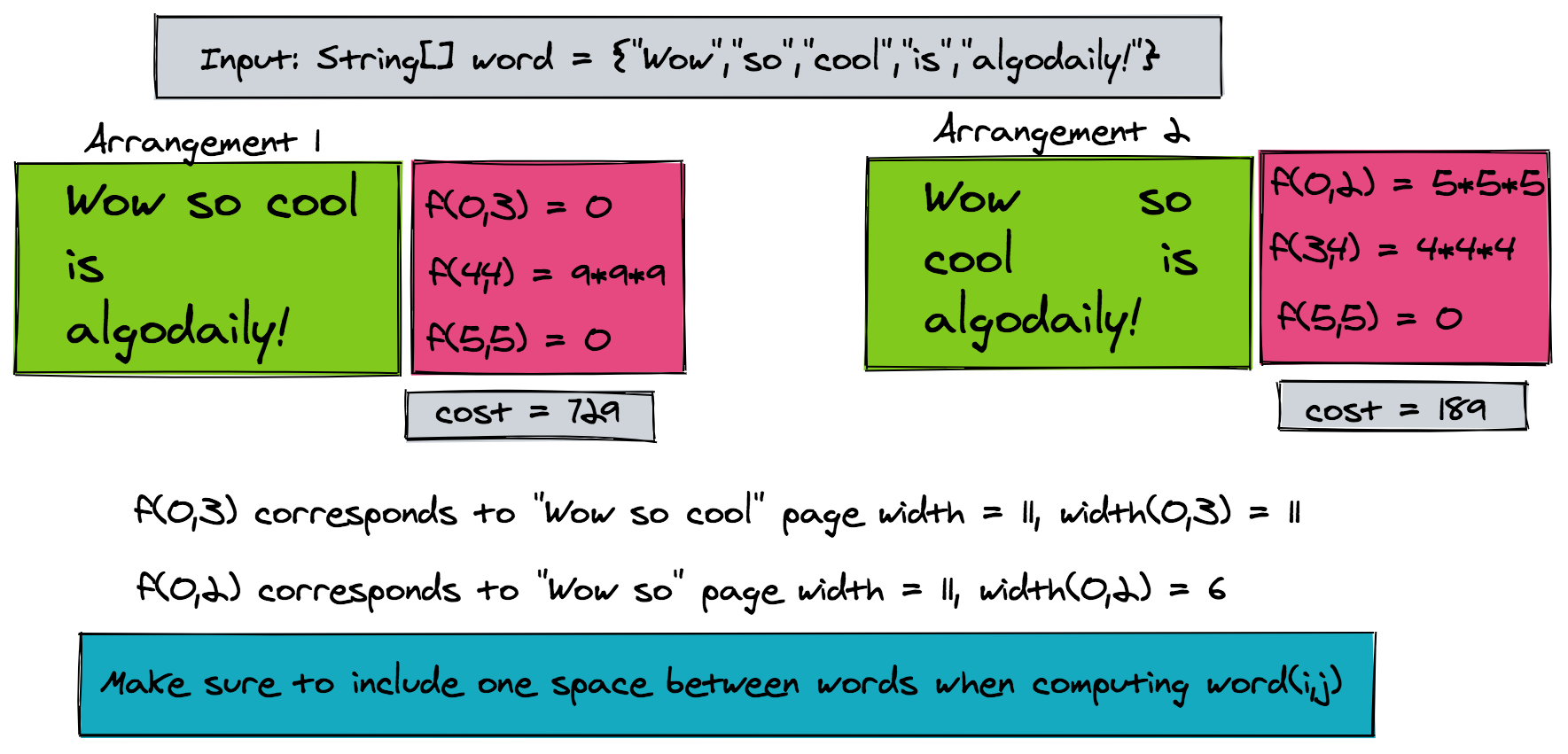
The figure below shows the example of computing $f(i,j)$ and its corresponding cost for two different arrangements. Our aim is to choose those lines for which the above cost function is a minimum. Hence, we have to find, the indices of the words that lie at the line boundaries, i.e.,:

$\text{find:}{k}_1,k_2,\dots ,k_{L-1}$

Armed with the above concepts, we are now ready to define our dynamic programming problem.