Good morning! Here's our prompt for today.
What is the best way to find out if a linked list contains a loop? You're given the following data structure as the definition of a linked list node:
1class LinkedListNode {
2 constructor(val) {
3 this.val = val;
4 this.next = null;
5 }
6}A loop or a cycle in graph theory is a path of nodes and edges where a node is reachable from itself.
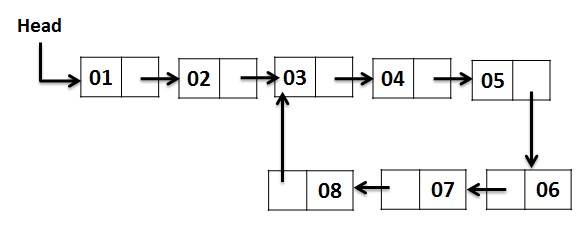
Implement a detectLoop method that takes a linked list head node as the parameter and returns true or false depending on whether there's a cycle.
Constraints
- Length of the linked list <=
10000 - Value stored in each node will be between
-1000000000and1000000000 - Expected time complexity :
O(n) - Expected space complexity :
O(1)
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxdef detectLoop(head): # fill this in return False# Node definitionclass Node: def __init__(self, val): self.val = val self.next = Nonedef create_nodes(head, nodes): for val in nodes: new_node = Node(val) head.next = new_node head = new_nodelist1 = Node(3)nodes1 = [4, 5, 6, 7, 8, 9, 10]create_nodes(list1, nodes1)list2 = Node(1)nodes2 = [2, 3, 4, 5, 6, 7, 8]create_nodes(list2, nodes2)def list_to_str(head):Here's our guided, illustrated walk-through.
How do I use this guide?
Build your intuition. Is this statement true or false?
A walk is a sequence of at least two vertices where nodes and edges may repeat. A cycle is a sequence of at least two vertices where nodes and edges cannot repeat.
Press true if you believe the statement is correct, or false otherwise.
Image credit to https://www.includehelp.com
Usually linked lists end with a node with no next reference, but we're looking for a sequence with a next pointer to a previous node. What might be the brute force solution here?
xxxxxxxxxx// 1 -> 3 <-> 5// |// 7In the above example, once we get to the second 3 node, how do we know we've got a cycle? We need some reference that we've previously encountered this vertex before.
What if we used a nested loop for tracking purposes? Let's take a look at what would happen in pseudocode:
xxxxxxxxxxiterate through 1 -> 3 -> 5 -> 3 -> 7 iterate through what we've seen so farAt outer loop node 1, we'd inner loop through 1.
At outer loop node 3, we'd inner loop through 1 -> 3.
At outer loop node 5, we'd inner loop through 1 -> 3 -> 5.
At outer loop node 3 again, we'd inner loop through 1 -> 3 -> 5 -> 3.
So the brute force way to do it is to conduct a nested traversal-- we can traverse all the nodes, and then at each iteration, traverse through the nodes already visited by the outer loop. In the inner loop, if we encounter a node twice, we know it's been repeated.
Build your intuition. Click the correct answer from the options.
The minimum number of pointers needed in the optimized algorithm is:
Click the option that best answers the question.
- 1
- 2
- 3
- 4
Let's test your knowledge. Is this statement true or false?
A linked list is a linear data structure.
Press true if you believe the statement is correct, or false otherwise.
Are you sure you're getting this? Click the correct answer from the options.
Which of the following is an advantage of Arrays over Linked Lists?
Click the option that best answers the question.
- Arrays can contain different types of data elements
- Accessing an element in an array is faster
- Insertions in Arrays is faster
- Deletions in an Array is faster
Are you sure you're getting this? Fill in the missing part by typing it in.
In a doubly linked list, traversal can be preformed in ___ directions.
Write the missing line below.
The fastest method is to traverse the linked list using two pointers. This is a well known Computer Science technique: move one pointer by one node at a time, and the other pointer by two at a time.
If these pointers meet at the same node, then there's a loop. If the pointers don't meet, then the linked list doesn’t have a loop.
The intuition here is that the faster pointer will go through the entire list at least once, and will inevitably meet the slower node at the beginning again. If there is a loop, they'll eventually converge.
Build your intuition. Fill in the missing part by typing it in.
The pointer algorithm that moves through a sequence at two different speeds is called ___.
Write the missing line below.
Another way to think about it, notice that the distance between the two pointers increase by 1 after every iteration (one travels by 2, one travels by 1, so the distance increases). The distance is always going to be original distance + distance increase each iteration (which is 1, 2, 3, ..). Because they are moving in a fixed-length cycle, they'll eventually meet.
The space complexity of the algorithm is O(1).
Build your intuition. Fill in the missing part by typing it in.
The time complexity of the above algorithm is __.
Write the missing line below.
Build your intuition. Click the correct answer from the options.
Which of the following is not a type of linked list?
Click the option that best answers the question.
- doubly linked list
- singly linked list
- circular linked list
- hybrid linked list
Try this exercise. Is this statement true or false?
In circular linked list, last node of the list points to the first node of the list.
Press true if you believe the statement is correct, or false otherwise.
Are you sure you're getting this? Fill in the missing part by typing it in.
A __ does not contain null pointer in any of its nodes
Write the missing line below.
Build your intuition. Fill in the missing part by typing it in.
Asymptotic time complexity to add an element in a linked list is ___.
Write the missing line below.
One Pager Cheat Sheet
- To detect a loop in a
linked list, implement adetectLoopmethod to take thelinked listhead node as the parameter and returntrueorfalseaccordingly with the constraints oftimeandspacecomplexities ofO(n)andO(1), respectively. - A
walkis a path through a graph that can either besimpleormultiple, and acycleis a closed walk with no vertex/edge repetitions, starting and ending at the same vertex. - A
brute forcesolution to detect aloopin a linked list might be to manually traverse each node and check if there is any node that has anextpointer to a previous node. - We can use a
nested loopto check for cycles in a graph by keeping track of the previously-encountered vertices. - We can solve this problem by
nested traversal, which requires us to traverse each node and then re-traverse the nodes already visited in the outer loop to identify any nodes that have been repeated. - The optimized algorithm only needs two
pointersto traverse the graph, withconstant space complexity, to detect any duplicate nodes. - A
Linked Listis a linear data structure composed of multiple nodes, each containing data and a pointer to the next node, allowing for efficient insertion, deletion, and navigation. - The key advantage of an array over a linked list is that it is much faster to access an element due to its contiguous block of memory, allowing random access with a calculatable memory address, contrasted with the nodes and pointers of linked lists, which requires node traversal.
- A
doubly linked listprovides efficient traversal bothforwardandbackwardcompared to asingly linked list, which only offersforwardtraversal. - By using two pointers to traverse the linked list - one slow and one fast - we can detect whether there is a loop present.
- Floyd's Cycle-Finding Algorithm is a well-known Computer Science technique used to detect if there is a loop in a
linked listby moving two pointers at different speeds through the list. - Two pointers will
meetin afixed-length cycledue to theirdistance increase of 1 per iteration, resulting in anO(1)space complexity. - The algorithm has a time complexity of O(n), as it
traversesthe arrayntimes to reach its end. - Hybrid linked list is a combination of different types of linked lists to create a unique list, rather than an existing type of linked list.
- A
circular linked listhas a pointer from the last node to the first node, forming a loop rather than a NULL pointer. - A
circular linked listprovides an infinite loop-like structure in which each node contains the address of the next node, eliminating the need for anullpointer. - The time complexity to add an element to a
linked listisO(n)due to the need to traverse the entire list to find thenull pointer.
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx print("Nice job, 1/1 tests passed!")# function to detect loopdef detectLoop(head): slow_p = head fast_p = head while slow_p and fast_p and fast_p.next: slow_p = slow_p.next fast_p = fast_p.next.next if slow_p == fast_p: return True # if they never match return False# Node definitionclass Node: def __init__(self, val): self.val = val self.next = Nonedef create_nodes(head, nodes): for val in nodes: new_node = Node(val) head.next = new_node head = new_nodelist1 = Node(3)nodes1 = [4, 5, 6, 7, 8, 9, 10]create_nodes(list1, nodes1)list2 = Node(1)Alright, well done! Try another walk-through.
If you had any problems with this tutorial, check out the main forum thread here.
