- Essentials
- Specialties
- Nontechnical
- Personalized
- Generate a Custom Course 🪄
- Guided
- 60 Day Interview Crash Course

Graphs
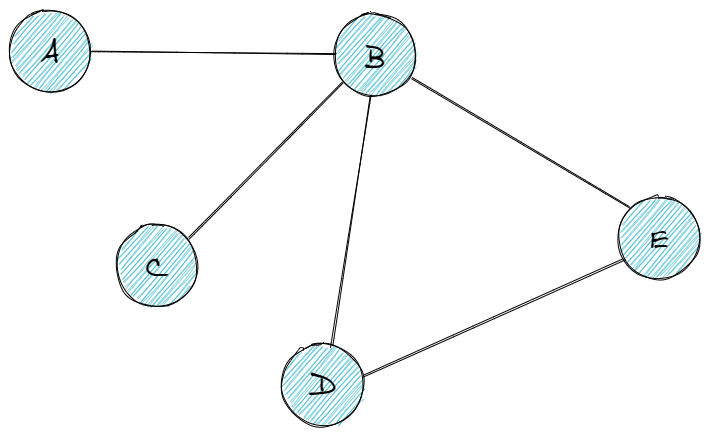
An abstract data type made up of connected vertices and edges that allows operations on those connections.

Section Menu
How do I use this section?

Cheat Sheet
- Quick summary: a data structure that stores items in a connected, non-hierarchical network.
- Important facts:
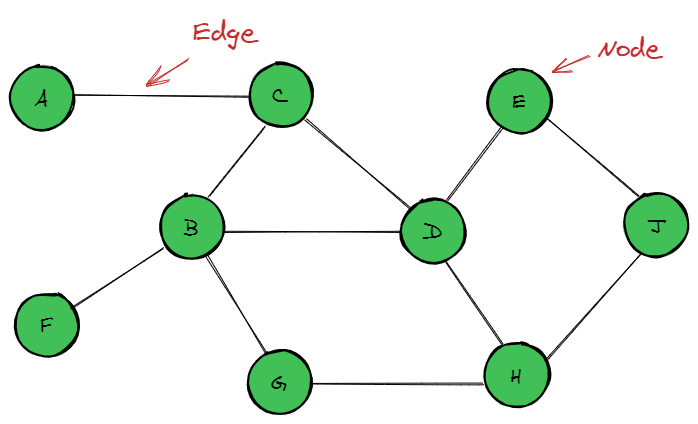
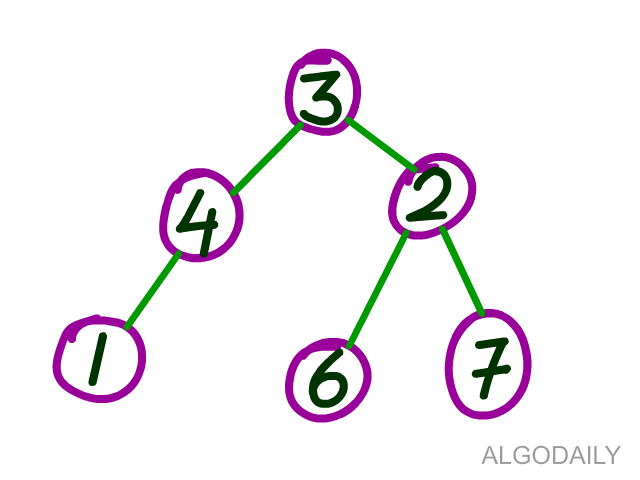
- Each graph element is called a node, or vertex.
- Graph nodes are connected by edges.
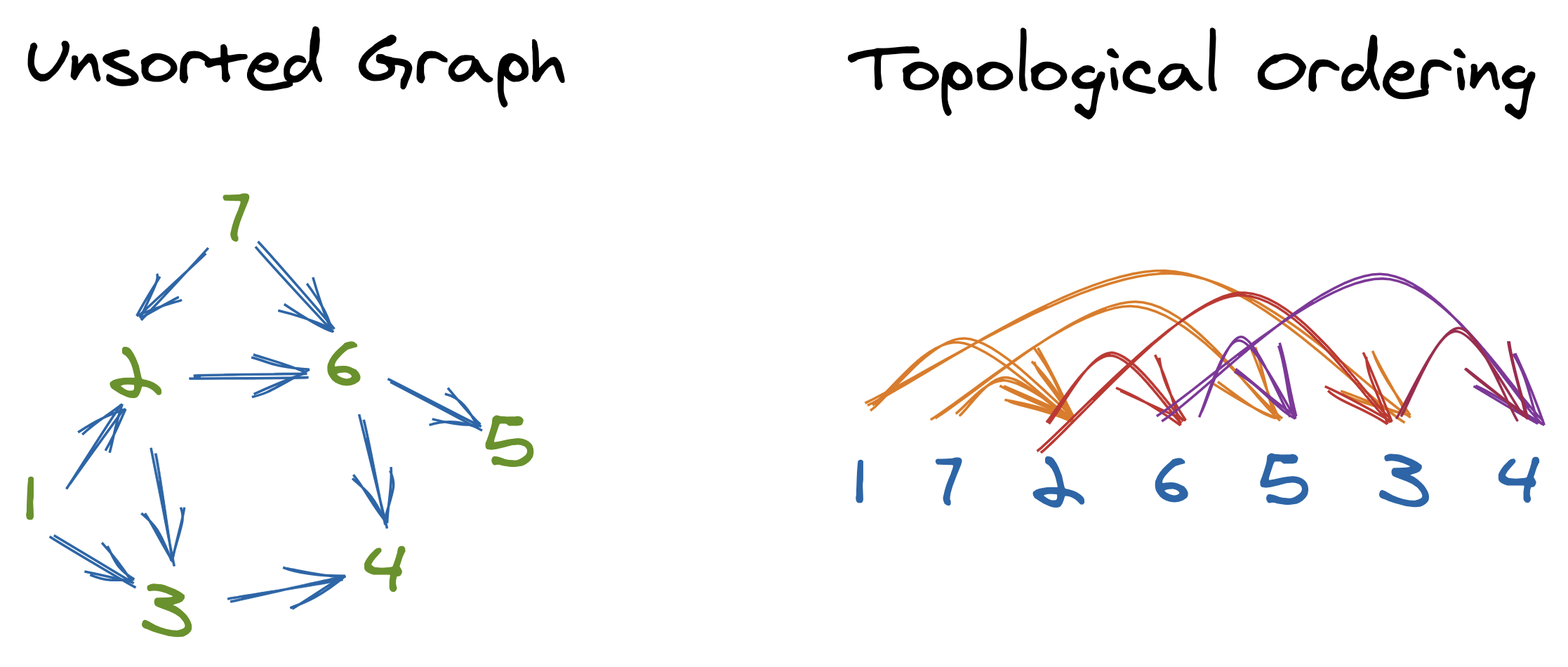
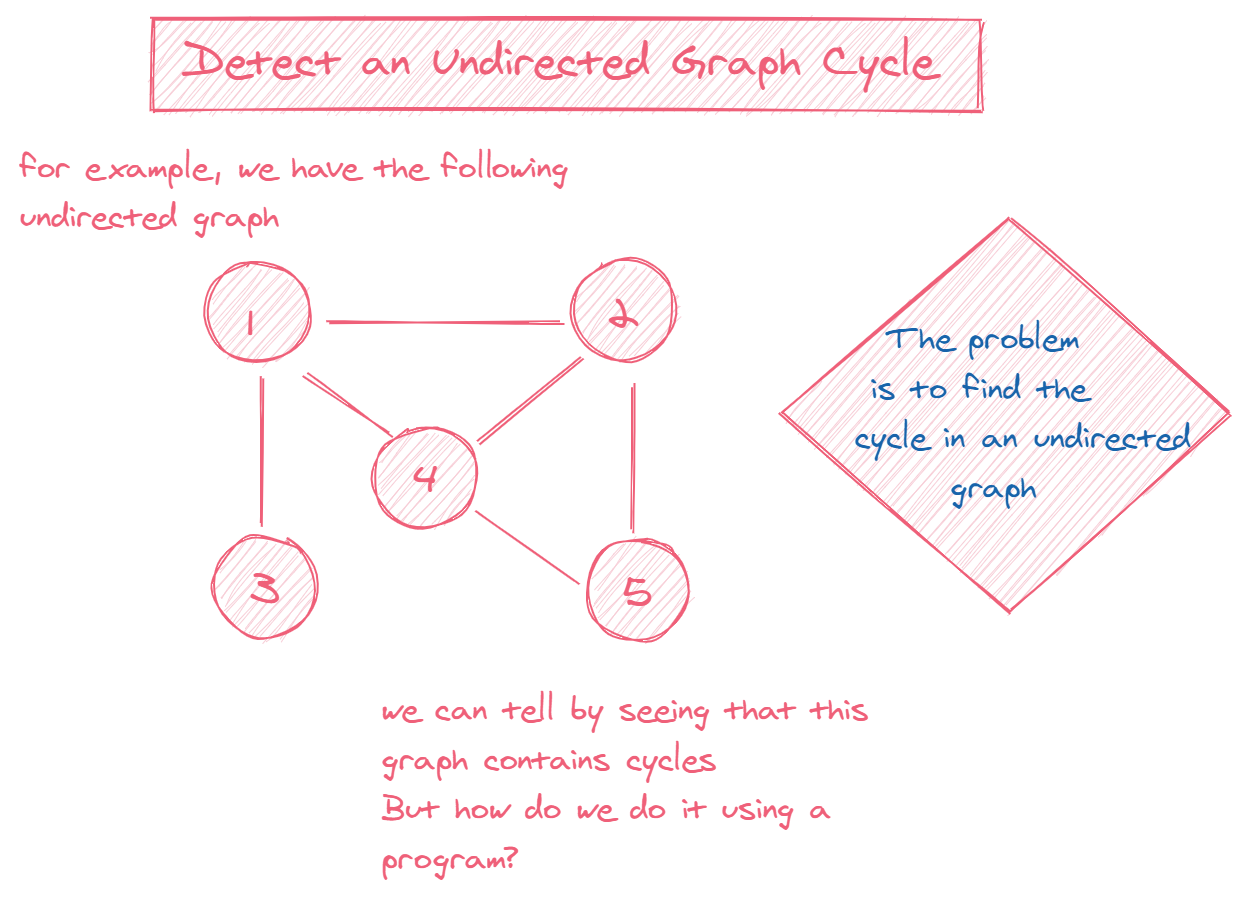
- Graphs can be directed or undirected.
- Graphs can be cyclic or acyclic. A cyclic graph contains a path from at least one node back to itself.
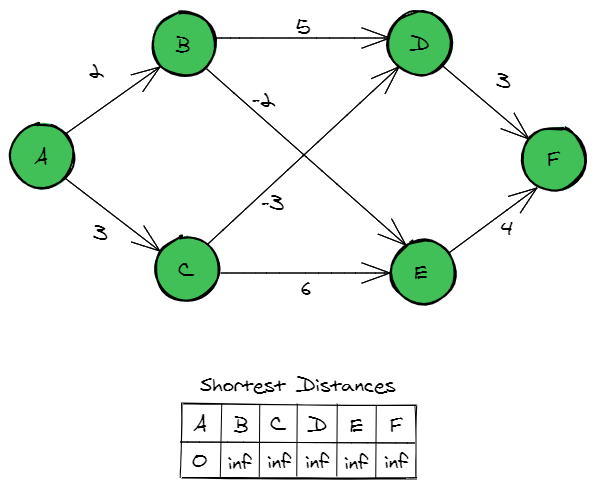
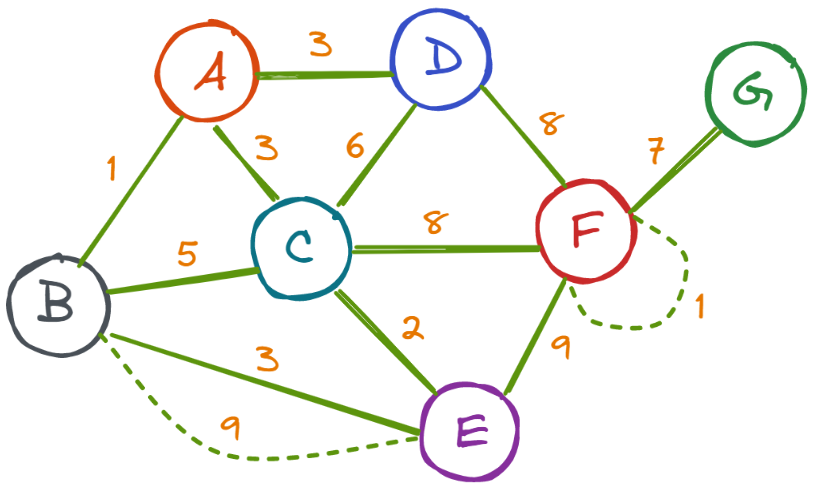
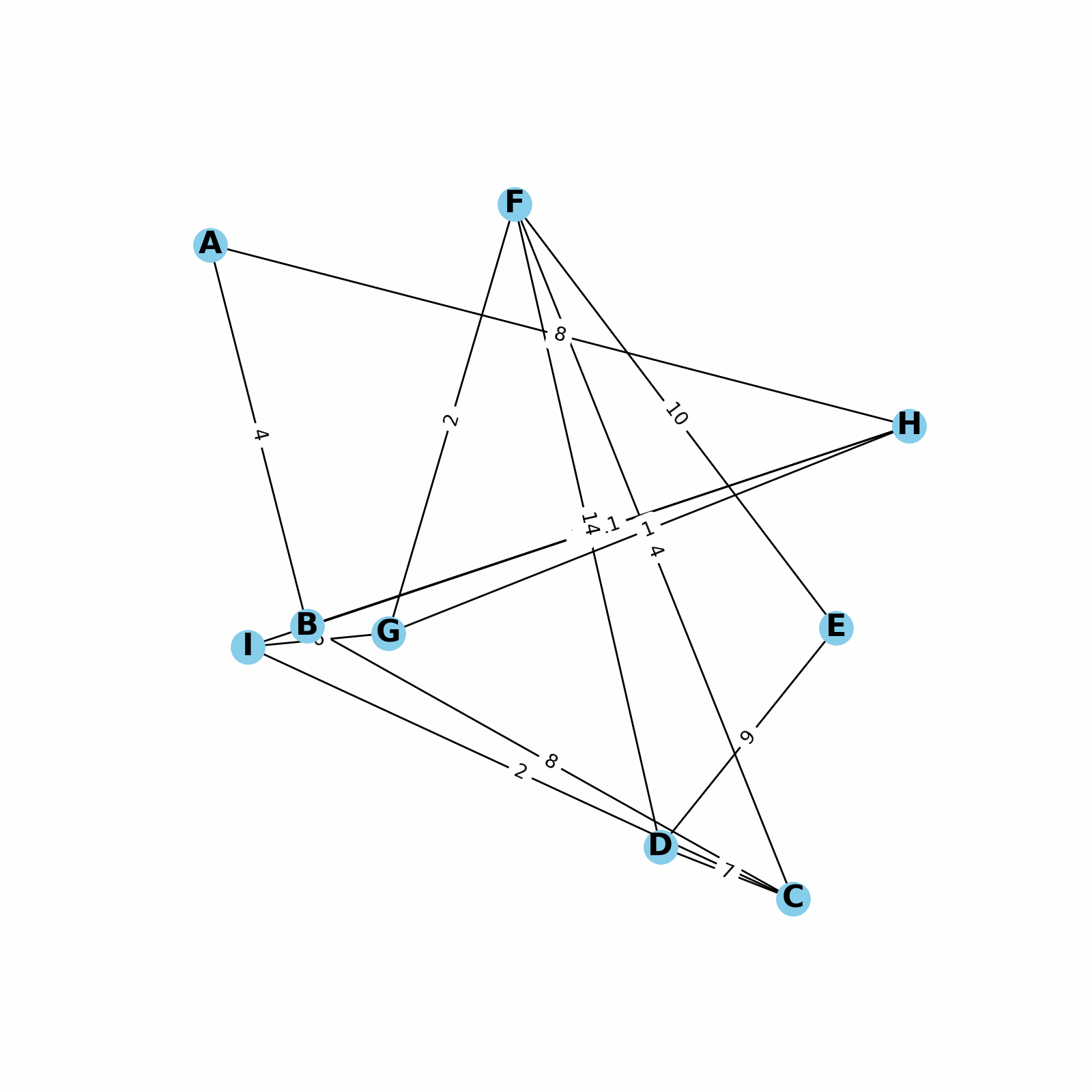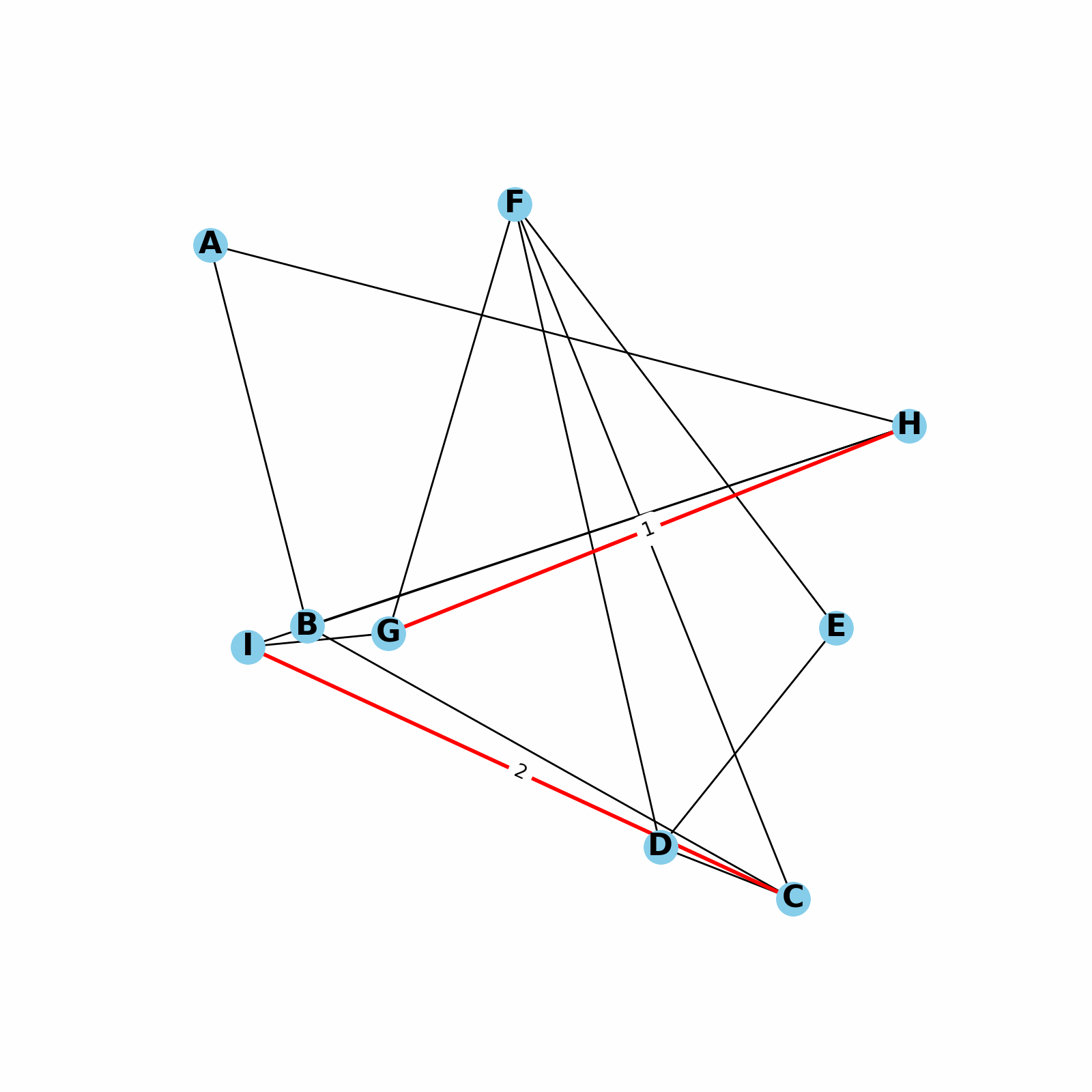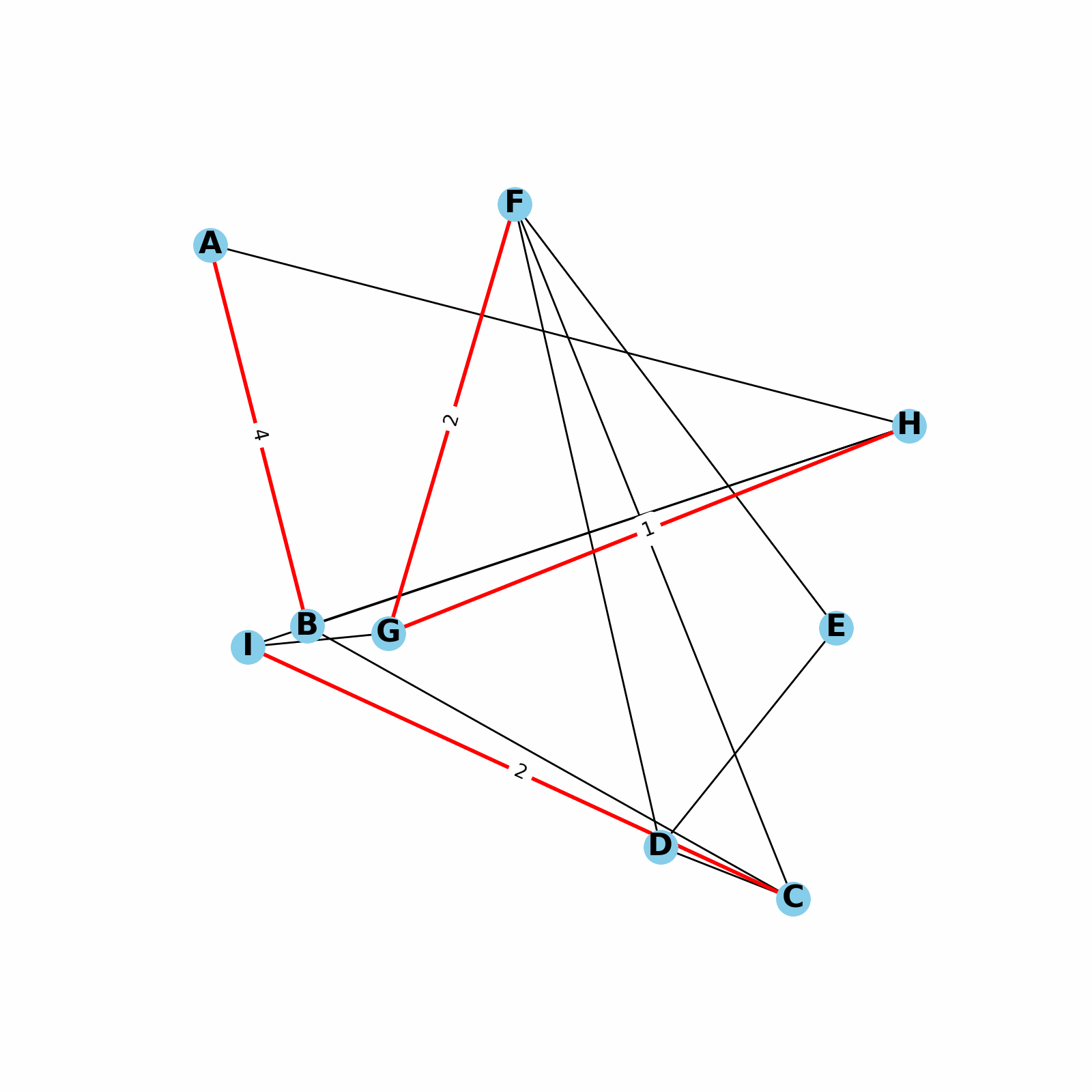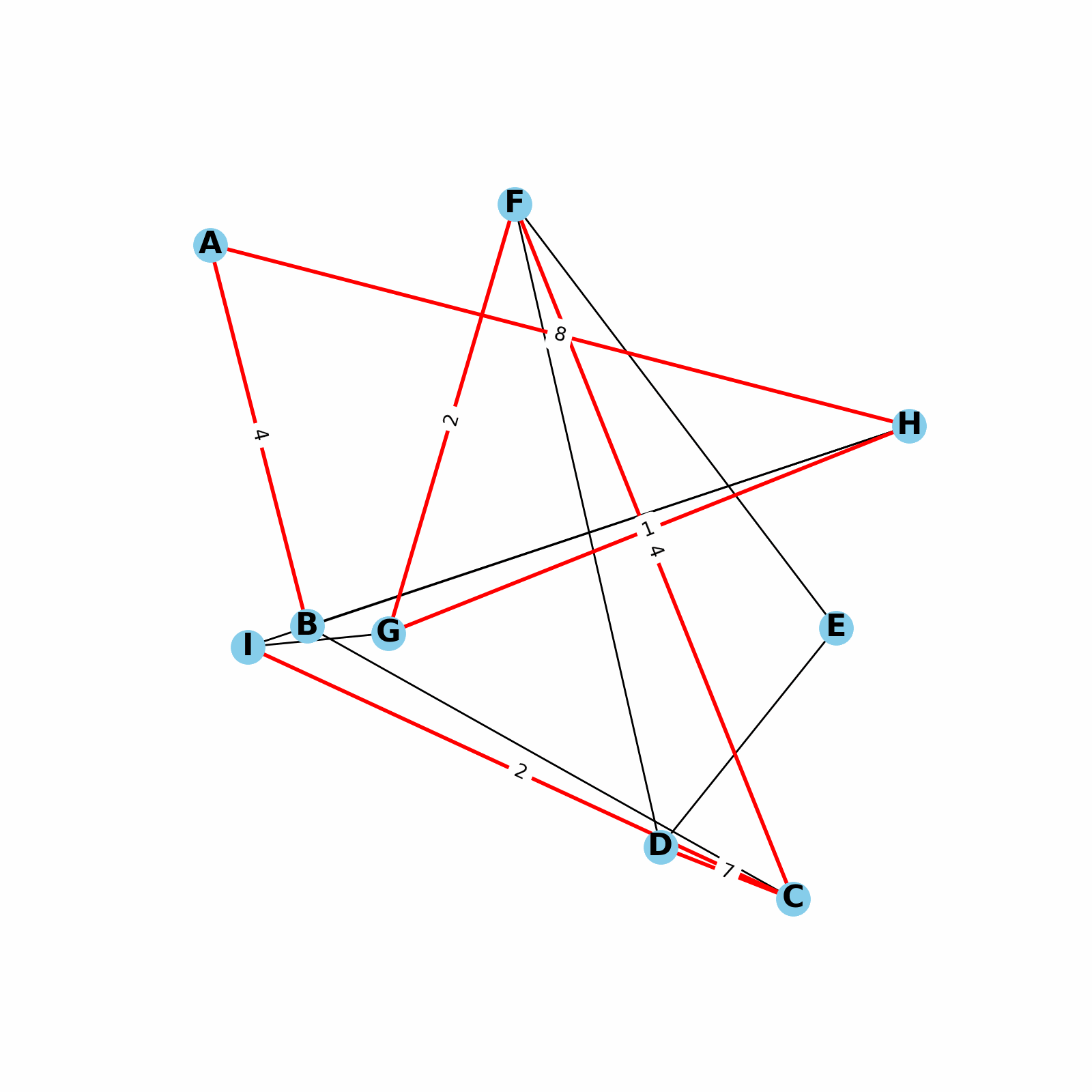
- Graphs can be weighted or unweighted. In a weighted graph, each edge has a certain numerical weight.
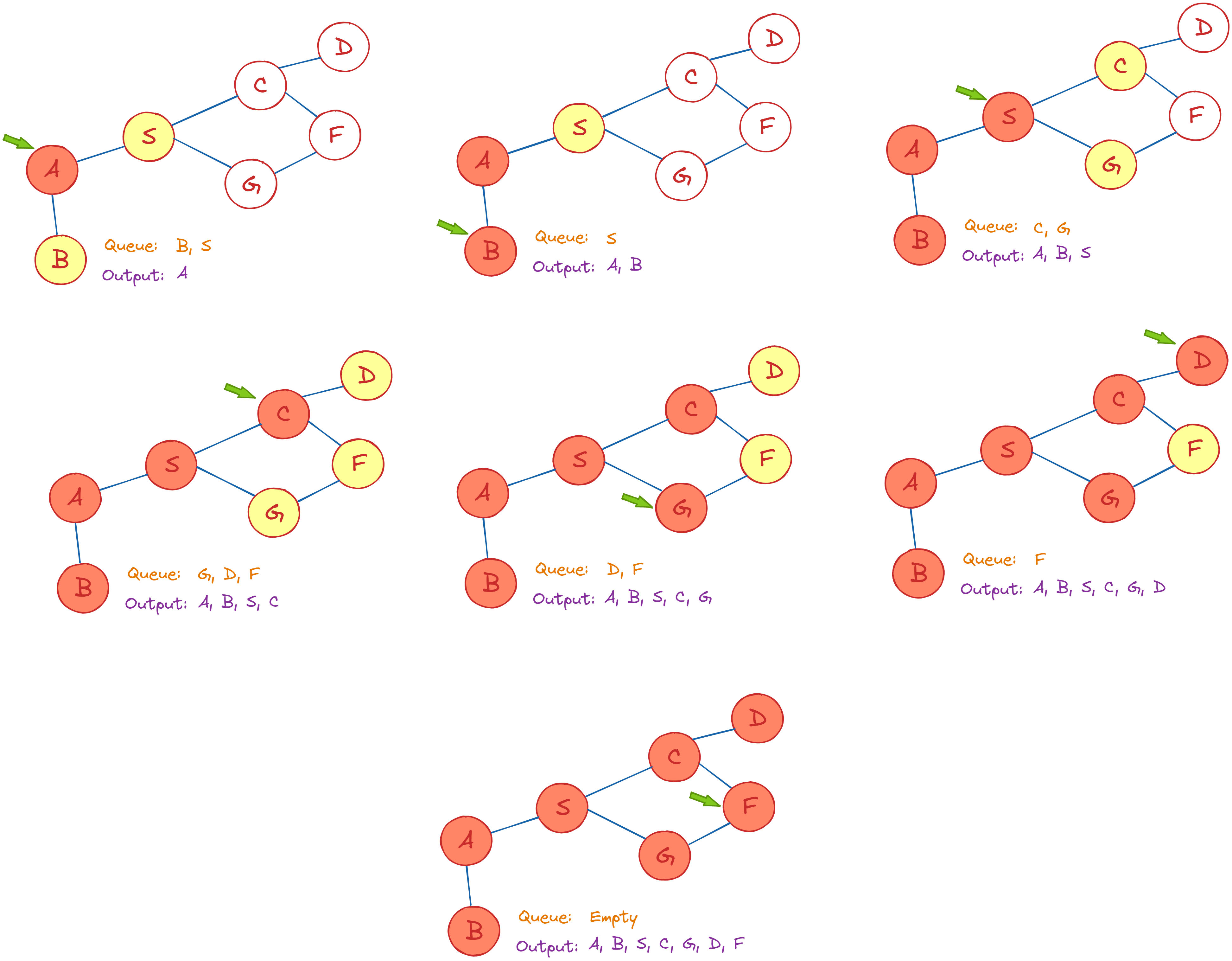
- Graphs can be traversed. See important facts under Tree for an overview of traversal algorithms.
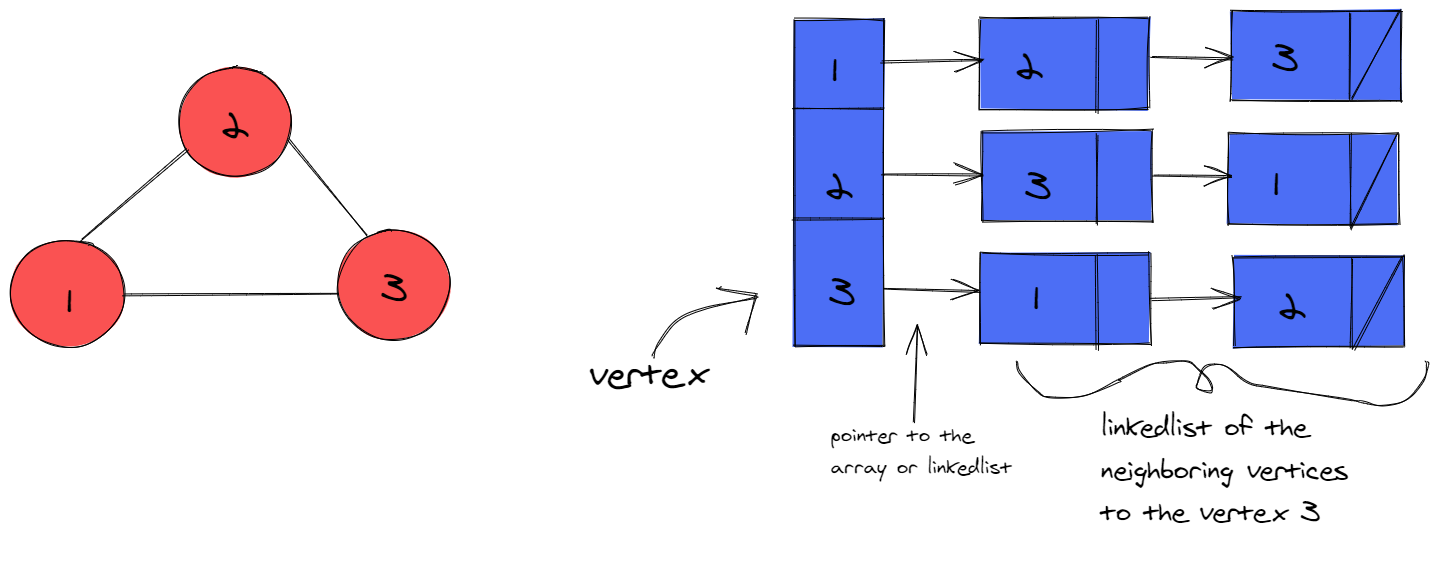
- Data structures used to represent graphs:
- Edge list: a list of all graph edges represented by pairs of nodes that these edges connect.
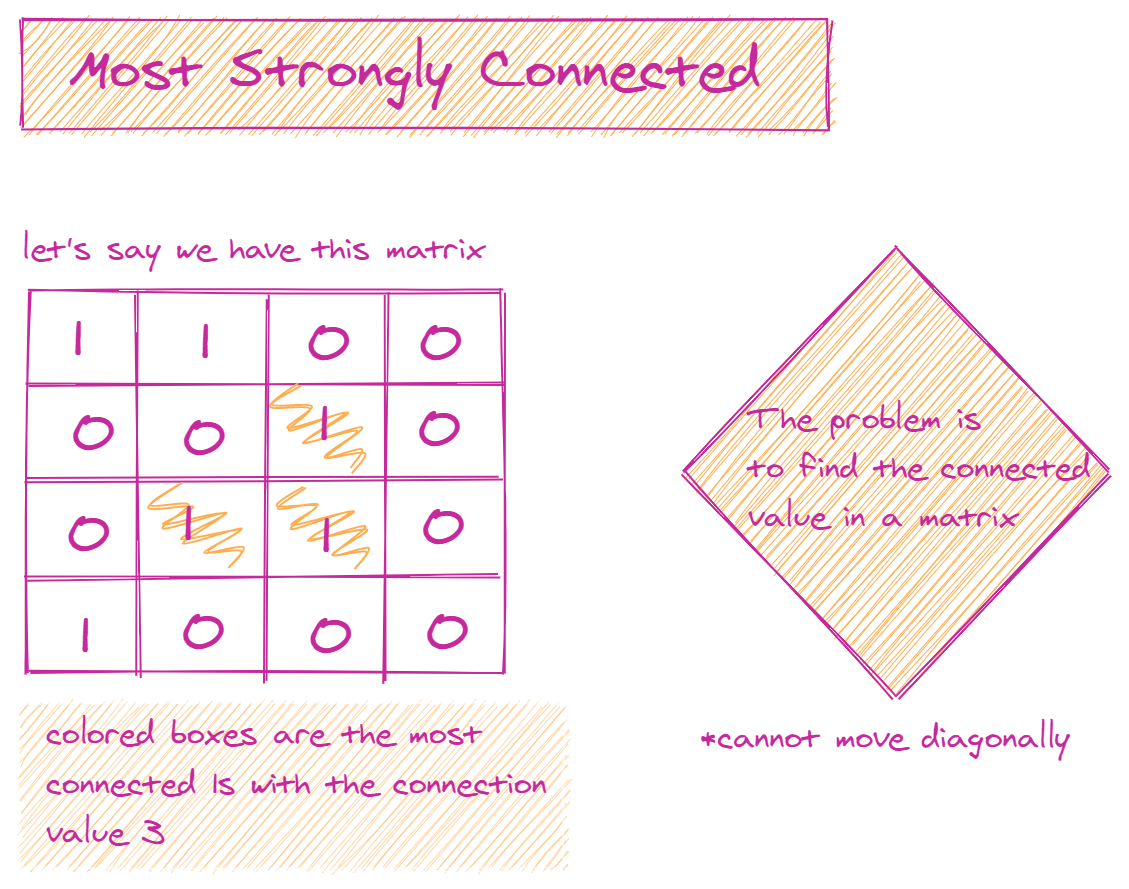
- Adjacency list: a list or hash table where a key represents a node and its value represents the list of this node's neighbors.
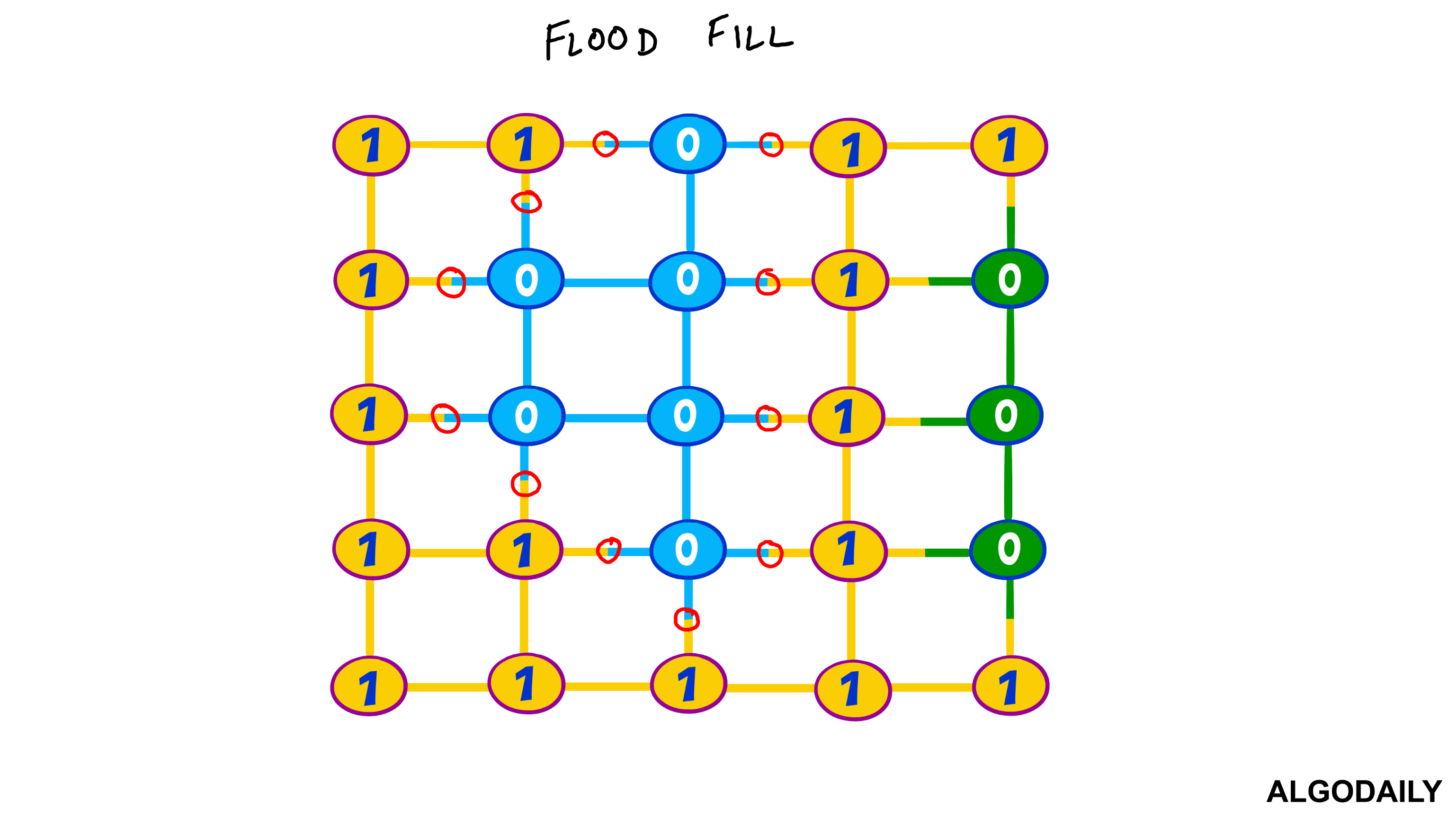
- Adjacency matrix: a matrix of binary values indicating whether any two nodes are connected.
- Pros:
- Ideal for representing entities interconnected with links.
- Cons:
- Low performance makes scaling hard.
- Notable uses:
- Social media networks.
- Recommendations in ecommerce websites.
- Mapping services.
- Time complexity (worst case): varies depending on the choice of algorithm.
O(n*lg(n))or slower for most graph algorithms. - See also: