In this lesson, we are going to learn about the Topological Sort algorithm, one of the most commonly used tree and graph sorting algorithms and techniques for technical interviews.

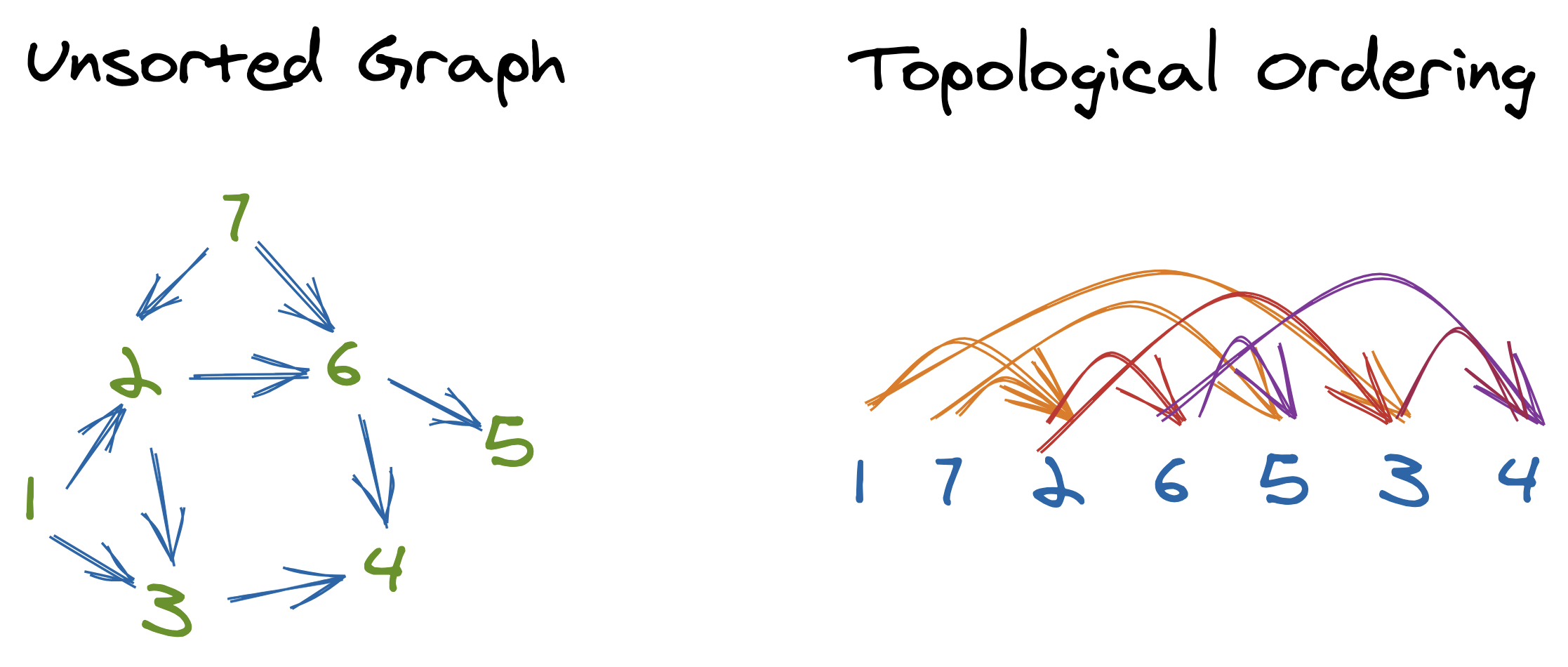
The Essence of Topological Sort

Topological sort is your go-to algorithm for ordering elements in a way that respects their inherent dependencies. Imagine you're a chef with a recipe that must follow certain steps in a particular sequence to whip up a gourmet dish. In the same vein, topological sort gives you a recipe for linearizing nodes in a directed acyclic graph (DAG), commonly used in task scheduling, program compilation, and even solving jigsaw puzzles of dependencies.

Why Do We Need It?

If you have an edge from Node A to Node B (A --> B), Node A must precede Node B in the final list. Think of this as a water flow; water flows in the direction the edges point. So, if you follow the path, you get an idea of who comes before whom.

The Two Golden Rules for Topological Sorting

1. The Graph Must Be Acyclic: In a circle dance, everyone follows everyone, and there's no start or end. A graph that forms a loop is similar. You cannot apply topological sorting to cyclic graphs.

2. The Graph Must Be Directed: Directionality matters. Like one-way streets in a city, the edges of the graph guide you where to go next.

Digging Deeper into Topological Sort

Suppose we have a graph that represents tasks and their dependencies:

1        B ----> C
2       /         ^  
3A --> B         /
4     \         /
5      --> D --

A sensible order to tackle these tasks would be A, B, D, C. This sequence meets all dependency requirements:

• A comes before B
• B comes before both C and D

How It Works: A Simple Guide

1. Initialize: Start by picking any node without incoming edges.
2. Visit Node: Once you pick a node, visit all its neighbors.
3. Check Dependencies: Ensure all incoming dependencies for a neighbor node are visited before you move to it.
4. Add to List: After all dependencies for a node are satisfied, add it to the sorted list.
5. Recursion or Loop: Continue this process recursively or iteratively until all nodes are visited.

Time Complexity

The algorithm takes O(N+E) time, where N is the number of nodes and E is the number of edges. This is achieved through depth-first search (DFS), which is like exploring a maze by going as far as possible before backtracking.

When Topological Sort Fails

Should you encounter a cycle, the algorithm breaks down. In our chef analogy, it's like being told to add salt before boiling water and to boil water before adding salt. Confusing, isn't it?

The Bigger Picture

Topological sorting is your organizational best friend for tasks that require following certain rules or steps in sequence. From scheduling university courses to building skyscrapers, it's an invaluable tool for making sense of complex relationships and dependencies.

The topological sort technique is best explained with the help of an example.

Suppose we have the following graph and want to apply topological sorting to it:

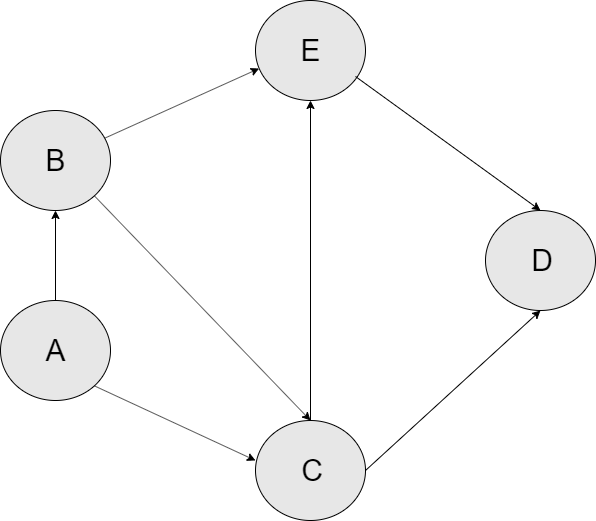
The following steps are required to be performed in order to sort the above graph.

1. The first step is to find the node that has no indegree.

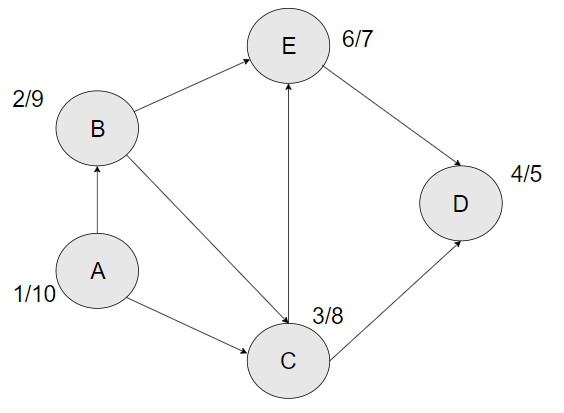
An indegree refers to the number of incoming edges to a node. In the above graph, node A has an indegree of zero, and thus we will start from it. The time step (our record of the order) at which node A is iterated upon will be 1.

2. Node A has an outgoing edge to nodes B and C. Though you can select any node, let's stick alphabetical order for convenience. Node B is visited at time step 2.

3. From node B, we can again visit two nodes (C and E), but let's stick to alphabetical order again. Mark node C as visited at time step 3.

4. The next node will be node D visited at time step 4.

5. Node D has no outgoing edges, so we can mark node D as finished at time step 5.

6. From Node D we will move back to the predecessor node (node C). From node C, we have the outgoing edges to nodes D and E, but since node D is already visited, we will instead move on to node E and mark it as visited at step 6.

7. Node E has only one outgoing edge to node D but it has already been visited. Therefore, Node E will be marked as finished at time step 7, and we will move back to node C.

8. Node C has two outgoing edge to nodes D and E but since both Nodes have been visited, Node C will be marked as finished at time step 8 and we will move back to node A.

9. The outgoing nodes from node B have been visited therefore node B will be marked as finished at time step 9.

10. Finally, Node A will be marked as finished at time step 10 since nodes C and B have been visited already.

The following figure contains the nodes with visited time steps for each node in the numerator and the finished time step for each node in the denominator.

To linearly sort the nodes, arrange the nodes in the descending order of the finished time steps as shown below:

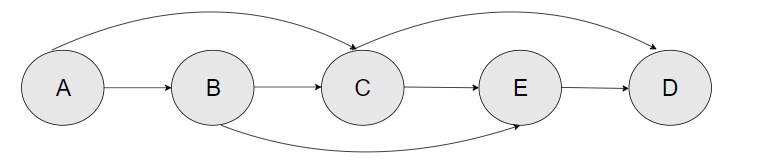
This technique is best used for scheduling tasks or to specify preconditions for a specific task.

For example, consider the above nodes as the names of different courses. We can use a topological sort to specify that you need to take course B and C before you can take course E.

The output of the script above is as follows:

1[1, 2, 3, 5, 4]

The given code is an implementation of topological sorting using Depth First Search (DFS). Topological sorting is used for directed graphs to linearly order the vertices such that for every directed edge ( (u, v) ), vertex ( u ) comes before vertex ( v ) in the ordering. This can be used for scheduling tasks, constructing build systems, and other applications where dependencies must be resolved in a specific order.

Here's a step-by-step explanation of how the code works:

1. Initialization: The code initializes three main data structures:

   • adjacentNodes: An array of lists to represent the adjacency list of the graph.
   • visitedNodes: An array of boolean values to keep track of visited nodes during traversal.
   • sortedNodes: A list to store the nodes in the order they are processed.

2. Creating Edges: The createEdge function is used to create edges between nodes. It takes two nodes (nodeA and nodeB) as input and adds nodeB to the adjacency list of nodeA.

3. Depth First Search (sortArr function):

   • It marks the given node as visited by setting visitedNodes[node] to true.
   • Then, it iterates through all the adjacent nodes of the current node. If an adjacent node is not visited, the function is recursively called with that adjacent node.
   • Finally, the current node is added to the sortedNodes list.

4. Main Loop: The main function initializes the graph structure and calls the sortArr function for each node that has not been visited. This ensures that all connected components of the graph are considered.

5. Reversing the Order: Since the nodes are added to the sortedNodes list in the reverse order of the topological sort, the code reverses the order of sortedNodes to obtain the correct topological order.

6. Printing the Result: Finally, the code prints the sorted nodes, excluding the last item. The exclusion of the last item is specific to the given code and may be related to the input graph structure.

Note: This code assumes that the graph doesn't contain any cycles. If there are cycles, topological sorting is not possible, and the code would need to include mechanisms to detect and handle cycles.

One Pager Cheat Sheet

• The main objective of this lesson is to teach about Topological Sort and its use for programming interviews and challenges.
• A topological sort is a sorting technique used to linearly arrange the nodes in an acyclic, directed graph or tree based on the order the edges point.
• Topological sorting is an ordered approach to visiting the vertices of a Directed Acyclic Graph that follows the direction of its edges.
• A DAG (Directed Acyclic Graph) has no cycles so it can be used for Topological Sorting, allowing for the linear ordering of its vertices.
• By following a specific order of visiting nodes with no incoming edges and consecutively marking them as visited/finished, we can topologically sort a given graph.
• To arrange the nodes linearly in a descending order of their finished time steps is called Topological Sort, which is best used for scheduling tasks or specifying preconditions for a specific task.
• This topological sort can be implemented using Python.
• The output of the script is presented below.