The topological sort technique is best explained with the help of an example.

Suppose we have the following graph and want to apply topological sorting to it:

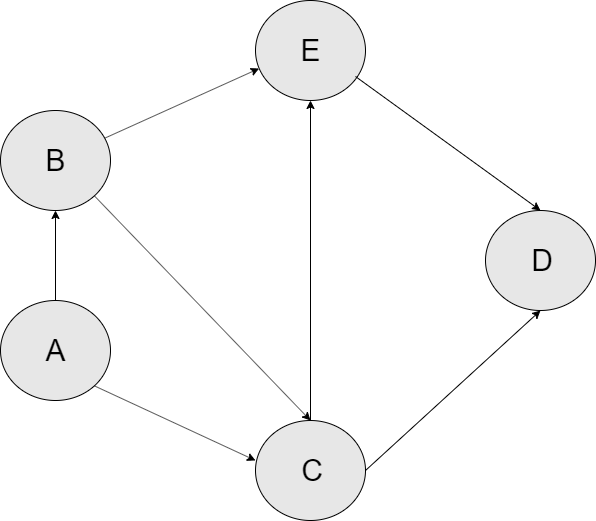
The following steps are required to be performed in order to sort the above graph.

1. The first step is to find the node that has no indegree.

An indegree refers to the number of incoming edges to a node. In the above graph, node A has an indegree of zero, and thus we will start from it. The time step (our record of the order) at which node A is iterated upon will be 1.

2. Node A has an outgoing edge to nodes B and C. Though you can select any node, let's stick alphabetical order for convenience. Node B is visited at time step 2.

3. From node B, we can again visit two nodes (C and E), but let's stick to alphabetical order again. Mark node C as visited at time step 3.

4. The next node will be node D visited at time step 4.

5. Node D has no outgoing edges, so we can mark node D as finished at time step 5.

6. From Node D we will move back to the predecessor node (node C). From node C, we have the outgoing edges to nodes D and E, but since node D is already visited, we will instead move on to node E and mark it as visited at step 6.

7. Node E has only one outgoing edge to node D but it has already been visited. Therefore, Node E will be marked as finished at time step 7, and we will move back to node C.

8. Node C has two outgoing edge to nodes D and E but since both Nodes have been visited, Node C will be marked as finished at time step 8 and we will move back to node A.

9. The outgoing nodes from node B have been visited therefore node B will be marked as finished at time step 9.

10. Finally, Node A will be marked as finished at time step 10 since nodes C and B have been visited already.