Home > Data Structures and Algorithms 🚀 > Draw a Graph > What Is The Manhattan Distance?

What Is The Manhattan Distance?

The Manhattan Distance is used to calculate the distance between two coordinates in a grid-like path.

Imagine you are on holidays in New York City, you are visiting the Empire State Building and decide to walk to The Morgan Library & Museum by the route below. From the map it is easy to see why Manhattan Distance is also known as city block distance or taxicab geometry.

Unlike the green line from the picture we cannot walk directly to the destination since we are constrained to the city's coordinate axes, therefore we would follow something more similar to the red line.

Manhattan Distance Formula: A Stroll Through the City Grid

Imagine you're a tourist in New York City, and you have to walk from the Empire State Building to another famous landmark. If you've ever been to a city with a grid system, like Manhattan, you'll notice that you can't always walk diagonally through buildings (unlike birds who can fly in a straight line). Instead, you walk along streets, taking right angles. The Manhattan Distance is a measure of the distance you'd walk, not the straight line or "as-the-crow-flies" distance.

Visualizing the Route

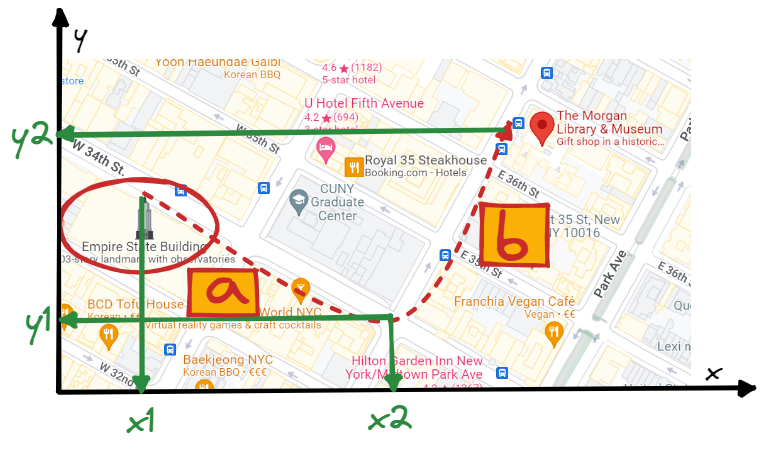
In the illustration above, the distance from the Empire State Building to the first corner is the horizontal distance. It's computed by the difference in the x-coordinates: |x_2 - x_1|. Likewise, the vertical distance, from the corner to the destination, is |y_2 - y_1|. By summing up these distances, we get the total Manhattan distance.

Why the Absolute Value?

The absolute value ensures that the distance is always positive, regardless of the direction. Think about it: If you were to walk 5 blocks north or 5 blocks south, the effort (or distance) is the same. It's 5 blocks!

Formalizing the Formula

Given two points (x_1, y_1) and (x_2, y_2), the Manhattan Distance d between them is:

d = |x_1 - x_2| + |y_1 - y_2|

When it comes to vectors, the formula can be expanded:

d = Σ|A_i – B_i|

Where:

A and B are vectors.
i represents the i^{th} element in each vector.

Manhattan Distance in Machine Learning

In machine learning, the Manhattan distance is often used in clustering algorithms or when we need a distance metric between two datasets. For example, it's used in the K-Nearest Neighbors algorithm to find data points that are "close" to a given point.

Code to Compute Manhattan Distance

To make our life simpler, Python provides libraries that readily compute this for us. When you run the code, it will display:

SNIPPET

1Output: Manhattan Distance between [2, 4, 4, 6] and [5, 5, 7, 8] is 9

This means that if these vectors were points in a city, you'd have to walk 9 blocks to get from point A to point B!

xxxxxxxxxx
 
// Define two vectors
const A = [2, 4, 4, 6];
const B = [5, 5, 7, 8];
​
// Calculate Manhattan Distance between the vectors
function cityBlockDistance(vec1, vec2) {
    if (vec1.length !== vec2.length) {
        throw new Error("Vectors must be of the same length");
    }
    let sum = 0;
    for (let i = 0; i < vec1.length; i++) {
        sum += Math.abs(vec1[i] - vec2[i]);
    }
    return sum;
}
​
const manhattanDistance = cityBlockDistance(A, B);
console.log(`Manhattan Distance between ${A} and ${B} is ${manhattanDistance}`);

Build your intuition. Is this statement true or false?

Manhattan Distance is also known as city block distance.

Press true if you believe the statement is correct, or false otherwise.

Build your intuition. Click the correct answer from the options.

Calculate the Manhattan distance between the vectors C (3,2,5) and D (4,1,7).

Click the option that best answers the question.

Understanding Manhattan Distance: Beyond the City Blocks

Manhattan Distance, often referred to as "L1 distance" or "Taxicab" or "City block" distance, is grounded in a fascinating blend of geometry and real-world practicality. Let's further unravel this concept.

Historical Origins

The name "Manhattan Distance" comes from the grid layout of the streets in Manhattan, which is one of the boroughs of New York City. When you travel from one point to another in Manhattan, you can't go directly if buildings are in the way. Instead, you have to navigate the grid, moving horizontally and vertically, much like taxis do. Hence, the distance traveled is not the direct route (as a bird might fly) but is instead the sum of the horizontal and vertical distances.

Mathematical Perspective

From a geometric perspective, the Manhattan distance is the distance between two points measured along axes at right angles. In a plane with p_1 = (x_1, y_1) and p_2 = (x_2, y_2), it is |x_1 - x_2| + |y_1 - y_2|.

However, the concept extends beyond 2 dimensions. In an n-dimensional space, the Manhattan distance between two points P and Q is:

$d (P, Q) = \sum_{i = 1}^{n} | p_{i} - q_{i} |$

Applications

Computer Vision: Manhattan distance can be used in image processing to compare the similarity between two images or shapes. For instance, it helps in contour matching, where the goal is to find the best match for a contour from a set of contours.
Games: In games like Chess or the 8-puzzle, Manhattan distance can be used as a heuristic to estimate the minimum number of moves required to reach the target state from a given state.
Robotics: Robots, especially those moving in grid-like environments, can use Manhattan distance to estimate paths and distances to targets.
Economics: In economic geography, the concept is applied to measure the shortest path that consumers take to reach a given facility.

Advantages over Euclidean Distance

Computationally Faster: In environments where direction can only be changed on a grid (like streets in a city), Manhattan distance is computationally faster to calculate than the Euclidean distance.
Less Sensitive to Outliers: Manhattan distance, due to its nature of calculation, can sometimes be less sensitive to outliers than Euclidean distance.

Drawbacks

Not always the Shortest Path: Especially in non-grid environments, Manhattan distance might not represent the most efficient path.
Over-simplification: In many real-world scenarios, there might be other obstacles or considerations, making the Manhattan estimate too simplistic.

Conclusion

Manhattan Distance is the sum of the absolute differences between two vectors. Distance measures play an important role in Machine Learning. Manhattan Distance is preferred over the Euclidean distance metric as the dimensions of the data increases.

One Pager Cheat Sheet

The Manhattan Distance, also known as city block distance or taxicab geometry, calculates the distance between two coordinates in a grid-like path, similar to pathways on a city map, rather than a direct line.
The Manhattan Distance, measured along grid-like city blocks, is calculated using the formula ( d = |x_1 - x_2| + |y_1 - y_2| ) and is implemented in machine learning (especially in clustering algorithms, such as the K-Nearest Neighbors) and other applications where a distance metric between two datasets or vectors is needed, with libraries in languages like Python (particularly the cityblock function from the scipy.spatial.distance library) simplifying the process.
The Manhattan Distance, also known as city block distance, measures the total distance traveled along a grid by calculating the combined horizontal and vertical distance covered, mimicking navigation in a city built on a grid system.
The Manhattan distance between two vectors C (3,2,5) and D (4,1,7) is calculated by summing the absolute differences of their coordinates, resulting in a Manhattan Distance of 4.
The Manhattan Distance, also known as "L1 distance" or "Taxicab" or "City block" distance, originated from the grid-like street layout of Manhattan, is a geometric concept that calculates the total horizontal and vertical distances between two points, and has diverse applications in fields including computer vision, games, robotics, and economics.
The Manhattan Distance, which is the sum of the absolute differences between two vectors, is crucial in Machine Learning and preferred over the Euclidean distance metric as the dimensions of the data increase.