Good morning! Here's our prompt for today.

You're given an array of multiple sorted linked lists. Can you write a method that returns it transformed into a single sorted linked list?

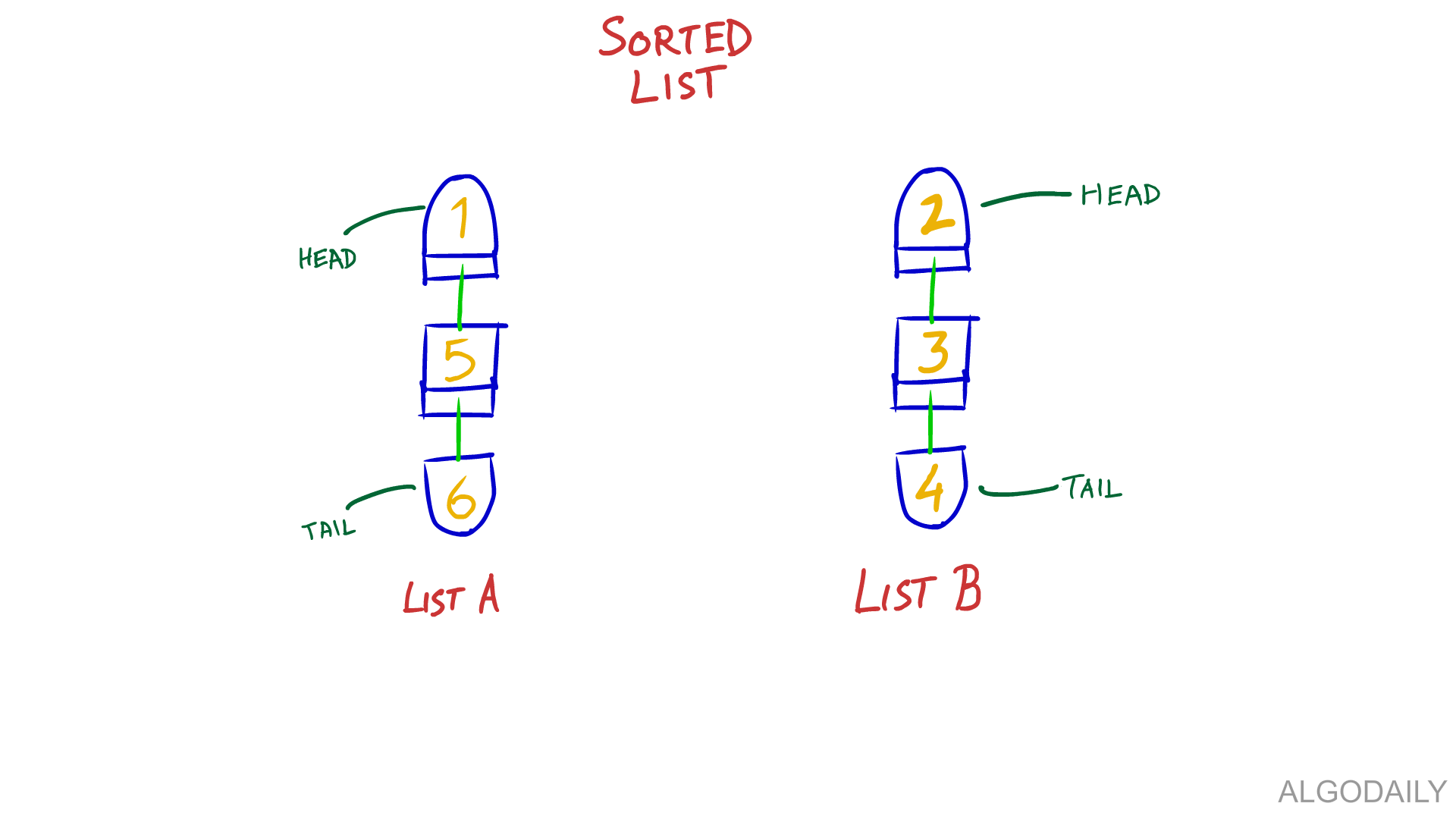
Each linked list can be represented as a series of nodes with the following definition:

1function Node(val) {
2  this.value = val;
3  this.next = null;
4}

Here's how it would be invoked:

1// Input
2const arr = [
3  2 -> 6 -> 9,
4  1 -> 2 -> 7,
5  2 -> 6 -> 10
6]
7
8mergeLists(arr);
9
10// Output
111 -> 2 -> 2 -> 2 -> 6 -> 6 -> 7 -> 9 -> 10

Constraints

• Each list can have up to 100000 nodes
• The cumulative sum of all the nodes in the linked lists will be <= 100000
• The values in the nodes will be in the range -1000000000 and 1000000000
• Let n and k be the length of a linked list and number of lists
• Expected time complexity : O(n*k*log k)
• Expected space complexity : O(k)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

​

def merge_lists(arr):

    # fill in

    return arr[0]

​

​

# Node definition

class Node:

    def __init__(self, val):

        self.val = val

        self.next = None

​

​

def create_nodes(head, nodes):

    for val in nodes:

        new_node = Node(val)

        head.next = new_node

        head = new_node

​

​

list1 = Node(3)

nodes1 = [4, 5, 6, 7, 8, 9, 10]

create_nodes(list1, nodes1)

​

list2 = Node(1)

nodes2 = [2, 3, 4, 5, 6, 7, 8]

create_nodes(list2, nodes2)

​

​

def list_to_str(head):

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

This is a more difficult problem than it may initially seem!

An obvious brute force solution is simply to:

1. Traverse through every list
2. Store all the node values in an array
3. Sort the array. Unfortunately here, the time complexity is O(n log n) since there are n total nodes and sorting takes O(n log n) time.

We can improve on the brute force approach by instead comparing node to node, and putting them in the right order as we're traversing. This becomes very similar to the Merged Sorted Linked Lists problem.

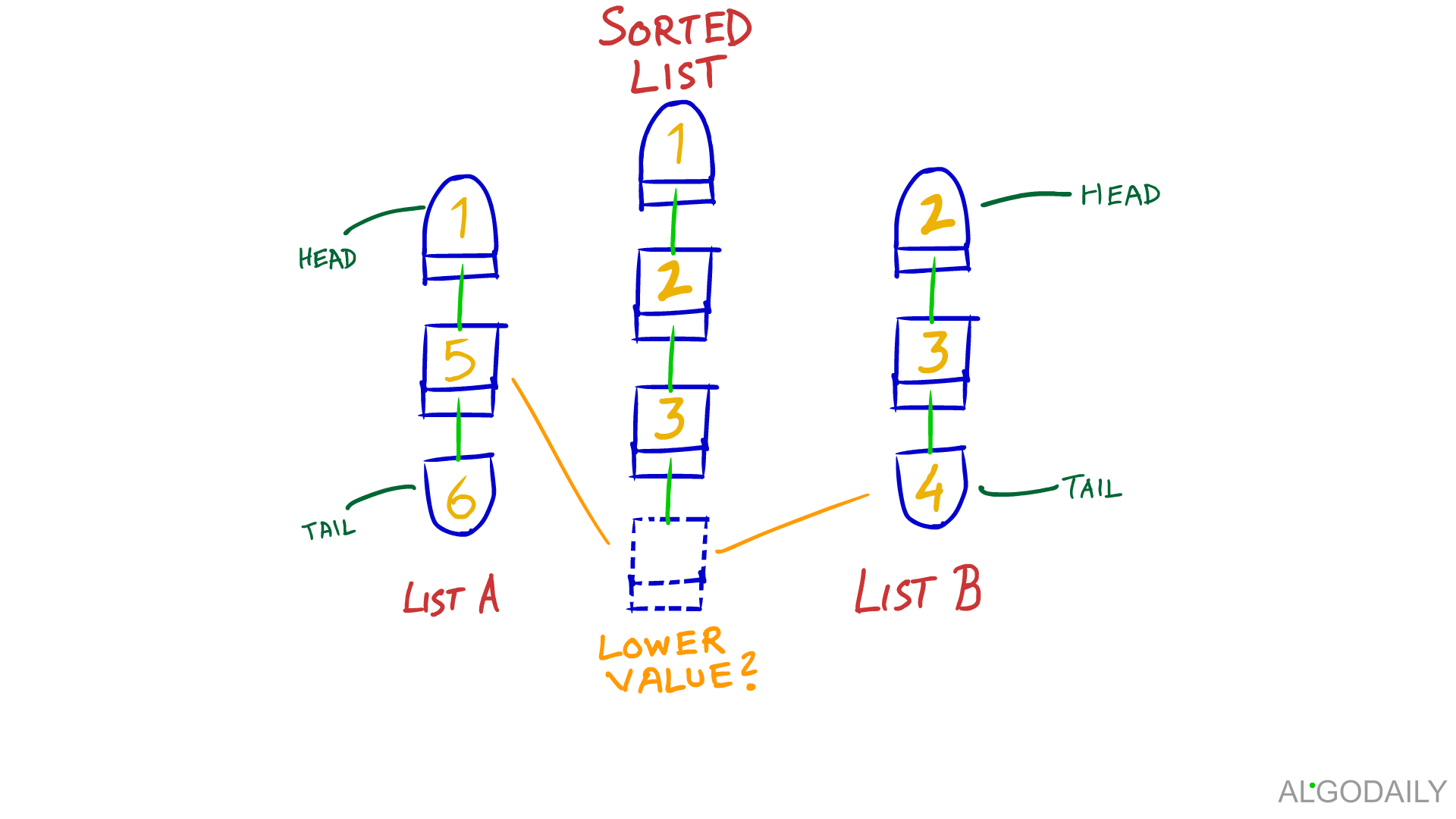
A better approach is to introduce a data structure. We need something that is built to process and order elements one by one in an efficient manner. What about a priority queue?

A priority queue is an abstract data type used to maintain a queue, with each element having a concept of a priority or order to be served.

Let's start by implementing one with a simple insert method:

xxxxxxxxxx

class PriorityQueue {

  constructor() {

    this.first = null;

    this.size = 0;

  }

​

  insert(val) {

    // decide where in the queue it falls

    const newNode = new Node(val);

    // if there's no first node or this new node is higher priority, move it to first

    if (!this.first || newNode.val < this.first.val) {

      newNode.next = this.first;

      this.first = newNode;

    } else {

      // if it's a lower priority on the queue by value

      let currNode = this.first;

​

      // keep iterating until we find a node whose value we are greater than

      while (currNode.next && newNode.val > currNode.next.val) {

        currNode = currNode.next;

      }

      newNode.next = currNode.next;

      currNode.next = newNode;

    }

  }

}

Then, using it is a matter of running the linked lists through it:

xxxxxxxxxx

let pq = new PriorityQueue();

for (let list of arrOfLists) {

  if (list) {

    let currentNode = list;

    pq.insert(currentNode.val);

​

    // process the rest of the list

    while (currentNode.next) {

      pq.insert(currentNode.next.val);

      currentNode = currentNode.next;

    }

  }

}

​

// returning this will return the head of the priority queue linked list result

return pq.first || [];

Don't forget to handle the case when the array is empty:

xxxxxxxxxx

if (!arrOfLists || arrOfLists.length === 0) {

  return [];

}

Let's put it all together now.