AlgoDaily - Power of Three

Good morning! Here's our prompt for today.

Given an integer num, write a method to determine if it is a power of 3.

The method will be called as follows:

JAVASCRIPT

1console.log(powerOfThree(9));
2// true
3
4console.log(powerOfThree(7));
5// false

Constraints

The given would be a non zero positive integer in the range between 1 and 2147483647
Expected space complexity : O(logn)
Expected time complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
def power_of_three(num):
    # fill in
    return False
​
​
import unittest
​
​
class Test(unittest.TestCase):
    def test_1(self):
        assert power_of_three(9) == True
        print("PASSED: `power_of_three(9)` should be `True`")
​
    def test_2(self):
        assert power_of_three(7) == False
        print("PASSED: `power_of_three(7)` should be `False`")
​
    def test_3(self):
        assert power_of_three(729) == True
        print("PASSED: `power_of_three(729)` should be `True`")
​
​
if __name__ == "__main__":
    unittest.main(verbosity=2)
    print("Nice job, 3/3 tests passed!")
​

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's our guided, illustrated walk-through.

How do I use this guide?

Are you sure you're getting this? Click the correct answer from the options.

In the expression 3^6 what does the ^6 stand for?

Click the option that best answers the question.

The exponent of the expression
The power of the exponent
The square root of the number
The degree of the exponent

Build your intuition. Click the correct answer from the options.

What is a loop in programming terminology?

Click the option that best answers the question.

A declarative program that assigns a permanent address to the program counter
A control structure used to repeat a given section of code until a particular condition is met
An imperative program to determine the arithmetical operator
A conditional statement used only to return the Boolean value of the program counter

Are you sure you're getting this? Fill in the missing part by typing it in.

In programming, the while-loop can be considered as a repeating _ statement.

Write the missing line below.

Try this exercise. Click the correct answer from the options.

Identify the correct exponential expression for the integer 729.

Click the option that best answers the question.

Build your intuition. Is this statement true or false?

In programming, the exponential value of a number cannot be determined without loops.

Press true if you believe the statement is correct, or false otherwise.

The easiest way to go about this is to think about how exponents work. When you see 3^6, you are multiplying 3 by 3 exactly 6 times.

With that said, we can simply reverse the direction: we can take the result, and continuously divide it by 3. If we eventually get to 1, we know that it's been divisible all along and is thus an exponent of 3.

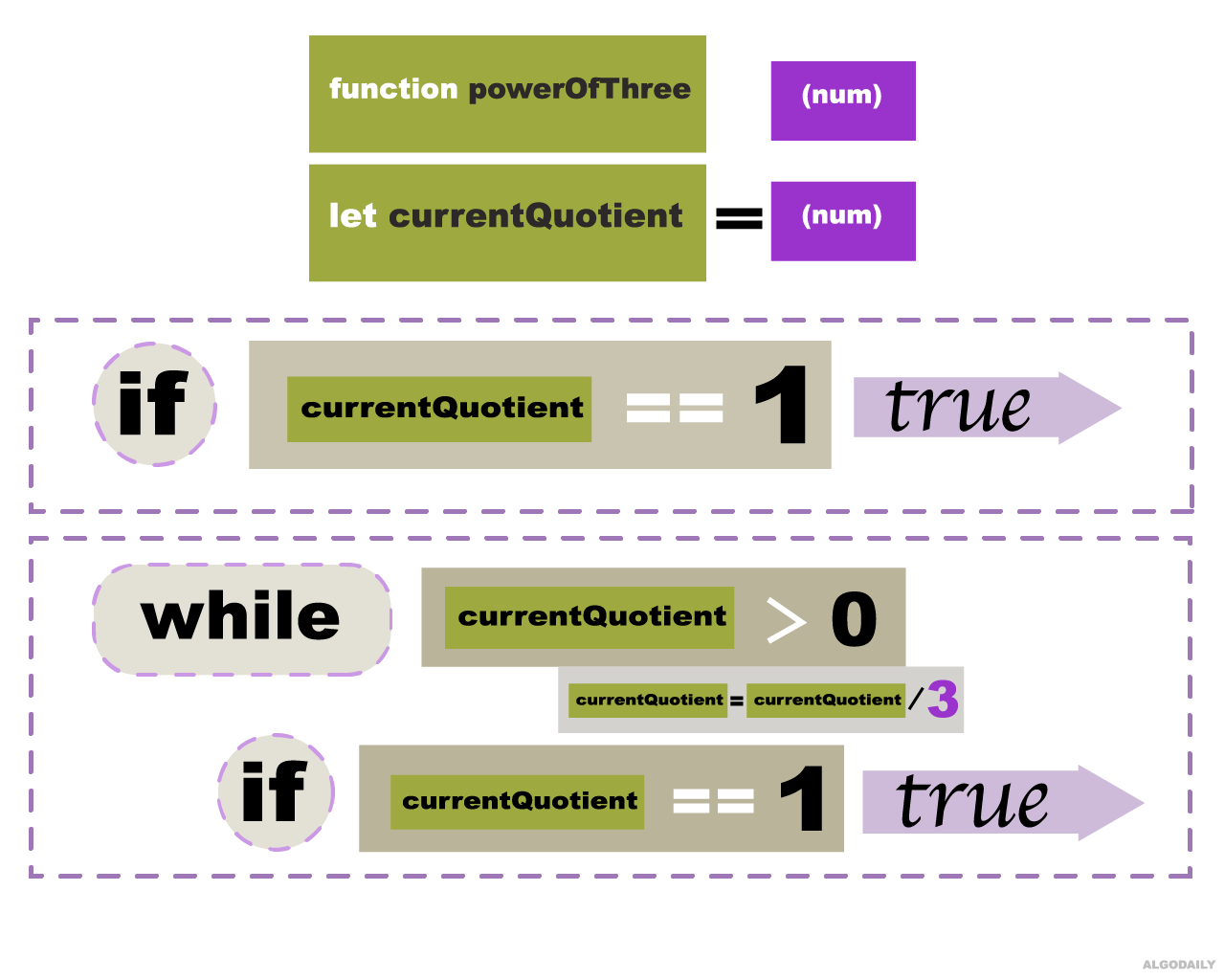
Complexity of Final Solution

Since we are dividing by 3 for every iteration in the while loop, we find our answer after roughly log3(n) (base 3) iterations for O(logn) time complexity. We do not use any additional data structures, so we use O(1) constant space.

One Pager Cheat Sheet

Write a method powerOfThree which determines if a given non zero positive integer num between 1 and 2147483647 is a power of 3, with an expected space complexity of O(logn) and an expected time complexity of O(1).
The ^6 in 3^6 stands for the exponent calculated using the formula base^exponent = result.
Loops are a useful control structure in programming used to repeat certain code multiple times, saving the developer time when dealing with large data sets or unknown iterations.
The while-loop can be considered as a repeating IF-statement because it needs an initial evaluation of the condition before continuing to repeat a certain set of instructions as long as the condition is true.
The number 729 can be expressed using exponential notation as 3^6, since it is the result of raising 3 to the 6th power.
The exponential value of any number can be calculated without loops, simply by raising that number to the power of itself.
We can solve this problem in O(logn) time complexity and O(1) space complexity by continuously dividing the number by 3.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
    print("Nice job, 3/3 tests passed!")
 
def power_of_three(num):
    curr_quotient = num
    if curr_quotient == 1:
        return True
​
    while curr_quotient > 0:
        curr_quotient = curr_quotient / 3
        if curr_quotient == 1:
            return True
​
    return False
​
​
import unittest
​
​
class Test(unittest.TestCase):
    def test_1(self):
        assert power_of_three(9) == True
        print("PASSED: `power_of_three(9)` should be `True`")
​
    def test_2(self):
        assert power_of_three(7) == False
        print("PASSED: `power_of_three(7)` should be `False`")
​
    def test_3(self):
        assert power_of_three(729) == True
        print("PASSED: `power_of_three(729)` should be `True`")
​
​
if __name__ == "__main__":
    unittest.main(verbosity=2)

Great job getting through this. Let's move on.

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Here's a video of us explaining the solution.

Here's our guided, illustrated walk-through.

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Are you sure you're getting this? Fill in the missing part by typing it in.

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

Build your intuition. Is this statement true or false?

Complexity of Final Solution

One Pager Cheat Sheet

This is our final solution.

Great job getting through this. Let's move on.

Programming Categories

Popular Lessons