Good morning! Here's our prompt for today.

Implement a function that returns the Fibonnaci number for a given integer input. In a Fibonacci sequence, each number is the sum of the two preceding ones.

The simplest is the series: 1, 1, 2, 3, 5, 8, etc.

This is because:

1fibonacci(0) = 0
2fibonacci(1) = 1
3fibonacci(2) = 1
4fibonacci(3) = 1 + 1 = 2
5fibonacci(4) = 1 + 2 = 3
6fibonacci(5) = 2 + 3 = 5

So if we were to invoke fibonacci(5), we'd want to return 5 (because the second to last number was 2 + last number was 3).

Constraints

• The value of n will always be a non negative integer and <=40
• The answer is guaranteed to fit in the integer data type
• Expected time and space complexity are both O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  console.log('PASSED: ' + '`fibonacci(34)` should return `5702887`');

var assert = require('assert');

​

/*

 * @param {number} n The Fibonacci number to get.

 * @returns {number} The nth Fibonacci number

 */

​

function fibonacci(num) {

  // fill this in

  return num;

}

​

try {

  assert.equal(fibonacci(1), 1);

​

  console.log('PASSED: ' + '`fibonacci(1)` should return `1`');

} catch (err) {

  console.log(err);

}

​

try {

  assert.equal(fibonacci(17), 1597);

​

  console.log('PASSED: ' + '`fibonacci(17)` should return `1597`');

} catch (err) {

  console.log(err);

}

​

try {

Here's our guided, illustrated walk-through.

How do I use this guide?

Recall the definition of the Fibonacci numbers: they are a sequence of integers in which every number after the first two (0 and 1) is the sum of the two preceding numbers. To arrive at the sequence, we can quickly recognize there's a pattern in place, where we are repeating a similar calculation multiple times with different numbers.

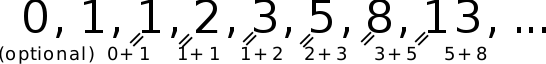
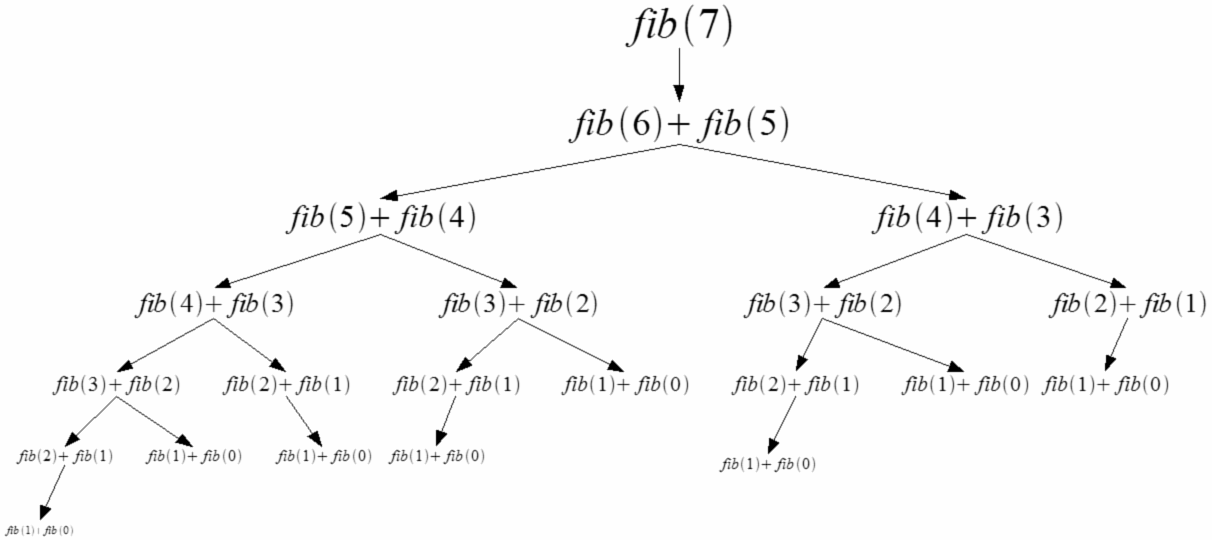
Time to reach into our toolbox-- this can readily be solved with recursion. At each recursive call, run the same calculation based off the same function for the prior elements. You can see the pseudo-code provided for how this can be accomplished.

xxxxxxxxxx

Routine: f(n)

Output: Fibonacci number at the nth place

​

Base case:

1. if n==0 return 0

2. if n==1 return 1

​

Recursive case:

1. temp1 = f(n-1)

2. temp2 = f(n-2)

3. return temp1+temp2

So we know we simply recursively call a method that returns the sum of the previous two fibonacci numbers.

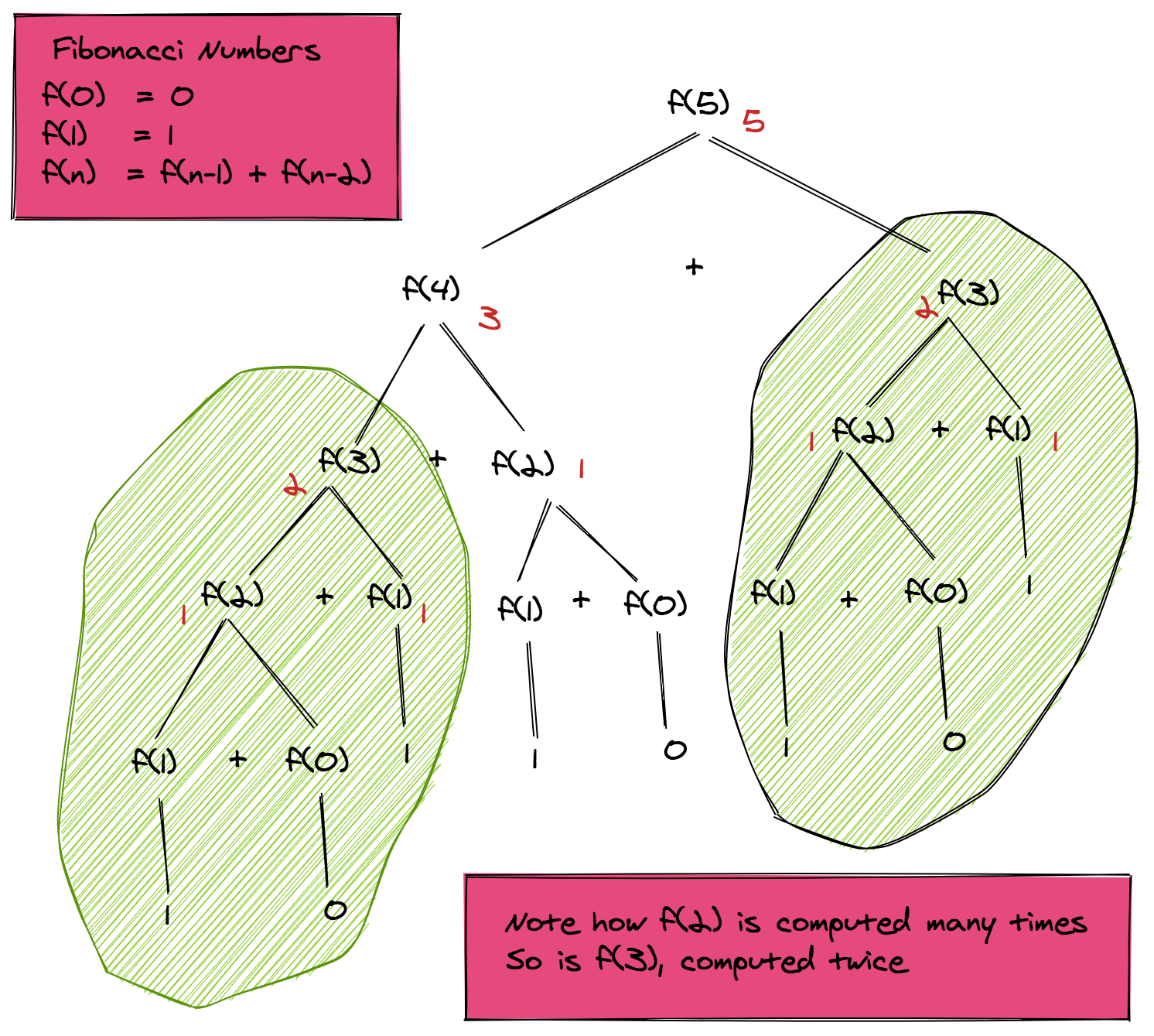
If we look closely at the recursive tree, we can see that the function is computed twice for f(3), thrice for f(2) and many times for the base cases f(1) and f(0). The overall complexity of this pseudo-code is therefore exponential O($2^n$). We can very well see how we can achieve massive speedups by storing the intermediate results and using them when needed.

xxxxxxxxxx

Routine: fibonacciFast

Input: n

Output: Fibonacci number at the nth place

Intermediate storage: n1, n2 to store f(n-1) and f(n-2) respectively

​

1. if (n==0) return 0

2. if (n==1) return 1

3. n1 = 1

4. n2 = 0

5. for 2 .. n

    a. result = n1+n2           // gives f(n)

    b.   n2 = n1                // set up f(n-2) for next number

    c.   n1 = result            // set up f(n-1) for next number

6. return result

To memo-ize previous function calls, we can use a nifty memoize function.

What we're doing in memoize is utilizing a hash map (in this case, a plain old JS object) to store previous calculations. The key will be the arguments called-- for example, 5 in fib(5), and the value attached will be the result of the callback. In this example, we utilize the closure pattern so that ...args are the parameters of the callback function, and not of memoize.

xxxxxxxxxx

const memoize = (callback) => {

  let memo = {};

  return (...args) => {

    if (memo[args]) {

      return memo[args];

    } else {

      memo[args] = callback(args);

      return memo[args];

    }

  };

};

Now we can wrap our fibonacci function with the memoize function for a more efficient solution. During an interview, it's best to bring up the use of this pattern whenever there's several repeating subproblems.

xxxxxxxxxx

const memoize = (callback) => {

  let memo = {};

  return (...args) => {

    if (memo[args]) {

      return memo[args];

    } else {

      memo[args] = callback(args);

      return memo[args];

    }

  };

};

​

function fibonacci(num) {

  if (num < 0) throw "num must be >= 0";

  if (num === 0) return 0;

  if (num === 1) return 1;

​

  return fibonacci(num - 1) + fibonacci(num - 2);

}

​

const memoizedFib = memoize(fibonacci);

const result = memoizedFib(30);

console.log(result);