So we know we simply recursively call a method that returns the sum of the previous two fibonacci numbers.

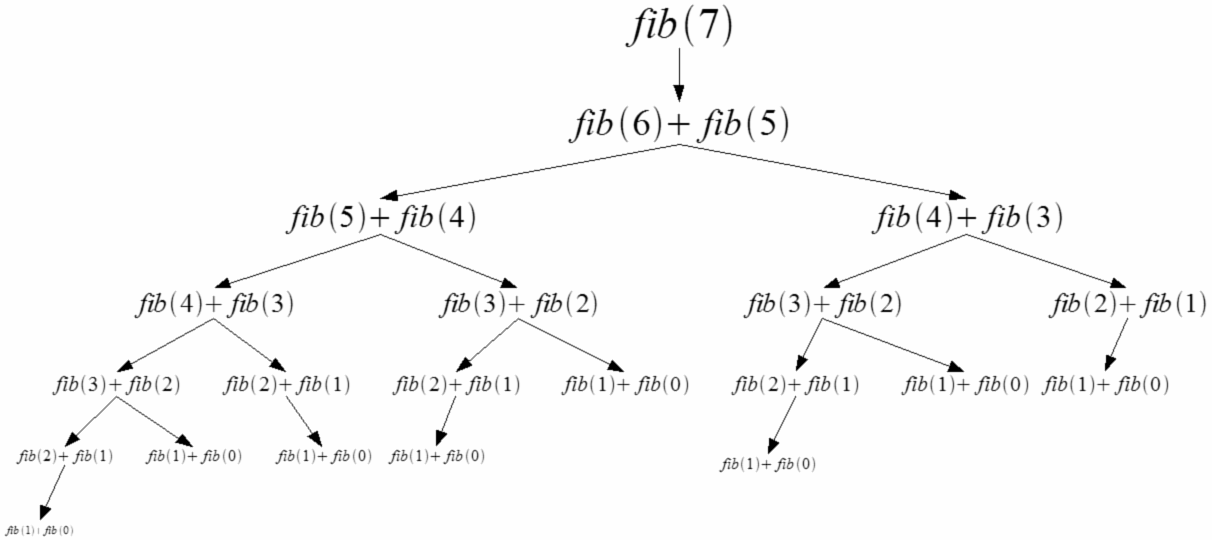
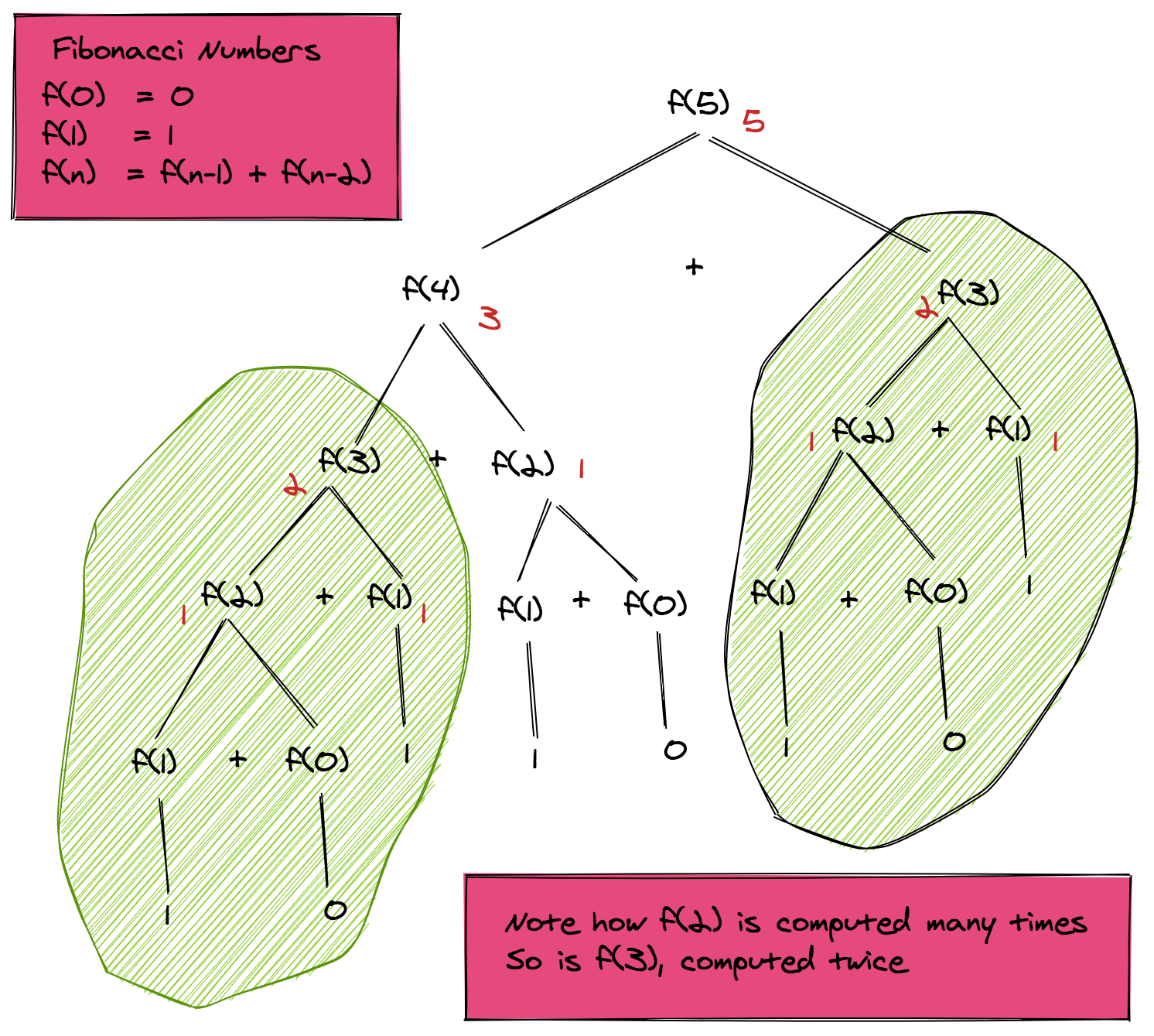
If we look closely at the recursive tree, we can see that the function is computed twice for f(3), thrice for f(2) and many times for the base cases f(1) and f(0). The overall complexity of this pseudo-code is therefore exponential O($2^n$). We can very well see how we can achieve massive speedups by storing the intermediate results and using them when needed.

xxxxxxxxxx

Routine: fibonacciFast

Input: n

Output: Fibonacci number at the nth place

Intermediate storage: n1, n2 to store f(n-1) and f(n-2) respectively

​

1. if (n==0) return 0

2. if (n==1) return 1

3. n1 = 1

4. n2 = 0

5. for 2 .. n

    a. result = n1+n2           // gives f(n)

    b.   n2 = n1                // set up f(n-2) for next number

    c.   n1 = result            // set up f(n-1) for next number

6. return result