AlgoDaily - Validate a BST

Good morning! Here's our prompt for today.

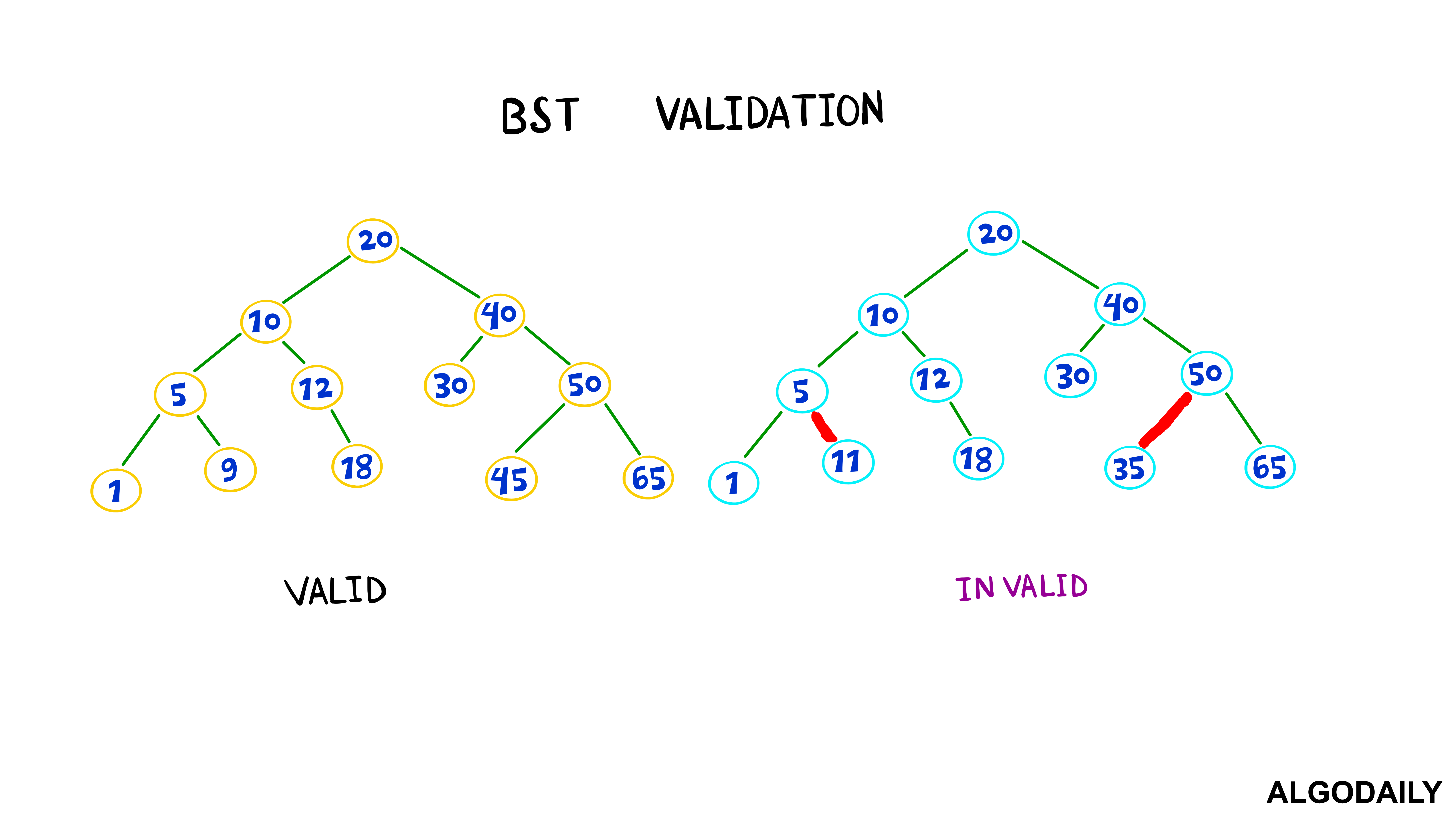
Given a binary search tree like the one below, can you write a function that will return true if it is valid?

SNIPPET

Recall that a BST is valid only given the following conditions:

The left child subtree of a node contains only nodes with values less than the parent node's.
The right child subtree of a node contains only nodes with values greater than the parent node's.
Both the left and right subtrees must also be BSTs.

You can assume that all nodes, including the root, fall under this node definition:

JAVASCRIPT

1class Node {
2	constructor(val) {
3		this.value = val;
4		this.left = null;
5		this.right = null;
6	}
7}

The method may be called like the following:

JAVASCRIPT

1root = new Node(5);
2root.left = new Node(3);
3root.right = new Node(9);
4
5console.log(isValidBST(root));

Constraints

Length of the given tree <= 100000
The nodes in the tree will always contain integer values between -1000000000 and 1000000000
Expected time complexity : O(n)
Expected space complexity : O(logn) or O(d) where d is the depth of the tree

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
  console.log('PASSED: ' + '`isValidBST(tree1)` should return `false`');
 
var assert = require('assert');
​
function isValidBST(self, root) {
  // Fill in this method
  return self;
}
​
function inOrder(root, output) {}
​
function Node(val) {
  this.val = val;
  this.left = null;
  this.right = null;
}
​
// Regular binary trees
var tree1 = new Node(4);
tree1.left = new Node(1);
tree1.right = new Node(3);
​
var tree2 = new Node(5);
tree2.left = new Node(10);
tree2.left.left = new Node(17);
tree2.left.right = new Node(3);
tree2.right = new Node(8);
​
// Binary search trees
var tree3 = new Node(6);
tree3.left = new Node(3);

Here's how we would solve this problem...

How do I use this guide?

Let's test your knowledge. Click the correct answer from the options.

Which of the following is NOT a property of the Binary Search Tree data structure?

Click the option that best answers the question.

The LEFT subtree of a node contains only nodes with keys LESS than the node's key.
The LEFT subtree of a node contains only nodes with keys GREATER than the node's key.
The RIGHT subtree of a node contains only nodes with keys GREATER than the node's key.
Both the LEFT and RIGHT subtrees must also be binary search trees.

Build your intuition. Could you figure out the right sequence for this list?

Select the proper order of an in-order traversal for a Binary Search Tree:

Press the below buttons in the order in which they should occur. Click on them again to un-select.

Options:

Visit the root.
Traverse the left subtree, i.e., call Inorder(left-subtree)
Traverse the right subtree, i.e., call Inorder(right-subtree)

Are you sure you're getting this? Click the correct answer from the options.

A BST has integers as node keys. For an in-order traversal of a BST, in what order do the node keys get processed?

Click the option that best answers the question.

Ascending
Descending
Random
Zig-Zag

Build your intuition. Click the correct answer from the options.

What would be the result of the following recursive function?

PYTHON

1def func(num):
2    if n == 4:
3       return n
4    else:
5       return 2 * func(n+1);
6
7func(2)

Click the option that best answers the question.

4
3
16
infinity

Try this exercise. Fill in the missing part by typing it in.

The following is working code validating a Binary Search Tree in Python.

SNIPPET

1class Solution:
2  def is_valid_bst(self, root):
3    output = []
4    self.in_order(root, output)
5    
6    for i in range(1, len(output)):
7      if output[i-1] >= output[i]:
8        return False
9
10    return True
11
12  def in_order(self, root, output):
13    if root is None:
14      return
15    ____________________________________
16    output.append(root.val)
17    self.in_order(root.right, output)

Write the missing line below.

Inputs and outputs

Let's start, as always, with a few examples. Running through some inputs helps our brains to intuit some patterns. This may help trigger an insight for a solution.

Let's say we just have this simple binary search tree:

xxxxxxxxxx
 
/*
​
  5 
 / \ 
3   9 
​
*/

Is this valid? It sure seems so, the first criteria that comes to mind being that 3 is less than 5, and therefore that node is to the left. On the other hand, 9 is greater than 5, and thus is to the right. Alright, this seems like a no brainer, let's just check that every left child is smaller than the root, and every right child is greater than the local root.

Brute force solution?

Here's a possible early solution:

xxxxxxxxxx
 
function isValidBST(root) {
  if (root.left < root.val && root.right > root.val) {
    return true;
  }
}

We should be able to run through that method recursively, and check every subtree. Is that enough though? Let's extend our tree a bit and add two more children to the root's left child.

xxxxxxxxxx
 
/*
​
    5 
   / \ 
  3   9 
 / \
2   8
​
*/

Is the above a valid binary search tree? It is not -- if our root is 5, the entire left subtree (with 3 as the root) needs to have keys less than the parent tree's root key. Notice that the 8 is still to the left of 5, which is invalidates the simple recursive function from above.

Pattern recognition

In thinking about what we need to do with this tree, there clearly needs to be some form of traversal so that we can check the nodes against each other.

Two questions we can ask are: 1. Is there a way to compare node values without, or possibly exclusive, of the traversal? 2. What technique or pattern can help us easily compare tree values?

The answer is an in-order depth-first search of the tree. As you'll recall, an in-order DFS follows the standard depth-first method of going as deep as possible on each child before going to a sibling node. However, the difference is, it will process all left subtree nodes first, do something with the root or current node, and then process all right subtree nodes.

Because of the definition of a binary search tree, valid ones will produce an in-order DFS traversal in sorted order from least to greatest.

Thus, we can use this to our advantage. Here's a simple inOrder method to run through a binary search tree and return a list of node values.

xxxxxxxxxx
 
function inOrder(root, output) {
  if (!root) {
    return;
  }
​
  inOrder(root.left, output);
  output.append(root.val);
  inOrder(root.right, output);
}

If this is in sorted order, we know that this is valid. We can check this iterating through the returned list, checking that each iterated element's value is greater than the previous iteration's. If we get to the end, we can return True. If the opposite is ever true, we'll immediately return False.

Complexity of Final Solution

Let n be the size of the tree. We traverse through all n tree nodes using recursion for O(n) time complexity, and we have O(logn) space complexity due to recursion or O(d) where d is the depth of the tree.

One Pager Cheat Sheet

Write a function, isValidBST(node), that returns true if the given binary search tree is valid according to the defined conditions.
The left subtree of a node in a Binary Search Tree (BST) must only contain nodes with keys LESS than the node's key, while the right subtree must contain nodes with keys GREATER than the node's key to maintain its in-order traversal which produces an increasing order of nodes.
The In-order traversal of a Binary Search Tree follows a specific algorithm to access data in a very efficient manner, visiting each node left to right by recursively calling the Inorder() function.
An in-order traversal of a BST processes the node keys in ascending order by beginning at the smallest key and progressively traversing rightward.
The given recursive function will return 2 times the result of the recursive call until the if statement evaluates to True, in which case the value of n is returned, which in the example is 4 and the result of func(2) is 16.
Running through inputs with a binary search tree can help trigger insights for a solution.
Checking if every left child is smaller than the root, and every right child is greater than the local root is a brute force solution for determining the direction of nodes in a tree.
We can recursively check every subtree by running through the method, but to ensure accuracy we should extend the tree by adding two more children to the root's left child.
We can use an in-order depth-first search to check a binary search tree for validity by comparing its processed node values in sorted order.
We can determine if a given tree is valid in O(n) time complexity and O(logn) space complexity by iterating through all n elements and checking that each successive element is greater than the previous iteration.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function isValidBST(root) {
  const searchResults = [];
  inOrder(root, searchResults);
​
  for (let i = 1; i < searchResults.length; i++) {
    if (searchResults[i - 1] >= searchResults[i]) {
      return false;
    }
  }
​
  return true;
}
​
function inOrder(root, output) {
  if (!root) {
    return;
  }
​
  inOrder(root.left, output);
  output.push(root.val);
  inOrder(root.right, output);
}
​
function Node(val) {
  this.val = val;
  this.left = null;
  this.right = null;
}
​
// Regular binary trees

That's all we've got! Let's move on to the next tutorial.

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Here's how we would solve this problem...

Let's test your knowledge. Click the correct answer from the options.

Click the option that best answers the question.

Build your intuition. Could you figure out the right sequence for this list?

Options:

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Try this exercise. Fill in the missing part by typing it in.

Inputs and outputs

Brute force solution?

Pattern recognition

Complexity of Final Solution

One Pager Cheat Sheet

This is our final solution.

That's all we've got! Let's move on to the next tutorial.

Programming Categories

Popular Lessons