Good morning! Here's our prompt for today.

This problem is a fun combination of the famous Two Sum problem combined with a binary search tree. Given the root of a binary search tree, and a target integer K, return true if there exist two nodes in the said tree whose sum equals K. If no pair fits this match, return false.

Say we are given this tree:

1/***
2
3  Input:
4    5    
5   / \     
6  3   8
7 /        
81
9
10***/

Each node is defined in the following manner:

1class Node {
2	constructor(val) {
3		this.value = val;
4		this.left = null;
5		this.right = null;
6	}
7}

And thus the below setup and execution code should hold true:

1const root = new Node(5);
2root.left = new Node(3);
3root.right = new Node(8);
4root.left.left = new Node(1);
5
6const target = 11;
7
8twoSumFromBST(root, target);
9// true because 3 + 8 = 11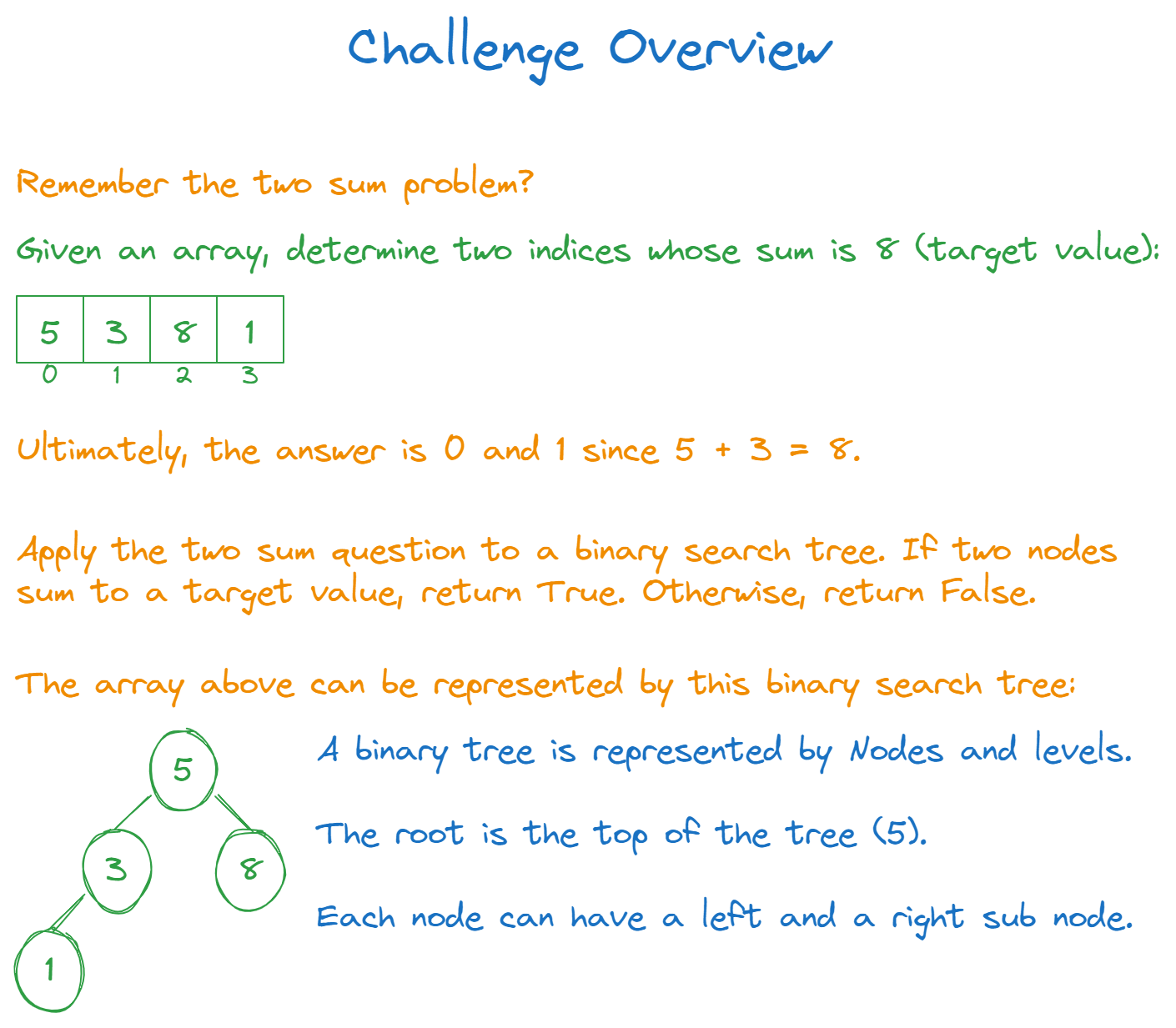

Constraints

• Number of vertices in the tree <= 100000
• The values in the vertices will be between -100000 and 1000000
• The target value will be between -100000 and 100000
• Expected time complexity : O(n)
• Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

    'PASSED: var testRoot = new Node(5);testRoot.left = new Node(3);testRoot.right = new Node(8);testRoot.left.left = new Node(1);var target = 11;assert.equal(twoSumFromBST(testRoot, target), true);'

var assert = require('assert');

​

function inOrder(root) {}

​

function twoSumFromBST(root, target) {

  // Fill in this method

  return root;

}

​

class Node {

  constructor(val) {

    this.value = val;

    this.left = null;

    this.right = null;

  }

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

Here's how we would solve this problem...

How do I use this guide?