AlgoDaily - Fundamental Sorting Algorithms: Bubble and Insertion

Home > Data Structures and Algorithms 🚀 > Pointers and Windows > Fundamental Sorting Algorithms: Bubble and Insertion

This tutorial is about two fundamental, and basic, sorting algorithms. If you are new to sorting, I'd recommend you come up with your own algorithm for sorting arrays first, and then compare it with these algorithms. These fundamental sorting techniques give you important insights into:

How to sort arrays
How you can improve an algorithm, and
Under what conditions you should apply a certain sort procedure

xxxxxxxxxx
printArray(myArr2);
 
function swap(X, ind1, ind2) {
    let temp = X[ind1];
    X[ind1] = X[ind2];
    X[ind2] = temp;
}
​
function bubbleSort(X) {
    let n = X.length;
    let sorted = false;
    let totalSorted = 0;
    while (totalSorted < (n-1) && !sorted) {
        sorted = true;
        for(let i = 1; i <= n-1-totalSorted; ++i) {
            if (X[i-1] > X[i]) {
                swap(X, i-1, i);
                sorted = false;
            }
        }
        totalSorted++;
    }
}
​
function insertionSort(X) {
    let totalSorted = 1;
    let n = X.length;
    while (totalSorted <= (n-1)) {
        let i = totalSorted;
        while(i > 0 && X[i-1] > X[i]) {
            swap(X, i-1, i);

Bubble Sort

Bubble sort is one of the simplest sorting methods. In case you are wondering where this odd name for a sorting technique came from-- lighter bubbles in water always float to the top. Heavy objects sink to the bottom.

We use a similar idea when sorting items in an array: "bubble down" heavier or bigger keys. Alternatively, we can bubble up lighter keys.

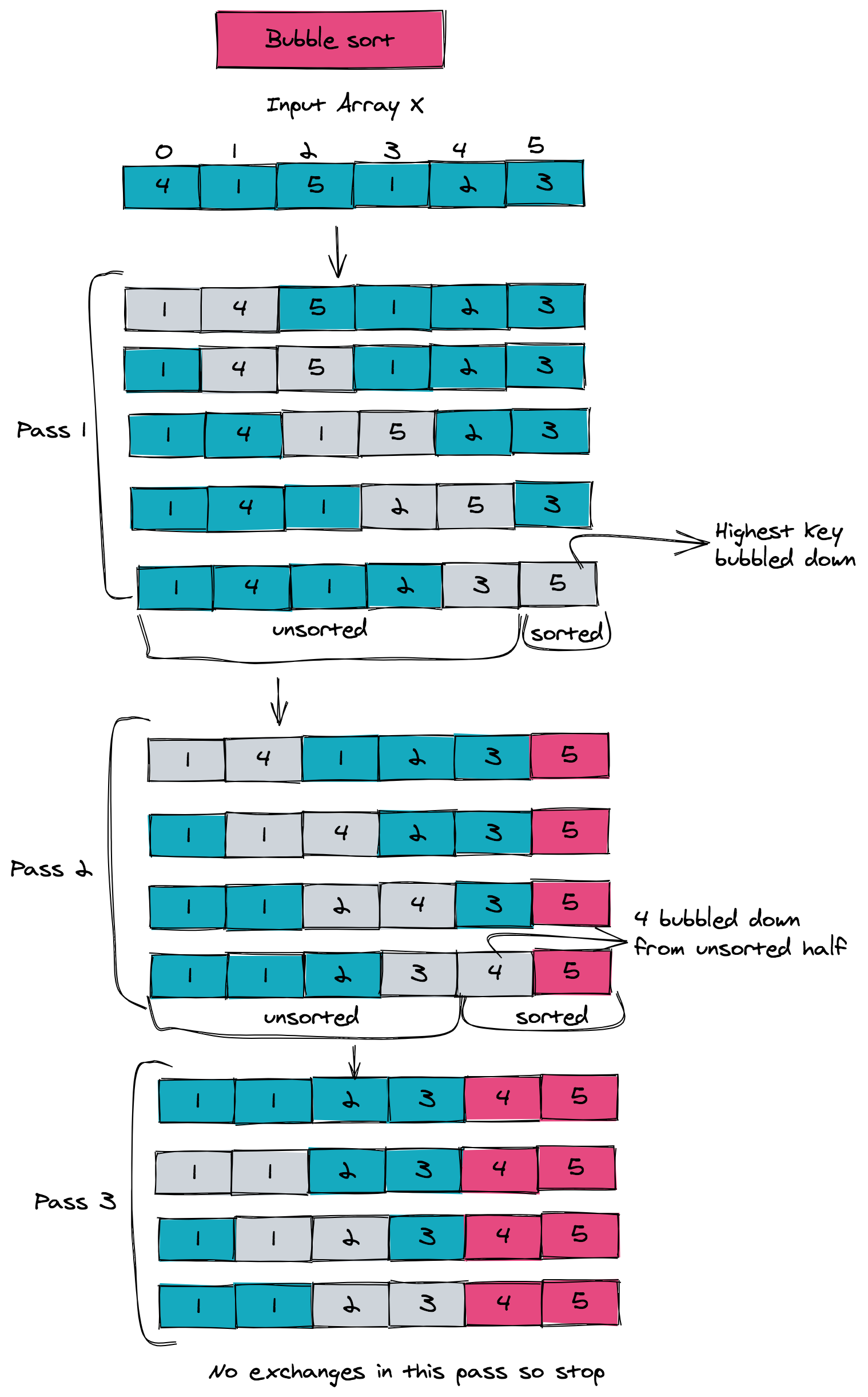
Let's take a look at this technique that bubbles down all the heavier keys to the end of the array. Bubble sort divides the entire array into a sorted half and an unsorted half. It works by using the following principle:

Maintain an unsorted left sub-array and a sorted right sub-array.
Bubble down the heaviest item in the unsorted half to the right sub-array.

How do you bubble down the heaviest key? One way of doing it is by comparing consecutive keys and swapping if left key is greater than the right key. Here is the complete pseudo-code:

SNIPPET

1Routine: bubbleSort
2Input: Unsorted array X of size n
3
41. sorted = false
52. totalSorted = 0
63. while (totalSorted < (n-1) and !sorted)
7    {
8        a.sorted = true     // will remain true if no swaps are made
9        b. for i=1 .. (n-1 - totalSorted)
10        {
11            i. if X[i-1] > X[i]
12                {     swap(X[i-1],X[i])
13                      sorted = false
14                }
15        }
16        c. totalSorted++
17    }

xxxxxxxxxx
 
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        // Swap here
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
​
  console.log(arr);
}
​
bubbleSort([3, 2, 1]);

Build your intuition. Click the correct answer from the options.

Which is correct when looking at bubble sort's time complexity?

Click the option that best answers the question.

O(n^2) in worst case
O(n log n) in worst case
O(n) in worst case

Notice how beautifully the pseudo-code sorts the array. The outer loop of the algorithm represents a pass of the algorithm. The inner for loop compares consecutive items and swaps them if needed.

The boolean flag sorted is set to true before the inner for-loop for comparing successive items. If no swap is made, it remains true and we can break out of the outer loop.

This makes bubble sort a very special algorithm, as it is one of the few sorting algorithms that tells you when an array is sorted. You can stop running further passes if the array is sorted. The entire process is illustrated in the figure below. Notice how the sorted and unsorted parts of the array is maintained, and how the algorithm stops once the array is sorted.

Complexity of Bubble Sort

The time complexity of bubble sort depends upon the input array. As we saw in our pseudo-code, if our array is already sorted, it will make only one pass through the input array. Hence, for a sorted array, its time complexity is O(n). However, in the worst-case scenario, it will make roughly O(n) passes through the array, where each pass is approximately O(n) time. This makes the overall time complexity quadratic, i.e., O(n $^{2}$ ) in the worst case.

The sorting is in place sorting and does not use any extra array memory. Thus the space complexity is O(1).

Insertion Sort

Insertion sort is another marvelous sorting algorithm, one that's pretty simple to understand and easy to implement.

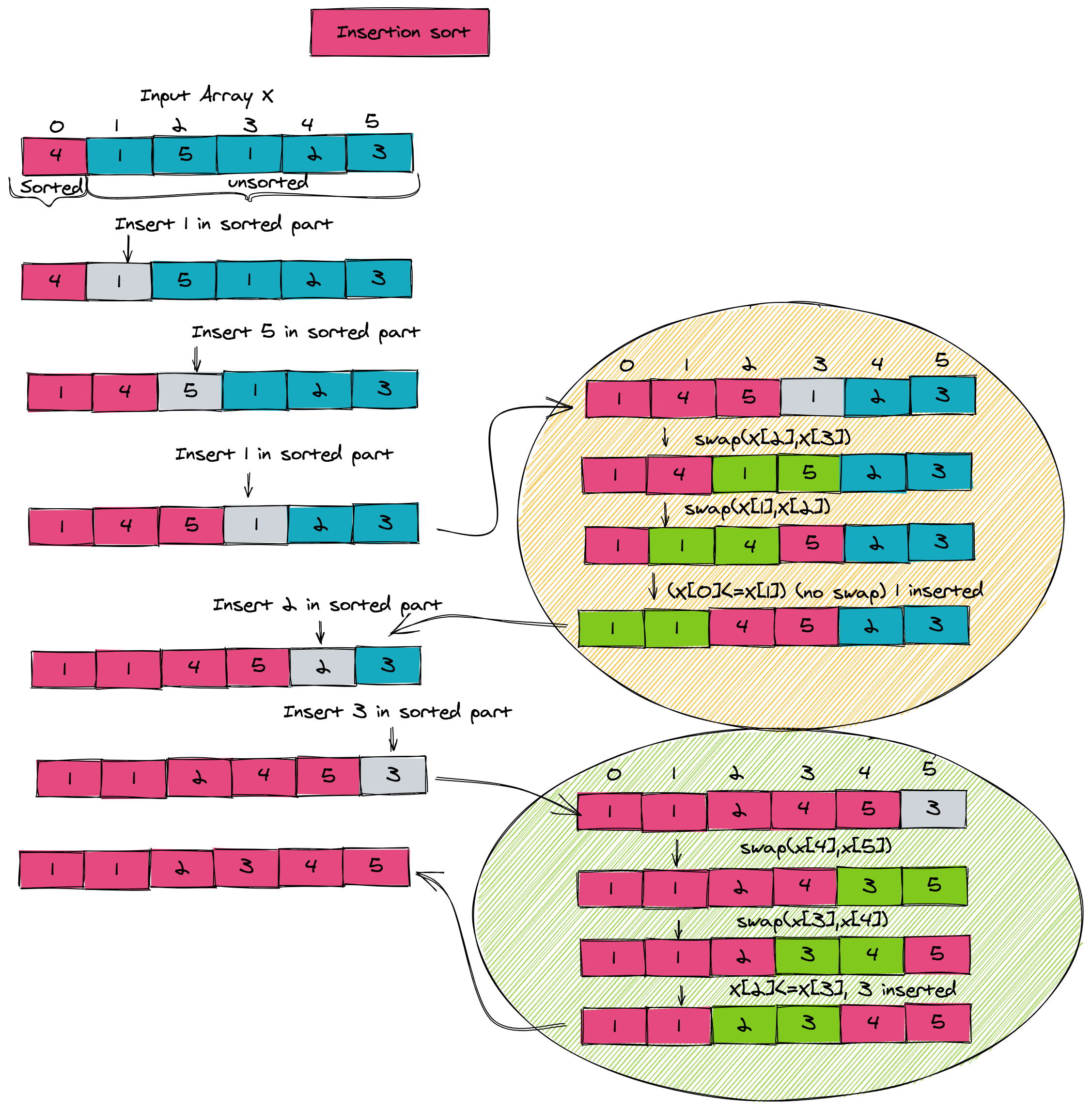
The idea is similar to bubble sort. Think of your input array as being made of a sorted left half and an unsorted right half.

One by one, insert an item in its correct place in the sorted half. Insertion is done by comparing the item with successive items before it, and swapping them if needed. To reiterate the steps:

Maintain a sorted left sub-array and an unsorted right sub-array.
Insert the first key from the unsorted part into its correct place in the sorted half.

The entire pseudo-code that accomplishes the sort is provided here:

SNIPPET

1Routine: insertionSort
2Input: Unsorted array X of size n
3
41. totalSorted = 1
52. while totalSorted <= (n-1)
6    {
7        // insert the item at index position totalSorted into top half
8        // by successive comparison with items before it
9        b. i = totalSorted
10        c. while(i > 0 and X[i-1]>X[i])
11        {
12            i. swap(X[i-1], X[i])
13            ii. i--
14        }
15        totalSorted++
16    }

xxxxxxxxxx
 
function insertionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    const val = arr[i];
​
    // Arrange the elements prior to the current
    // but greater than it to one position ahead
    let j = i - 1;
    while (j >= 0 && val < arr[j]) {
      arr[j + 1] = arr[j];
      j -= 1;
    }
    arr[j + 1] = val;
  }
  return arr;
}
​
const arr = [41, 19, 23, 3, 4, 19];
console.log(insertionSort(arr));

Are you sure you're getting this? Click the correct answer from the options.

Which is correct when looking at insertion sort's time complexity?

Click the option that best answers the question.

O(n$^2$) in worst case
O(n log n) in worst case
O(n) in worst case

Again, what a marvelous piece of code! It's sorting an entire array in a simple manner. The outer loop represents a pass of the algorithm and the inner loop inserts one item from the unsorted part into the sorted part by successive comparisons. The whole process is illustrated in the figure below. Notice how the big bubbles illustrate the insertion process of the inner loop.

Complexity of Insertion Sort

Insertion sort, like bubble sort, has a time complexity that depends upon the input array.

We can see that if we input a sorted array, then insertion sort makes only one pass through the array, and thus its time complexity is O(n). However, in the worst-case scenario (say the input array is in descending order) then there are O(n) items to be inserted. Each insertion would make roughly O(n) comparisons, giving an overall quadratic time complexity-- O(n $^{2}$ ).

The sorting is in place and does not require any extra array memory making its space complexity O(1).

Wrapping up

In summary, insertion sort and bubble sort are great sorting algorithms. You can use them if you have a very small array and want a quick implementation. Here's a really important point:

If you know in advance that your array is almost sorted, then both bubble sort and insertion sort would be very efficient.

However, if you know nothing about your array (or you have a large array), then go for a more efficient algorithm.

I hope you enjoyed this tutorial on basic sorting algorithms. Good luck sorting!

Let's test your knowledge. Click the correct answer from the options.

Which is correct when looking at bubble sort's space complexity?

Click the option that best answers the question.

O(n^2) in worst case
O(n) in worst case
O(1) in worst case

Are you sure you're getting this? Click the correct answer from the options.

Which is correct when looking at insertion sort's space complexity?

Click the option that best answers the question.

O(n$^2$) in worst case
O(n) in worst case
O(1) in worst case

One Pager Cheat Sheet

If you are new to sorting, come up with your own algorithm first and then compare it to the fundamental sorting techniques to gain important insights into how to sort arrays, improve an algorithm and when to apply a certain sort procedure.
Bubble sort starts by dividing the array into a sorted and unsorted sub-array, and compares consecutive items to sort them by "bubbling down" heavier items and "bubbling up" lighter items.
Bubble Sort has a time complexity of O(n^2), as it must compare all consecutive pairs and perform a swap operation for each comparison, with a total of n * (n-1) / 2 comparisons necessary.
Bubble sort is a very special algorithm which is one of the few sorting algorithms that tells you when an array is sorted and can stop running further passes if the array is already sorted, thus having an O(n) best-case complexity and an O(n $^{2}$ ) worst-case complexity with an O(1) space complexity.
Insertion Sort is an easy-to-implement algorithm that swaps items if needed in order to insert them in their correct place in the sorted sub-array.
Insertion Sort has a worst-case time complexity of O(n$^2$), due to needing to iterate through the sorted sub-array and compare each element to each item before it in an O(n) operation.
Insertion sort is an in place sorting algorithm which has time complexity of O(n) if the input is already sorted, and worst case time complexity of O(n$^2$) if the input is in descending order.
If you know in advance that your array is almost sorted, then **both bubble sort and insertion sort would be very efficient**.
Bubble sort is an in-place sorting algorithm with O(1) space complexity, making it an efficient method for sorting data.
Insertion Sort has excellent `space complexity of O(1), requiring only constant extra space**.

Bubble Sort

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Complexity of Bubble Sort

Insertion Sort

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Complexity of Insertion Sort

Wrapping up

Let's test your knowledge. Click the correct answer from the options.

Click the option that best answers the question.

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

One Pager Cheat Sheet

Programming Categories

Popular Lessons