The Theory

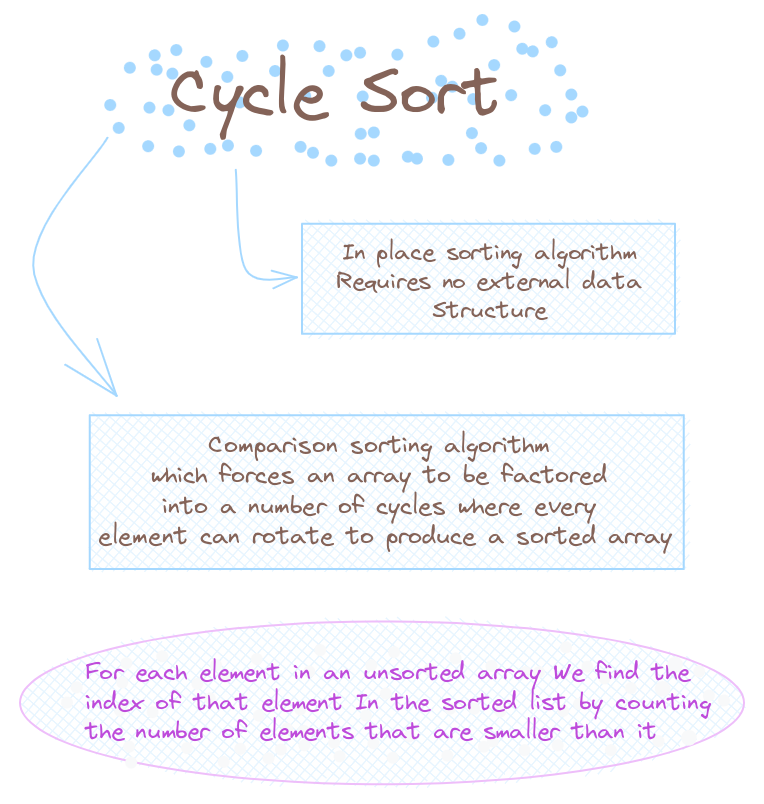
The cycle sort algorithm is an in-place sorting algorithm. This means that no external data structure (such as a list or heap) is required to perform the cycle sort operation.

The underlying assumption for the cycle sort algorithm is that an unsorted list is similar to a graph, where nodes are connected with edges. We can assume that a relationship between nodes A and B exists if-- in order to sort the array-- the element present at node A should be at the index of node B when rotated.

This is the big idea: Given an element a, we can find the index at which it will occur in the sorted list by simply counting the number of elements in the entire list that are smaller than a.

Of course, it's always hard to understand a new technique at first in abstract, so let's see cycle sort in action with the help of an example.

Suppose we have the following list or array of elements:

1[9, 4, 6, 8, 14, 3]

Understanding Cycle Sort Through Visualization

Cycle sort is an in-place, non-comparing sorting algorithm. But what does that really mean? Imagine you're playing a game of musical chairs. Each number in the array is a player, and the index it needs to get to is its designated chair. This algorithm helps every player find their right chair without asking each player to compare themselves with others directly. Let's dive into the steps with enhanced clarity.

Step 1: The First Lap - Iterating Through the Array

Your first task is like a lap around the field to understand the players (numbers). You start at the first index and move forward one index at a time.

Step 2: Counting Ahead - Finding the Right Chair for Each Player

Once you're at an index, look ahead and see how many players (numbers) are smaller than the one you're standing next to. This is like finding out how many chairs are available ahead that suit our current player.

For example, you start with the number 9. There are 4 numbers smaller than 9 in the list (4, 6, 8, and 3). So 9 should actually be at the 4th index to be in its "right chair."

Step 3: Swap and Shuffle - Changing Places

Finally, you swap the current number with the number that belongs to the index you just found. It's like telling the player, "Hey, your chair is over there, go swap places!"

So in our example, 9 swaps places with 14 because 14 is currently sitting in the 4th chair, which is actually 9's chair.

Visualizing the Array Swap

Let's look at the array before and after the swap to drive the point home.

Before the Swap

Here's how our array looks initially:

1# Initial array
2idx:    0  1  2  3   4  5
3       [9, 4, 6, 8, 14, 3]
4        ^            ^  
5      (start)      (target)

The caret (^) symbols point to the elements we are focusing on: 9 at the start index, and 14 at the target index.

After the Swap

Once we've swapped the numbers, it looks like this:

1# After swapping
2idx:    0  1  2  3   4  5
3       [14, 4, 6, 8, 9, 3]
4        ^            ^  
5      (start)      (target)

Just like that, the player 9 has found its correct chair! The cycle sort algorithm will repeat this process for each number until everyone is in their right chair, and the array is sorted.

After the initial swapping, our array undergoes a transformation. Here's what happens:

The New Array Landscape

After the swap, our array looks like this:

1idx:       0  1  2  3   4  5
2updated = [14, 4, 6, 8, 9, 3]

The Visual Cue

You can think of the array like a series of parking spots. Initially, the car labeled '9' was in the first spot, and '14' was in the fifth spot. They've now switched places, and it's as if '14' moved to the front of the parking lot, while '9' took its place further back.

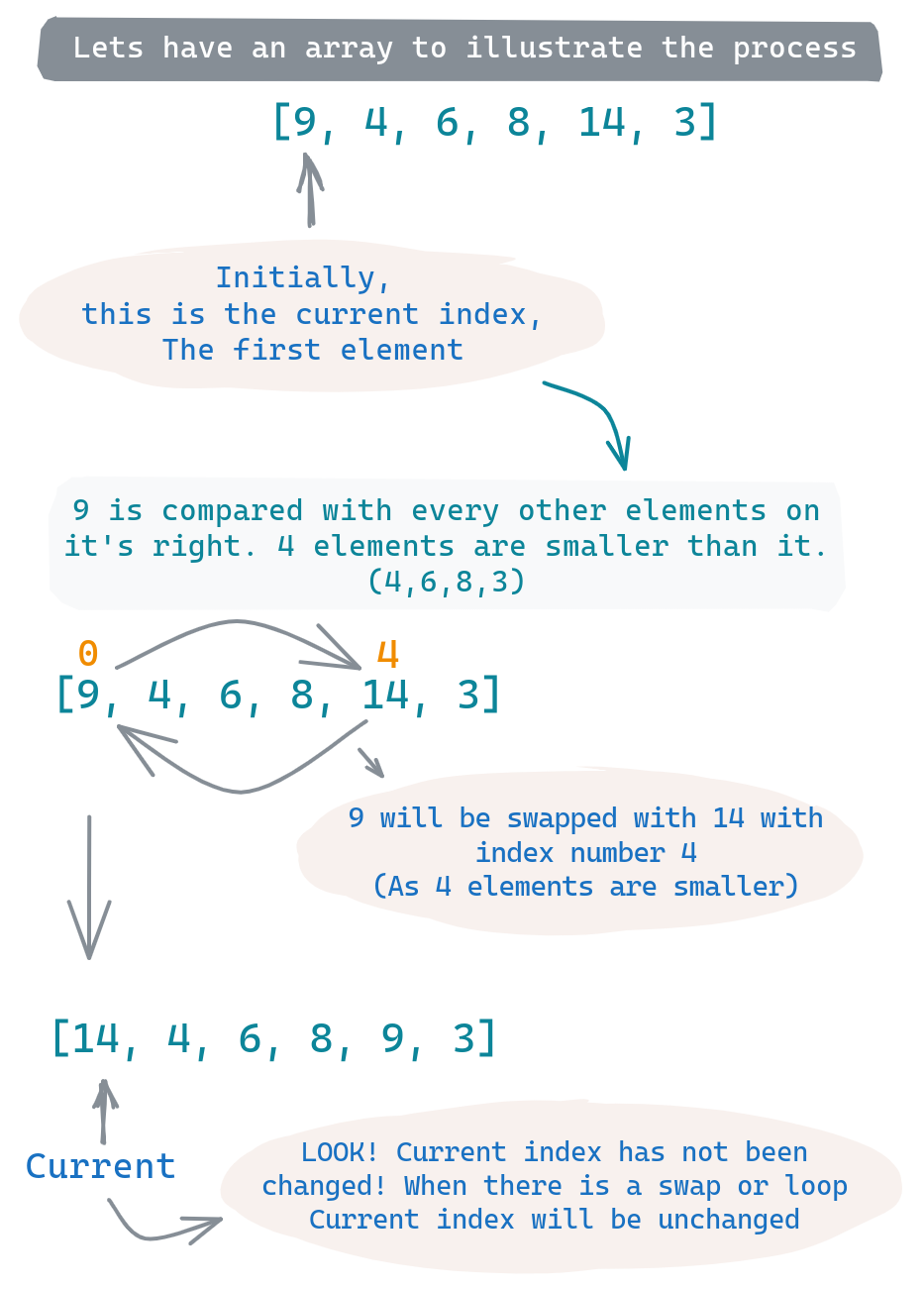
In the image above, the red arrows signify the movement of the numbers. The number '9' moved to the 4th index, and '14' took its original place at the 0th index.

Why This Matters?

This single swap is just the beginning. As we continue to iterate through each element in the array, these swaps will help every "player" (or car, if you like the parking lot analogy) find its "right chair" (or parking spot). Eventually, the entire array will be sorted, with each number in its designated position.

In essence, each swap is a step closer to organizing this chaotic parking lot into a well-arranged space where every car knows its spot.

Step 4: More Swaps and Musical Chairs

Looping Back: Focusing on the Same Index Again

Here comes an interesting twist. Normally, in sorting algorithms, once you're done with an index, you move to the next. But in cycle sort, you'll sometimes stay at the same index for another round. In our case, we haven't moved past index 0 yet; we're still dealing with what's now in that spot, which is 14.

Count, Swap, Repeat: The Sorting Continues

Let's take 14 and do the same counting exercise. How many elements are smaller than 14? Well, all of them! So, 14 should move to the last index, index 5.

Here's how the array transforms:

Before the Swap

The array before the swap:

1## previous
2idx:       0  1  2  3   4  5
3updated = [14, 4, 6, 8, 9, 3]
4           *

After the Swap

The array after the swap:

1## updated
2idx:       0  1  2  3   4  5
3updated = [3, 4, 6, 8, 9, 14]
4           ^               ^

Visually Mapping the Swap

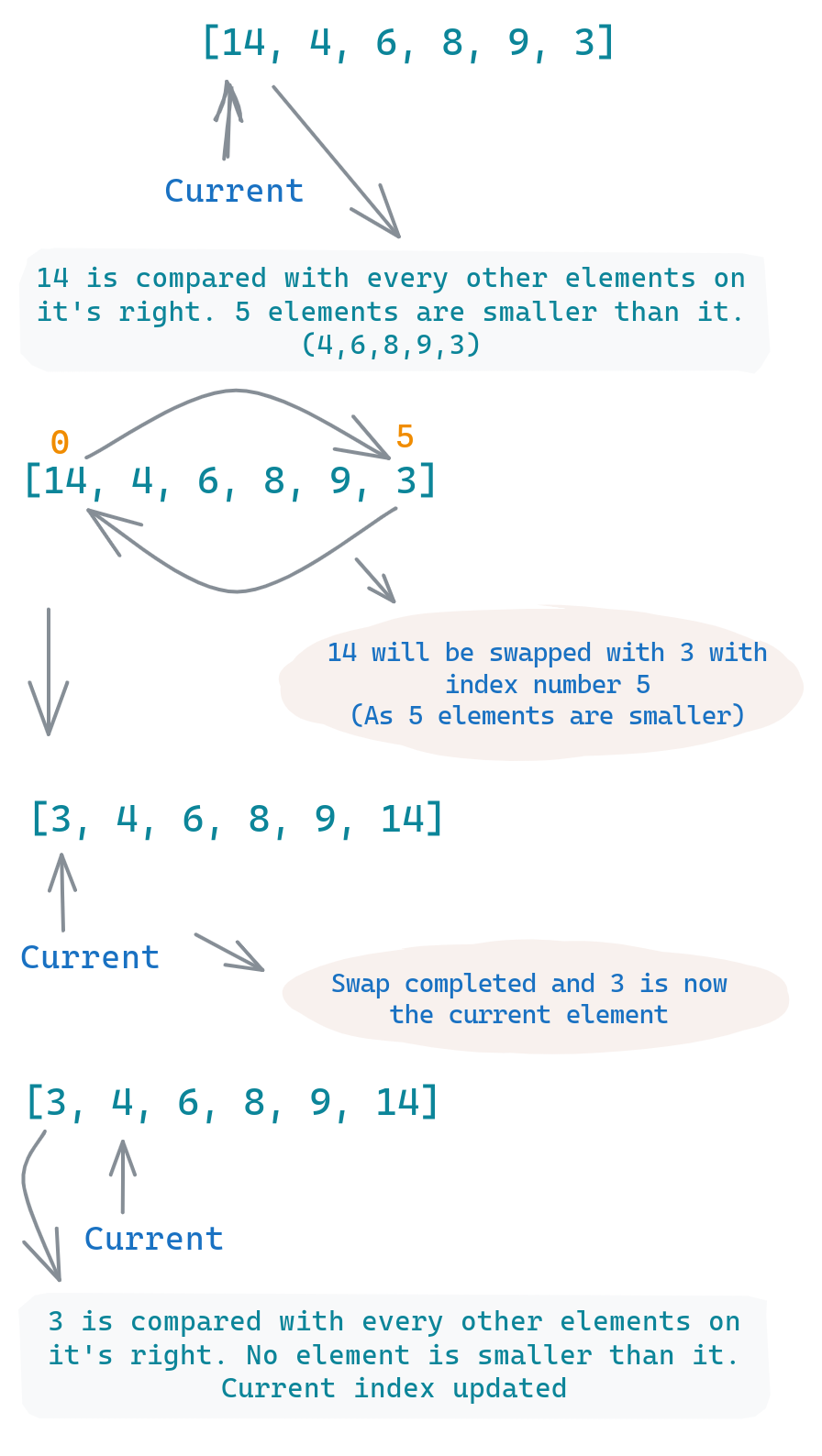
The red arrows in the image above signify the switch. '14' moves to its rightful place at the end of the array, and '3' comes to the front.

Why This Second Swap Matters

You might wonder, why did we not move to the next index? The reason is that the player (number) at the current index hasn't yet found its rightful chair (spot). Only when a player is in its designated chair do we move to the next one. Cycle sort is meticulous like that, ensuring everyone is where they should be, one step at a time. And this iterative refinement is what eventually sorts the entire array.

Step 5: Breaking the Cycle - When to Move On

The End of a Cycle

Up until this point, we've been diligently working through cycles at each index, making sure each player (number) finds its right chair (spot). But how do we know when to move on? The simple answer is: when a cycle is complete.

A cycle is complete when an element at the current index has either: 1. No more cycles left, meaning it's already in its designated chair. 2. No proceeding element greater than it, meaning it's the highest number and should be at the last index.

Once either of these conditions is met, it's time to move on to the next index.

Step 6: The Grand Continuation - Repeating for All Indexes

The Methodical March

We've sorted the chaos at the first index. Now, we repeat this process for the second index, the third index, and so on, until we reach the end of the array.

The Final Array Landscape

By the end of this exercise, each player will be sitting in their rightful chair, and our array will be beautifully sorted.

Visualizing the Remaining Process

The image gives us a neat summary of the journey we undertake. The arrows signify the flow of elements as they swap their places in search of their designated spots.

The Array Unveiled

After all the steps, cycles, and swaps, we finally have a sorted array. Let's take a moment to appreciate the beauty of an organized list:

1Sorted Array: [3, 4, 6, 8, 9, 14]

The Count of Operations

One of the perks of cycle sort is its efficiency. For our array, it took just a few operations to reach the sorted state:

1Operations: 3

Why This Matters

This count represents the number of elements that changed their positions in the sorting process. In our case, these elements were 9, 14, and 3.

Interestingly, the rest of the elements (4, 6, and 8) didn't have to move. They were already in their designated "chairs" or "parking spots," so to speak.

In the real world, less computational effort usually means faster execution times and less resource utilization, which is often a win-win in software engineering.

One Pager Cheat Sheet

• The Cycle Sort algorithm is an in-place sorting algorithm that takes advantage of the underlying assumption that an unsorted list is similar to a graph, where nodes are connected with edges, to find an index for an element in the sorted list by counting the number of elements smaller than it.`
• We can order an array by iterating through the elements, counting the number of smaller elements than the current element at each index, and swapping the current element with the element found at the index found in step 2.
• The updated array has been swapped, resulting in [14, 4, 6, 8, 9, 3].
• The element at index 0 was compared to all the remaining elements and its value was replaced by the value of the element at index 5 (3) to put it in its correct sorted position.
• The process of finding the correct element for each index of the array continues until no cycle or proceeding greater element is present.
• The total number of swap operations performed to find the correct element for the first index is 2.
• Cycle Sort is an in-place algorithm that finds and puts elements into their correct positions without requiring additional memory, taking maximum time for an unsorted array but being much faster for a sorted one.
• This algorithm can be implemented in Python.
• The sort_arr function accepts an input array and returns the number of write operations required to sort it in-place.
• Three operations were performed to sort the Array from [3, 4, 6, 8, 9, 14] to [3, 4, 6, 8, 9, 14].
• Cycle Sort is an in-place algorithm with fewer write operations, making it preferable in situations where write operations are expensive.
• Cycle sort is an in-place sorting algorithm that does not require any extra memory to complete the sorting process.