Selection Sort:

This algorithm is an in-place comparison-based algorithm that divided the list into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list. The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

The working of the selection sort algorithm is simulated in the below-mentioned figure:

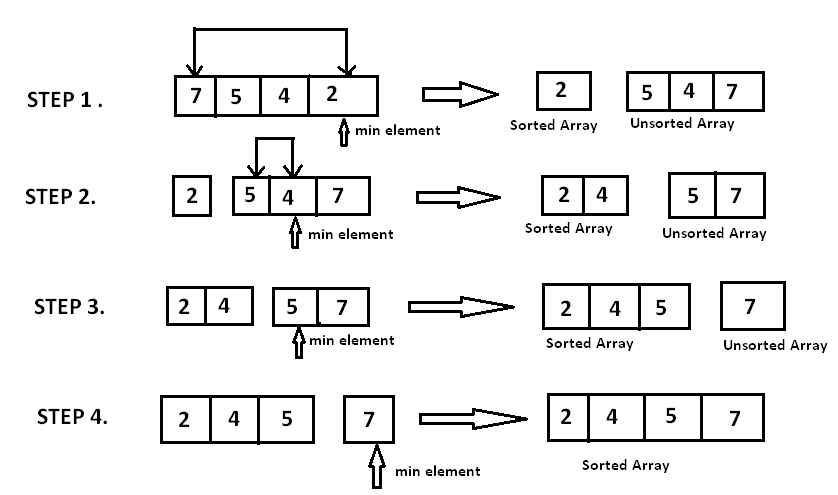
Here's some pseudo-code to follow:

1procedure selection sort
2   arr  : array of items
3   N    : size of list
4
5   for i = 1 to N - 1
6   /* set current element as minimum*/
7      min = i      
8      /* check the element to be minimum */
9      for j = i+1 to N
10         if arr[j] < arr[min] then
11            min = j;
12         end if
13      end for
14      /* swap the minimum element with the current element*/
15      if indexMin != i  then
16         swap arr[min] and arr[i]
17      end if
18   end for
19	
20end procedure

Time Complexity: O(N2)

Space Complexity: O(1)

Best Suited Scenario:

The selection sort algorithm is best suited with Array data structures and the given collection is in completely unsorted order. This algorithm is not feasible for a very large number of data set and this is likely due to its time complexity.

xxxxxxxxxx

const selectionSort = function(array) {

    let temp;

​

    for (let i = 0; i < array.length; i++){

        let minimum = i;

        for (let j = i + 1; j<array.length; j++) {

            if (array[j] < array[minimum])

                minimum = j;

        }

​

        temp = array[i];

        array[i] = array[minimum];

        array[minimum] = temp;

    }

​

    return array;

};

​

console.log(selectionSort([1, 3, 6, 7, 4, 8, 9, 1, 4, 6, 7]));

Insertion Sort:

This algorithm lies in the category of in-place comparison-based sorting algorithms. In this algorithm, a sub-collection is maintained which is always in order(sorted). For example, the lower part of an array is maintained to be ordered. An element that is to be added in this sorted collection has to find its correct place, and then it has to be inserted there. That’s why the algorithm is named ‘Insertion Sort’.

This sorting algorithm is basically a simple sorting algorithm that works similar to the way you sort the playing cards. The collection is virtually split into an ordered and an unordered part. Elements from the unordered portion are picked and placed at the correct index in the ordered part.

The working of the insertion sort algorithm is simulated in the below-mentioned figure:

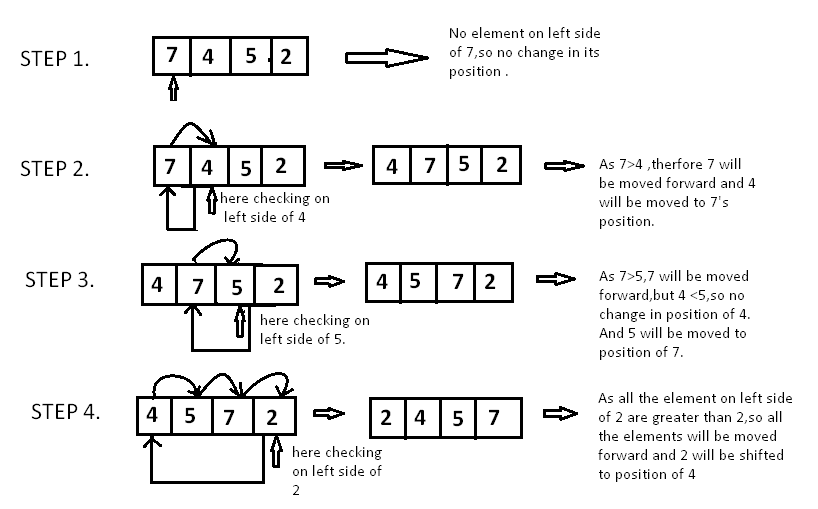
Here's the pseudocode:

1procedure insertionSort( A : collection of items )
2   int holePosition
3   int valueToInsert
4
5   for i = 1 to length(A) inclusive do:
6      /* select value to be inserted */
7      valueToInsert = A[i]
8      holePosition = i
9      /*locate hole position for the element to be inserted */
10      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
11         A[holePosition] = A[holePosition-1]
12         holePosition = holePosition -1
13      end while
14      /* insert the number at hole position */
15      A[holePosition] = valueToInsert
16   end for
17end procedure

Time Complexity: O(N2)

Space Complexity: O(1)

Best Suited Scenario:

Insertion sort algorithm is best suited with Array and Linked list data structures and the given collection is in partially unsorted order. This algorithm is not feasible for a very large number of data set and this is likely due to its time complexity.

xxxxxxxxxx

function insertionSort(arr) {

    for (let i = 0; i < arr.length; i++) {

        let temp = arr[i];

        let j = i - 1;

        while (j >= 0 && arr[j] > temp) {

            arr[j + 1] = arr[j];

            j = j - 1;

        }

​

        arr[j + 1] = temp;

    }

​

    return arr;

}

​

console.log(insertionSort([1, 3, 6, 7, 4, 8, 9, 1, 4, 6, 7]));

Bubble Sort:

Bubble sort, also categorized as a “comparison-based” sorting algorithm, is a simple sorting algorithm that repeatedly goes through the collection, compares adjacent elements, and swaps them if they are not in sorted order. This is the simplest algorithm and inefficient at the same time. Yet, it is very important to learn about it as it represents the basic foundations of sorting. To perform sorting by this algorithm, the adjacent elements in the collection are compared and the positions are swapped if the first element is greater than the second one. In this way, the largest valued element "bubbles" to the top. Usually, after each loop, the elements furthest to the right are in sorted order. The process is continued until all the elements are in sorted order.

The working of bubble sort algorithm is simulated in below mentioned figure:

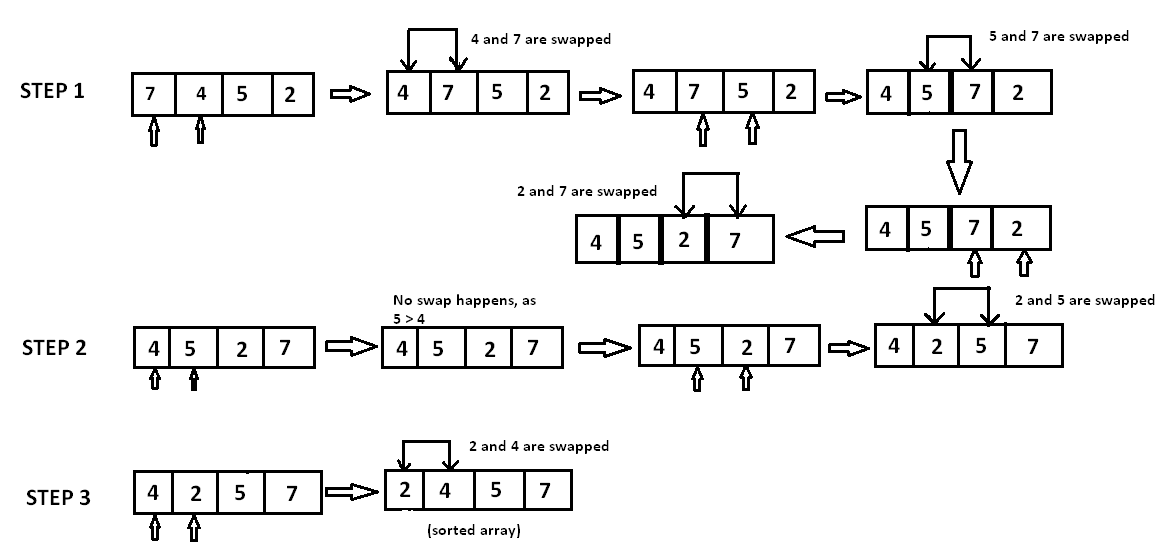
Here's the pseudocode:

1procedure bubbleSort( arr[]: collection of elements, N: size of collection)
2   for i = 0 to N - 1 do:
3      swapped = false	
4      for j = 0 to N - i - 2 do:
5         if arr[j] > arr[j+1] then
6            swap(arr[j], arr[j+1])		
7            swapped = true
8         end if
9      end for
10      if(not swapped) then
11         break
12      end if
13   end for
14end

Time Complexity: O(N2)

Space Complexity: O(1)

Best Suited Scenario:

Bubble sort algorithm is best suited with most of the data structures and the given collection is in completely unsorted order. This algorithm is not feasible for very large number of data set and this is likely due to its time complexity.

xxxxxxxxxx

const bubbleSort = (arr) => {

    for (let i = 0; i < arr.length - 1; i++) {

        for (let j = 0; j < arr.length - 1 - i; j++) {

            if (arr[j] > arr[j+1]) {

                [arr[j], arr[j+1]] = [arr[j+1], arr[j]]

            };

        };

    };

    return arr;

}

​

console.log(bubbleSort([5, 4, 3, 2, 1]));

Merge Sort:

This is a Divide and Conquer algorithm. It divides the input collection into two portions, recursively calls itself for the two divided portions, and then merges the two sorted portions. This is one of the most efficient algorithms. Merge Sort Algorithm works in three parts:

1. Divide: At first, it divides the given collection of elements into two equal halves and then recursively passes these halves to itself.
2. Sorting: Unless, there is only one element left in each half, the division continues, after that, those two end elements (leaf nodes) are sorted.
3. Merging: Finally, the sorted arrays from the top step are merged in order to form the sorted collection of elements

The working of the merge sort algorithm is simulated in below-mentioned figure:

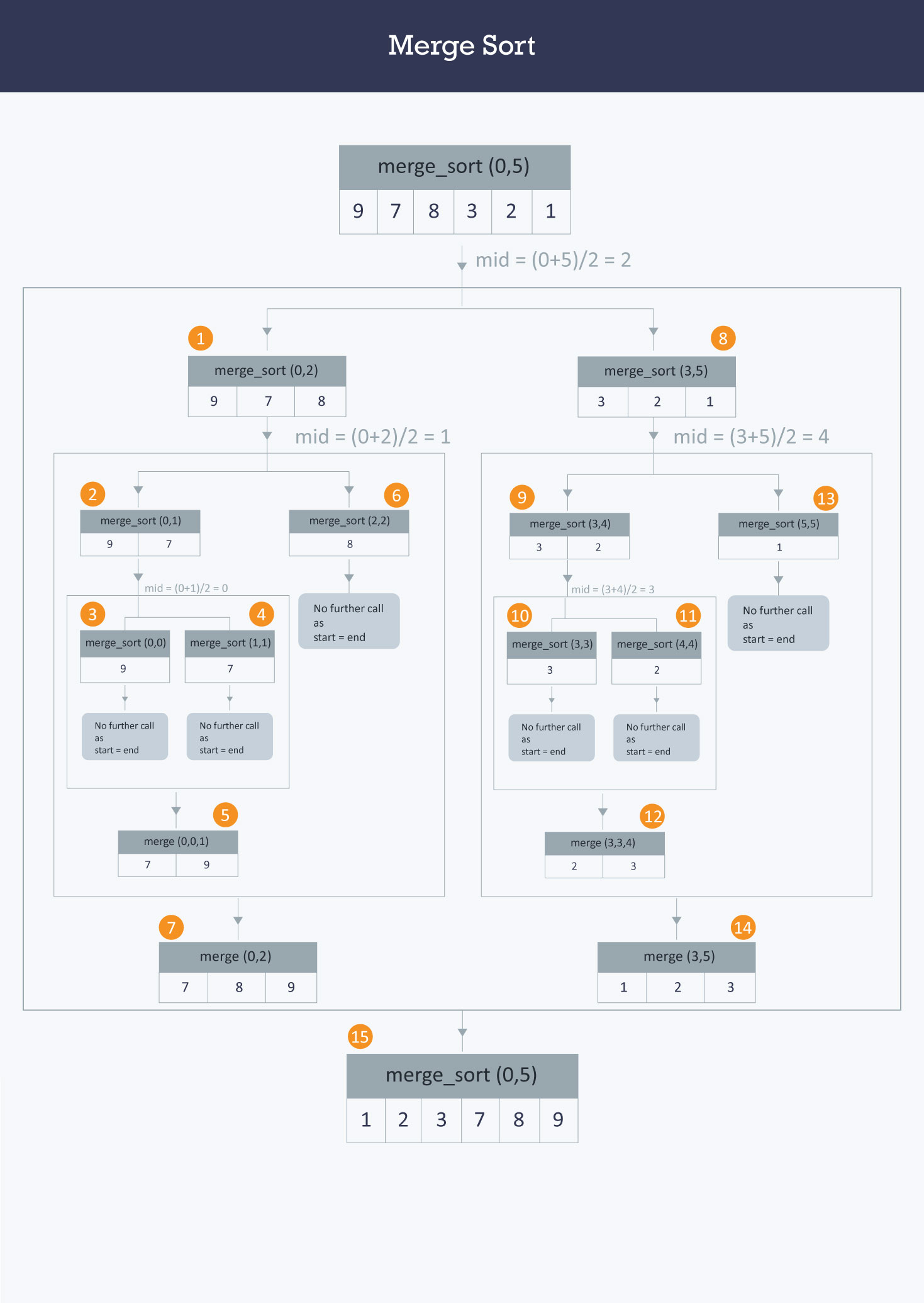
Here's the pseudocode:

1procedure mergesort( var a as array )
2   if ( n == 1 ) return a
3   var l1 as array = a[0] ... a[n/2]
4   var l2 as array = a[n/2+1] ... a[n]
5   l1 = mergesort( l1 )
6   l2 = mergesort( l2 )
7   return merge( l1, l2 )
8end procedure
9
10procedure merge( var a as array, var b as array )
11   var c as array
12   while ( a and b have elements )
13      if ( a[0] > b[0] )
14         add b[0] to the end of c
15         remove b[0] from b
16      else
17         add a[0] to the end of c
18         remove a[0] from a
19      end if
20   end while
21   
22   while ( a has elements )
23      add a[0] to the end of c
24      remove a[0] from a
25   end while
26   
27
28
29   while ( b has elements )
30      add b[0] to the end of c
31      remove b[0] from b
32   end while
33   
34   return c
35end procedure

Time Complexity: O(NlogN)

Space Complexity: O(N)

Best Suited Scenario:

The merge sort algorithm is best suited with most of the data structures and the given collection is in completely unsorted order. This algorithm is feasible for a very large number of data set and this is likely due to its time complexity.

xxxxxxxxxx

console.log(mergeSort([5, 4, 3, 2, 1]));

function merge(leftArr, rightArr) {

  let resultArray = [], leftIndex = 0, rightIndex = 0;

​

  // Sort parts

  while (leftIndex < leftArr.length && rightIndex < rightArr.length) {

    if (leftArr[leftIndex] < rightArr[rightIndex]) {

      resultArray.push(leftArr[leftIndex]);

      leftIndex++; // move left array cursor

    } else {

      resultArray.push(rightArr[rightIndex]);

      rightIndex++; // move right array cursor

    }

  }

​

  // There will be one element remaining from either left or the right

  // Concat to account for it

  return resultArray

          .concat(leftArr.slice(leftIndex))

          .concat(rightArr.slice(rightIndex));

}

​

function mergeSort(unsortedArr) {

  // Only one element base case

  if (unsortedArr.length <= 1) {

    return unsortedArr;

  }

​

  // Determine midpoint

  const midIdx = Math.floor(unsortedArr.length / 2);