Insertion Sort:

This algorithm lies in the category of in-place comparison-based sorting algorithms. In this algorithm, a sub-collection is maintained which is always in order(sorted). For example, the lower part of an array is maintained to be ordered. An element that is to be added in this sorted collection has to find its correct place, and then it has to be inserted there. That’s why the algorithm is named ‘Insertion Sort’.

This sorting algorithm is basically a simple sorting algorithm that works similar to the way you sort the playing cards. The collection is virtually split into an ordered and an unordered part. Elements from the unordered portion are picked and placed at the correct index in the ordered part.

The working of the insertion sort algorithm is simulated in the below-mentioned figure:

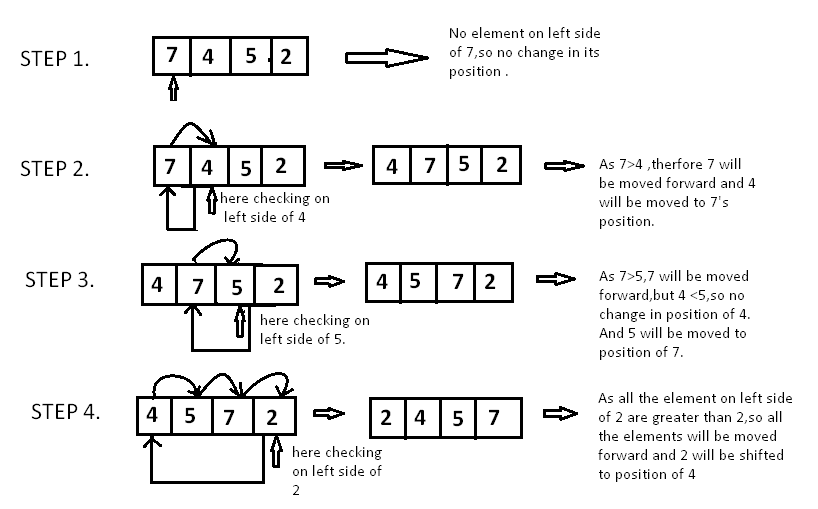
Here's the pseudocode:

1procedure insertionSort( A : collection of items )
2   int holePosition
3   int valueToInsert
4
5   for i = 1 to length(A) inclusive do:
6      /* select value to be inserted */
7      valueToInsert = A[i]
8      holePosition = i
9      /*locate hole position for the element to be inserted */
10      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
11         A[holePosition] = A[holePosition-1]
12         holePosition = holePosition -1
13      end while
14      /* insert the number at hole position */
15      A[holePosition] = valueToInsert
16   end for
17end procedure

Time Complexity: O(N2)

Space Complexity: O(1)

Best Suited Scenario:

Insertion sort algorithm is best suited with Array and Linked list data structures and the given collection is in partially unsorted order. This algorithm is not feasible for a very large number of data set and this is likely due to its time complexity.

xxxxxxxxxx

function insertionSort(arr) {

    for (let i = 0; i < arr.length; i++) {

        let temp = arr[i];

        let j = i - 1;

        while (j >= 0 && arr[j] > temp) {

            arr[j + 1] = arr[j];

            j = j - 1;

        }

​

        arr[j + 1] = temp;

    }

​

    return arr;

}

​

console.log(insertionSort([1, 3, 6, 7, 4, 8, 9, 1, 4, 6, 7]));