AlgoDaily - Cycling Through Cycle Sort

Home > Data Structures and Algorithms 🚀 > Pointers and Windows > Cycling Through Cycle Sort

Step 4: More Swaps and Musical Chairs

Looping Back: Focusing on the Same Index Again

Here comes an interesting twist. Normally, in sorting algorithms, once you're done with an index, you move to the next. But in cycle sort, you'll sometimes stay at the same index for another round. In our case, we haven't moved past index 0 yet; we're still dealing with what's now in that spot, which is 14.

Count, Swap, Repeat: The Sorting Continues

Let's take 14 and do the same counting exercise. How many elements are smaller than 14? Well, all of them! So, 14 should move to the last index, index 5.

Here's how the array transforms:

Before the Swap

The array before the swap:

SNIPPET

1## previous
2idx:       0  1  2  3   4  5
3updated = [14, 4, 6, 8, 9, 3]
4           *

After the Swap

The array after the swap:

SNIPPET

1## updated
2idx:       0  1  2  3   4  5
3updated = [3, 4, 6, 8, 9, 14]
4           ^               ^

Visually Mapping the Swap

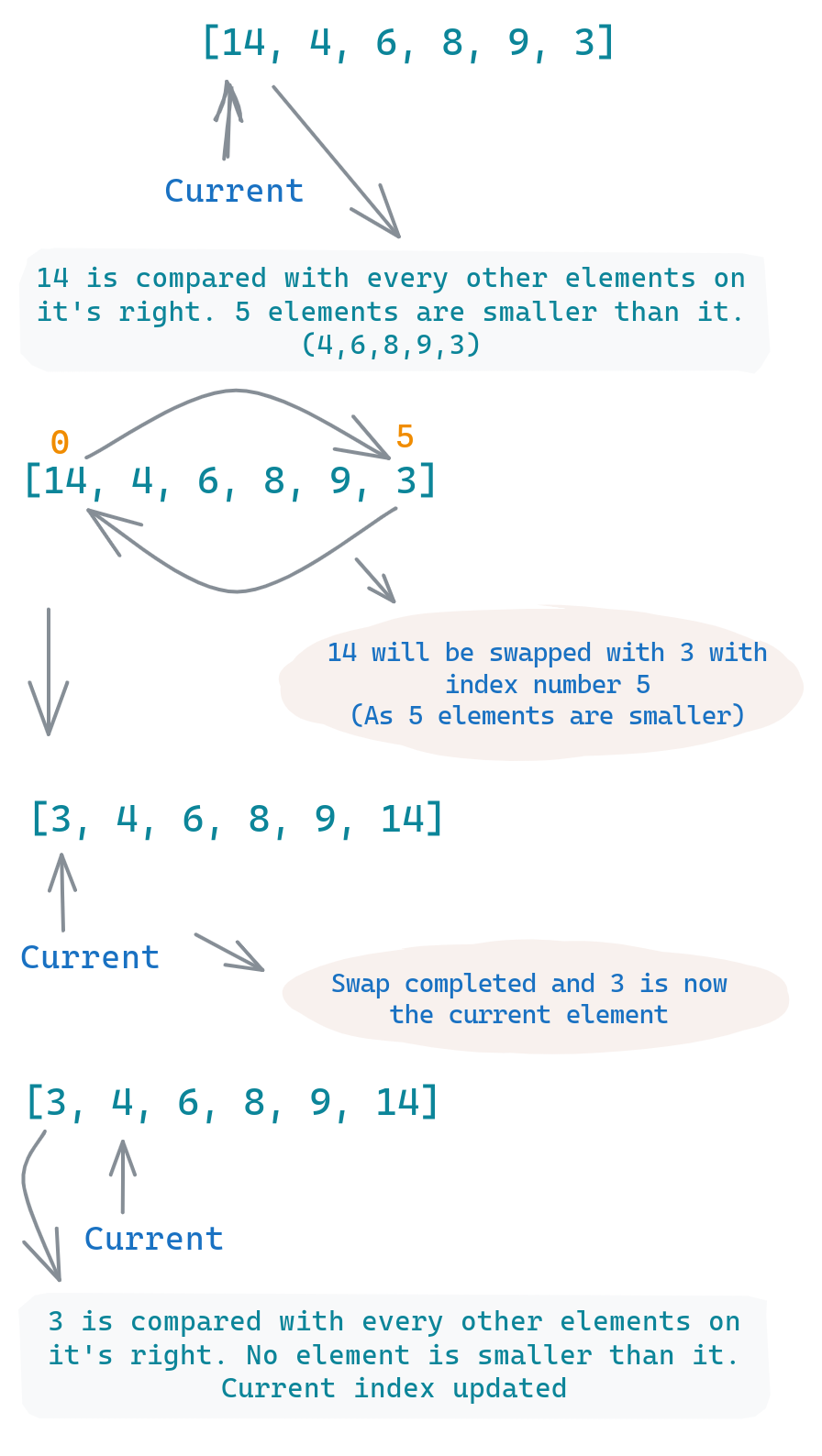
The red arrows in the image above signify the switch. '14' moves to its rightful place at the end of the array, and '3' comes to the front.

Why This Second Swap Matters

You might wonder, why did we not move to the next index? The reason is that the player (number) at the current index hasn't yet found its rightful chair (spot). Only when a player is in its designated chair do we move to the next one. Cycle sort is meticulous like that, ensuring everyone is where they should be, one step at a time. And this iterative refinement is what eventually sorts the entire array.