Notice how beautifully the pseudo-code sorts the array. The outer loop of the algorithm represents a pass of the algorithm. The inner for loop compares consecutive items and swaps them if needed.
The boolean flag sorted is set to true before the inner for-loop for comparing successive items. If no swap is made, it remains true and we can break out of the outer loop.
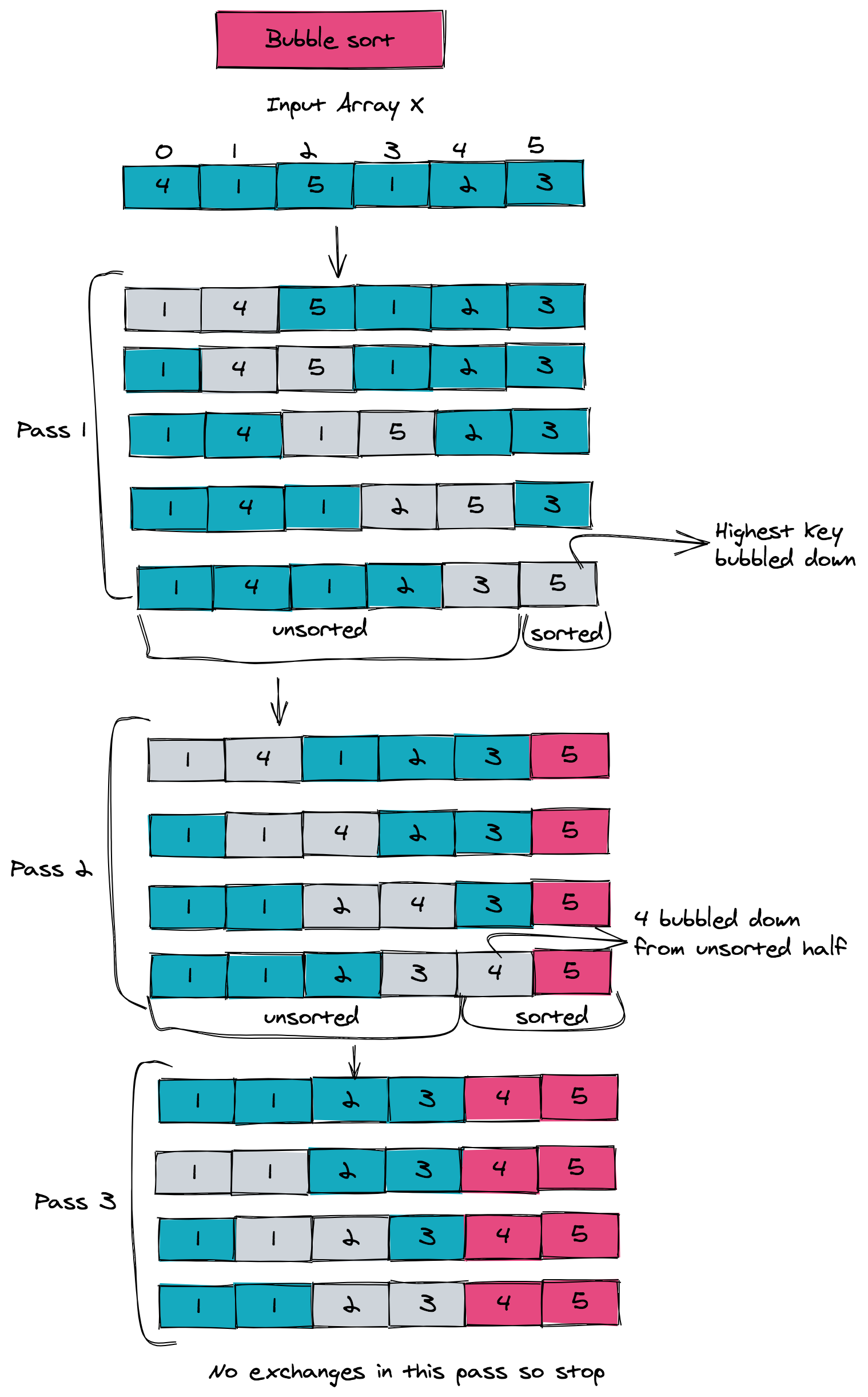
This makes bubble sort a very special algorithm, as it is one of the few sorting algorithms that tells you when an array is sorted. You can stop running further passes if the array is sorted. The entire process is illustrated in the figure below. Notice how the sorted and unsorted parts of the array is maintained, and how the algorithm stops once the array is sorted.
Complexity of Bubble Sort
The time complexity of bubble sort depends upon the input array. As we saw in our pseudo-code, if our array is already sorted, it will make only one pass through the input array. Hence, for a sorted array, its time complexity is O(n). However, in the worst-case scenario, it will make roughly O(n) passes through the array, where each pass is approximately O(n) time. This makes the overall time complexity quadratic, i.e., O(n) in the worst case.
The sorting is in place sorting and does not use any extra array memory. Thus the space complexity is O(1).


