Good morning! Here's our prompt for today.

Here's a classic challenge that comes up in real-life interviews surprisingly often. Interviewers like it as a way to assess your ability to find the right data structure for a non-obvious and non-trivial use case.

The prompt is as follows: you're a university student currently trying to plan their schedule for the following semester. There is n number of courses that you'll need to take to stay on track for graduation.

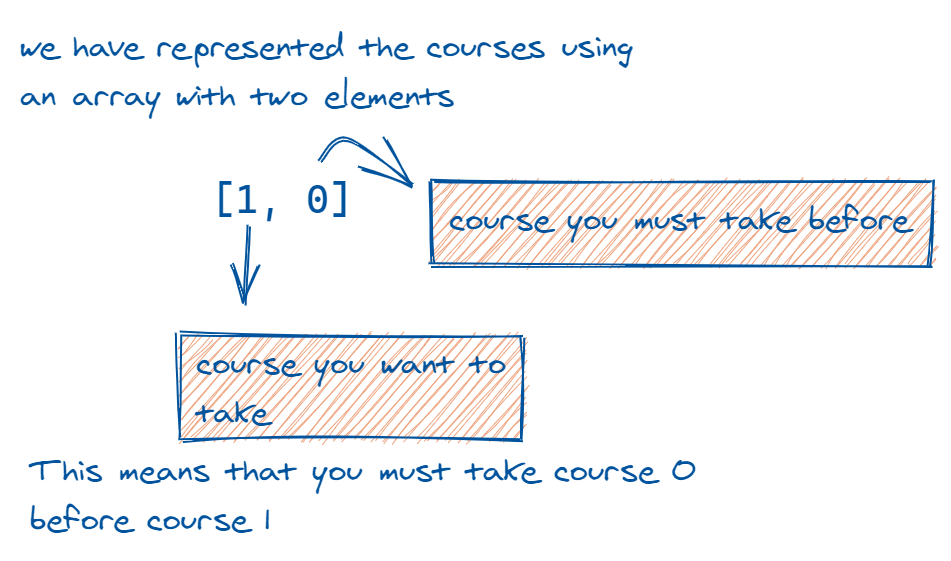
Of the n courses, several have prerequisite courses that you'll need to take beforehand. This requirement is defined using an array with two elements. A prerequisite pair in the form [course, prerequisite] such as [4, 3] means that you need to take course 3 before course 4.

1n = 3
2preReqs = [[1, 0], [2, 1]]
3// You need to take course 0 before 1, and 1 before 2, 
4// but that is an appropriate order.
5// Running areAllCoursesPossible(n, preReqs) would return true.

However, sometimes the prerequisite pairings are not possible-- this will prevent you from staying on track! As an example, if we add an additional prerequisite requirement that you need to finish 2 before 0, it wouldn't work:

1n = 3
2preReqs = [[1, 0], [2, 1], [0, 2]]
3// This is impossible because you can't finish 2 before 0,
4// since you need to finish 1 before 2, and 0 before 1.

In the above, an order of 0 -> 1 -> 2 or 2 -> 1 -> 0 would not fulfill the requirements, so areAllCoursesPossible(n, preReqs) would return false.

Given n and a list of prerequisite pairs, can you write a method to determine if it is possible to take all the courses? Hint: what are the conditions under which a prerequisite setup is impossible?

Constraints

• Number of possible courses <= 100000
• Number of prerequisites <= 100000
• The prerequisites array will always contain the value >= 0
• Expected time complexity : O(V+E) , where V are the courses and E are the prerequisites
• Expected space complexity : O(V)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

​

from collections import defaultdict

​

​

class CourseSchedule:

    def __init__(self):

        self.graph = defaultdict(list)

​

    def add_edge(self, u, v):

        self.graph[u].append(v)

​

    def all_courses_possible(self, num_courses):

        # fill in this method

        return True

​

​

import unittest

​

​

class Test(unittest.TestCase):

    def test_1(self):

        cs = CourseSchedule()

        cs.add_edge(1, 0)

        cs.add_edge(2, 1)

        assert cs.all_courses_possible(3) == True

        print("PASSED: assert CourseSchedule.all_courses_possible(3) == True")

​

    def test_2(self):

        cs = CourseSchedule()

        cs.add_edge(1, 0)

Here's how we would solve this problem...

How do I use this guide?