Good evening! Here's our prompt for today.
Today, we're going to do some math! There is only one prerequisite for answering this question, and it is knowing the definitions of binary and decimal.
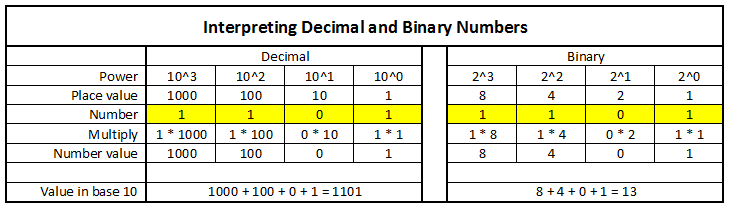
According to How to Convert Decimal to Binary and Binary to Decimal, binary is a numeric system that only uses two digits — 0 and 1. Computers operate in binary, meaning they store data and perform calculations using only zeros and ones.
Decimal, on the other hand, is "a number system that uses a notation in which each number is expressed in base 10 by using one of the first nine integers or 0 in each place and letting each place value be a power of 10."
Can you write a function that returns the binary string of a given decimal number? For example, if the input was 3:
1decimalToBinary(3);
2// 11We get 11 because it is the binary representation of 3 (1 x 2 + 1 x 1).
Constraints
- The given number will be a positive integer in the range between 0 and
1000000000 - Expected time complexity :
O(log n) - Expected space complexity :
O(1)
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxdef decimalToBinary(num): # fill in return numimport unittestclass Test(unittest.TestCase): def test_1(self): assert decimalToBinary(3) == "11" print("PASSED: decimalToBinary(3) should return 11") def test_2(self): assert decimalToBinary(8) == "1000" print("PASSED: decimalToBinary(8) should return 1000") def test_3(self): assert decimalToBinary(1000) == "1111101000" print("PASSED: decimalToBinary(1000) should return 1111101000") def test_4(self): assert callable(decimalToBinary) == True print("PASSED: `decimalToBinary` is a function")if __name__ == "__main__": unittest.main(verbosity=2) print("Nice job, 4/4 tests passed!")We'll now take you through what you need to know.
How do I use this guide?
Converting a Decimal Number to Binary: A Step-by-Step Guide
Converting a decimal number to binary may seem daunting at first, but it can be broken down into a simple, straightforward process. Let's begin with an example!
Here, we will walk through some steps to convert the decimal number 172 to binary using division and recording the remainders. Follow along closely, and you will have your decimal converted to binary in no time! Afterwards, we'll explain what the intuition is behind why this works.
Step 1: Write down the decimal number you wish to convert.
For this example, we will be converting 172 to binary. So let's write down:
172
Step 2: Divide the decimal number by 2.
172 / 2 = 86
Step 3: Record the remainder from Step 2 on the right hand side.
The remainder from dividing 172 by 2 is 0. Let's record this:
172 0
Step 4: Take the result from Step 2, and divide it again by 2.
86 / 2 = 43
Step 5: Record the new remainder from Step 4 on the right hand side, above the previous remainder. The remainder from dividing 86 by 2 is 0. Let's record this:
- 172 0
- 86 0
Step 6: Repeat Steps 4 and 5, dividing the result from Step 4 by 2, and recording the new remainder above, until the result of your division is 0.
Continuing...
- 43 / 2 = 21, remainder 1
- 21 / 2 = 10, remainder 1
- 10 / 2 = 5, remainder 0
- 5 / 2 = 2, remainder 1
- 2 / 2 = 1, remainder 0
- 1 / 2 = 0, remainder 1
So our work will look like:
1172 0
286 0
343 1
421 1
510 0
65 1
72 0
81 1Step 7: The bottom remainder is the Most Significant Bit (MSB), and the top remainder is the Least Significant Bit (LSB).
Step 8: Read the remainders from bottom to top to get the binary representation of the original decimal number.
10101100
And there you have it - the decimal number 172 converted to binary is 10101100 using the division with remainder method. With practice, you'll be a decimal to binary conversion expert! Let us know if you need any clarification on the steps.

Why Does It Work?
The process of converting a decimal number to binary using division and recording the remainders works mathematically because of the way binary and decimal numbers are structured. Here is an explanation:
Binary numbers use only two digits - 0 and 1. Each binary digit represents a power of 2. Starting from the right, the first digit is 2^0, the next is 2^1, then 2^2, and so on.
Decimal numbers represent sums of powers of 10. The rightmost digit is 10^0, the next 10^1, then 10^2, etc.
When we divide a decimal number by 2 repeatedly, recording the remainder each time, we are essentially finding out how many 2s need to be summed to get the original decimal number.
For example, if we start with the decimal 172, visualize each step below as one digit in the final result.
- 172 / 2 = 86 remainder 0 (2^0 = 1)
- 86 / 2 = 43 remainder 0 (2^1 = 2)
- 43 / 2 = 21 remainder 1 (2^2 = 4)
- 21 / 2 = 10 remainder 1 (2^3 = 8)
- 10 / 2 = 5 remainder 0 (2^4 = 16)
- 5 / 2 = 2 remainder 1 (2^5 = 32)
- 2 / 2 = 1 remainder 0 (2^6 = 64)
- 1 / 2 = 0 remainder 1 (2^7 = 128)
So 172 in binary is 10101100 because:
- 1 x (2^7) = 128
- 0 x (2^6) = 0
- 1 x (2^5) = 32
- 0 x (2^4) = 0
- 1 x (2^3) = 8
- 1 x (2^2) = 4
- 0 x (2^1) = 0
- 0 x (2^0) = 0
Which sums to 172.
The division algorithm allows us to repeatedly divide out the largest power of 2 possible to recreate the original decimal number as a sum of powers of 2 - which results in the binary representation.
Let's delve into the coding intricacies of this concept:
Setting the Stage: The Base Case
Picture this: you're given a number, and your mission is to convert it into a binary string. But what if the number is less than 1? In this curious situation, there's no binary string to convert to! So, what do we do? Return an empty string, of course!
1if num < 1:
2 return ''This empty string acts as a foundation for all further calculations.
The Case of the Odd One: num Not Divisible by 2
If your number isn't divisible by 2, it's the odd one out. And odd numbers have that pesky 1 hanging around at the end when converted to binary. How do we deal with it? By making it part of the process!
1if num % 2 > 0:
2 return decimalToBinary((num - 1) // 2) + '1'A Practical Example with 3
If you encounter 3, which is an odd number, the above code snippet will effectively do this:
1. Subtract 1 to get 2.
2. Divide by 2 to get 1.
3. Convert 1 to binary, which is '1'.
4. Add the extra '1' from the odd number at the end.
Result: '11'
The Case of the Even Stevens: num Divisible by 2
If your number is perfectly divisible by 2, it's smooth sailing. Just halve the number and convert what's left into binary.
1if num % 2 == 0:
2 return decimalToBinary(num // 2) + '0'These two conditions form the pillars of our decimal-to-binary conversion function. One handles the odd ones, adding an extra 1 to the binary string. The other tackles the even ones, adding a 0 as they go along.
The Curtain Rises on Time Complexity
Let's talk about the speed of our code. We take our input number n and divide it by 2 until we reach the base case. How many times can you halve a number until you reach the smallest whole number? Well, that's log base 2 of n.
Imagine this as a countdown timer that speeds up every second. It starts slow but gets quicker until it reaches zero. That's logarithmic time for you!
1while n > 0:
2 # perform some operations
3 n = n // 2Unpacking the Space Complexity: A Box of log n Bits
Hold your applause! We're not done yet. What about the space our code occupies?
Well, every time we halve n, we either add a 0 or a 1 to our binary string. Just like our time complexity, we're doing this log base 2 of n times.
1binary_array = []
2while n > 0:
3 binary_array.append(n % 2)
4 n = n // 2The Grand Reveal: O(logn)
Both the time and space complexity of this enchanting algorithm are O(logn).
One Pager Cheat Sheet
- Today's task involves writing a function that converts a decimal number to its binary representation; it requires understanding the definitions of
binaryanddecimal, with the added constraints that the input will be a positive integer between 0 and1000000000, and the expected time and space complexities areO(log n)andO(1)respectively. - The article provides steps to convert a decimal number to binary, using the division with remainder method, by repeatedly dividing by
2and recording the remainders, which, when read from bottom to top, give the binary representation of the original decimal number. - The process of converting a decimal number to binary works by repeatedly dividing the decimal number by
2and recording the remainder, symbolizing the sum of powers of2that construct the original decimal number, yielding the binary representation. - The text outlines a coding approach to convert decimal numbers to binary, specifying that if a number is less than
1, an empty string should be returned and detailing two cases: ifnumis divisible by2, and if it's not, whereby recursive operations are performed; the time and space complexity of this approach isO(logn).
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx print("Nice job, 4/4 tests passed!")def decimalToBinary(num): binaryNum = [] binary = "" while num > 0: remainder = num % 2 binaryNum.append(remainder) num = int(num / 2) for i in range(len(binaryNum) - 1, -1, -1): binary += str(binaryNum[i]) return binaryimport unittestclass Test(unittest.TestCase): def test_1(self): assert decimalToBinary(3) == "11" print("PASSED: decimalToBinary(3) should return 11") def test_2(self): assert decimalToBinary(8) == "1000" print("PASSED: decimalToBinary(8) should return 1000") def test_3(self): assert decimalToBinary(1000) == "1111101000" print("PASSED: decimalToBinary(1000) should return 1111101000") def test_4(self): assert callable(decimalToBinary) == TrueGot more time? Let's keep going.
If you had any problems with this tutorial, check out the main forum thread here.


