Good morning! Here's our prompt for today.
Can you detect a cycle in an undirected graph? Recall that an undirected graph is one where the edges are bidirectional. A cycle is one where there is a closed path, that is, the first and last graph vertices can be the same.
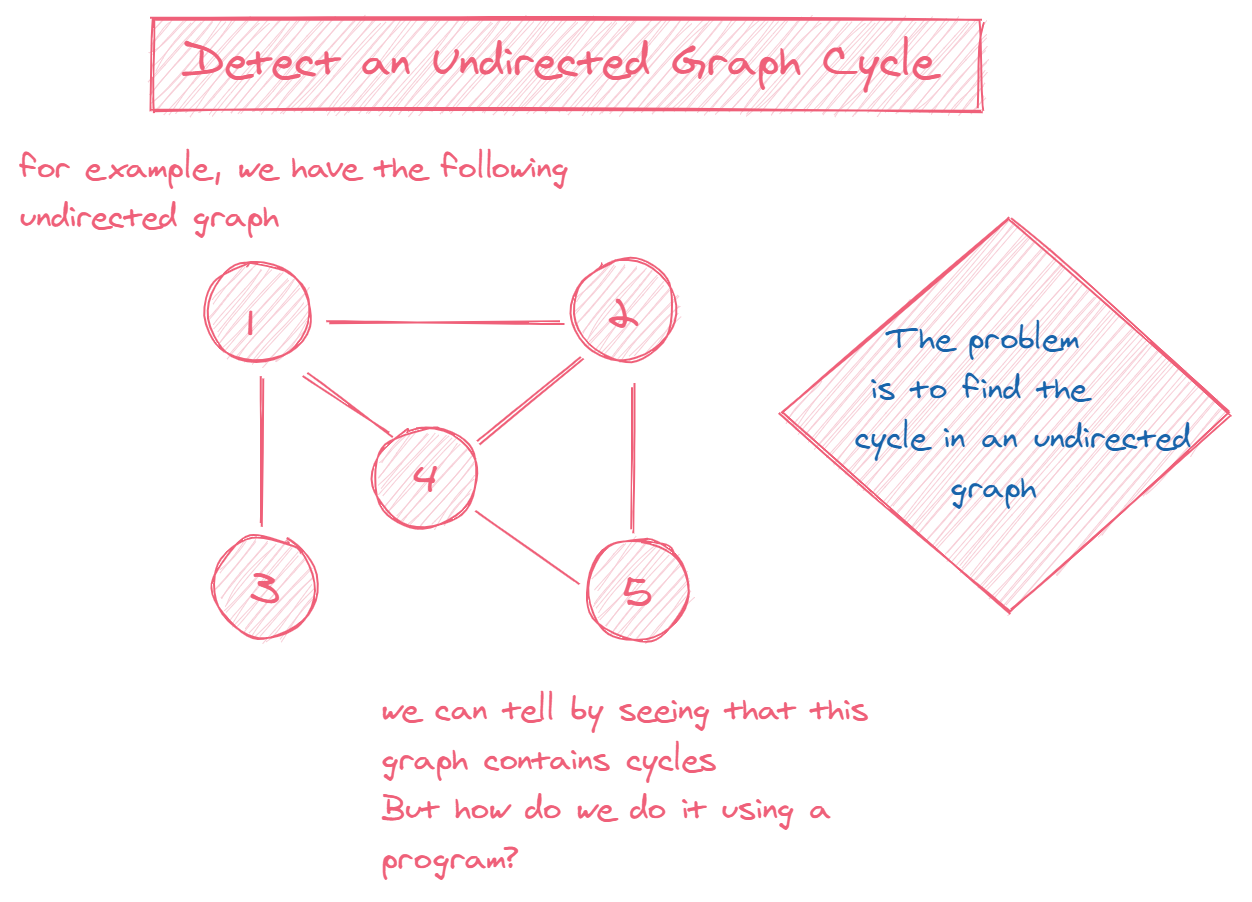
We've covered how to detect a cycle using depth-first search, but can you find one without it? Assume the following graph definition:
JAVASCRIPT
1class Graph {
2 constructor() {
3 this.adjacencyList = new Map();
4 }
5
6 addVertex(nodeVal) {
7 this.adjacencyList.set(nodeVal, []);
8 }
9
10 addEdge(src, dest) {
11 this.adjacencyList.get(src).push(dest);
12 this.adjacencyList.get(dest).push(src);
13 }
14
15 removeVertex(val) {
16 if (this.adjacencyList.get(val)) {
17 this.adjacencyList.delete(val);
18 }
19
20 this.adjacencyList.forEach((vertex) => {
21 const neighborIdx = vertex.indexOf(val);
22 if (neighborIdx >= 0) {
23 vertex.splice(neighborIdx, 1);
24 }
25 });
26 }
27
28 removeEdge(src, dest) {
29 const srcDestIdx = this.adjacencyList.get(src).indexOf(dest);
30 this.adjacencyList.get(src).splice(srcDestIdx, 1);
31
32 const destSrcIdx = this.adjacencyList.get(dest).indexOf(src);
33 this.adjacencyList.get(dest).splice(destSrcIdx, 1);
34 }
35}Constraints
- The number of vertices in the graph <=
100000 - The number of edges in the graph <=
100000 - Let
|V|,|E|represent the number of vertices and edges of the graph - Expected time complexity :
O(|V|+|E|) - Expected space complexity :
O(|V|)
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxx67
from collections import defaultdict# This class represents a undirected graph using# adjacency list representationclass Graph: def __init__(self, vertices): self.V = vertices # number of vertices # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A utility function to find the subset of an element i def find_parent(self, parent, i): if parent[i] == -1: return i if parent[i] != -1: return self.find_parent(parent, parent[i]) # A utility function to do union of two subsets def union(self, parent, x, y): x_set = self.find_parent(parent, x) y_set = self.find_parent(parent, y) parent[x_set] = y_setOUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment
We'll now take you through what you need to know.
How do I use this guide?
Access all course materials today
The rest of this tutorial's contents are only available for premium members. Please explore your options at the link below.


