Good morning! Here's our prompt for today.

In the official React documentation, it's recommended that to find out where state data should live, the following steps be taken:

• Identify every component that renders something based on that state.
• Find a common owner component (a single component above all the components that need the state in the hierarchy).
• Either the common owner or another component higher up in the hierarchy should own the state.

This is an algorithmic problem-- let's find the lowest common ancestor!

You're given a binary search tree tree1 and two of its child nodes as parameters. Can you write a method lowestCommonAncestor(root: Node, node1: Node, node2: Node) to identify the lowest common ancestor of the two nodes? The lowest common ancestor is the deepest node that has both of the two nodes as descendants.

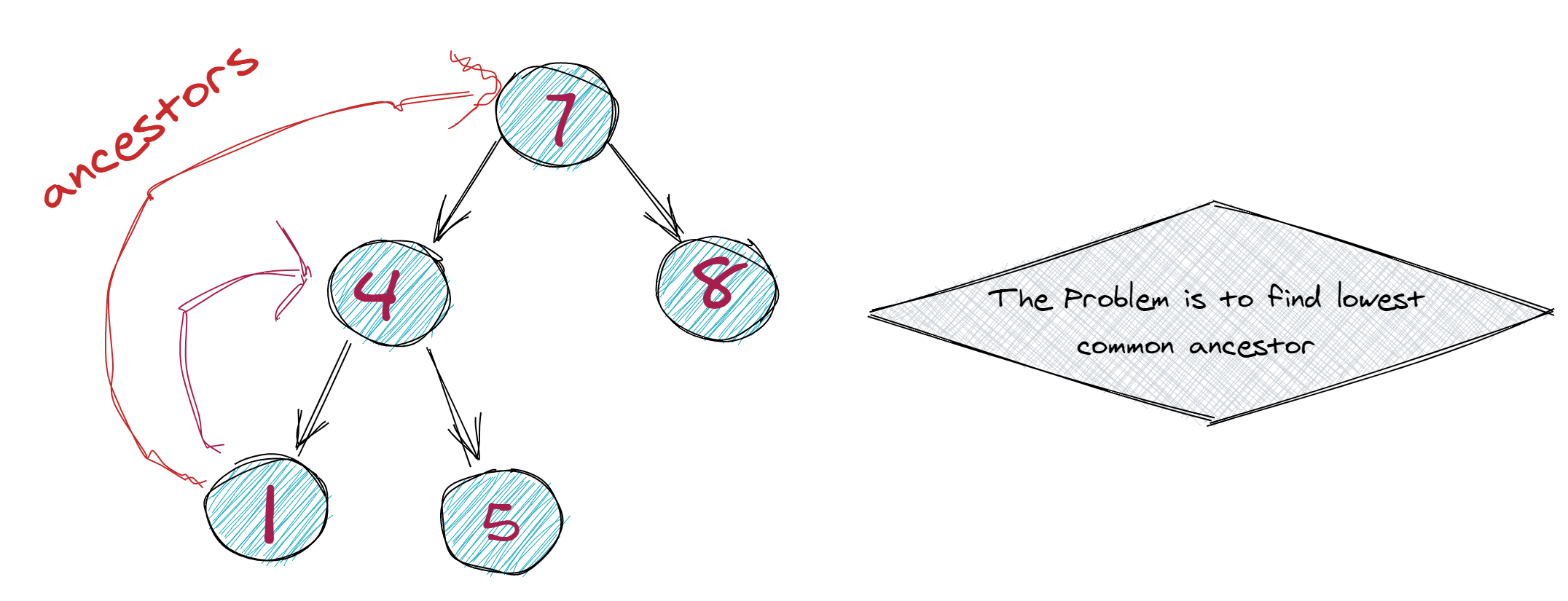
In the below example, the lowest common ancestor of node 5 and 8 is 7.

1/*
2       7
3      / \
4     4   8
5    / \
6   1   5
7*/

The method will called in the following manner: lowestCommonAncestor(root, node1, node2);.

You can assume our standard node definition for the tree vertices:

1// Node definition
2function Node(val) {
3  this.val = val;
4  this.left = this.right = null;
5}

Bonus: is there a way to find the lowest common ancestor of two nodes if the root wasn't passed as a parameter?

Constraints

• Number of nodes in the BST <= 1000
• The nodes will always contain integer values between -1000000000 and 1000000000
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  console.log('PASSED: ' + '`lowestCommonAncestor` should be a function');

var assert = require('assert');

​

function lowestCommonAncestor(root, node1, node2) {

  // Fill in this method

  return root;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

​

var tree4 = new Node(5);

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?