Good evening! Here's our prompt for today.

In the official React documentation, it's recommended that to find out where state data should live, the following steps be taken:

• Identify every component that renders something based on that state.
• Find a common owner component (a single component above all the components that need the state in the hierarchy).
• Either the common owner or another component higher up in the hierarchy should own the state.

This is an algorithmic problem-- let's find the lowest common ancestor!

You're given a binary search tree tree1 and two of its child nodes as parameters. Can you write a method lowestCommonAncestor(root: Node, node1: Node, node2: Node) to identify the lowest common ancestor of the two nodes? The lowest common ancestor is the deepest node that has both of the two nodes as descendants.

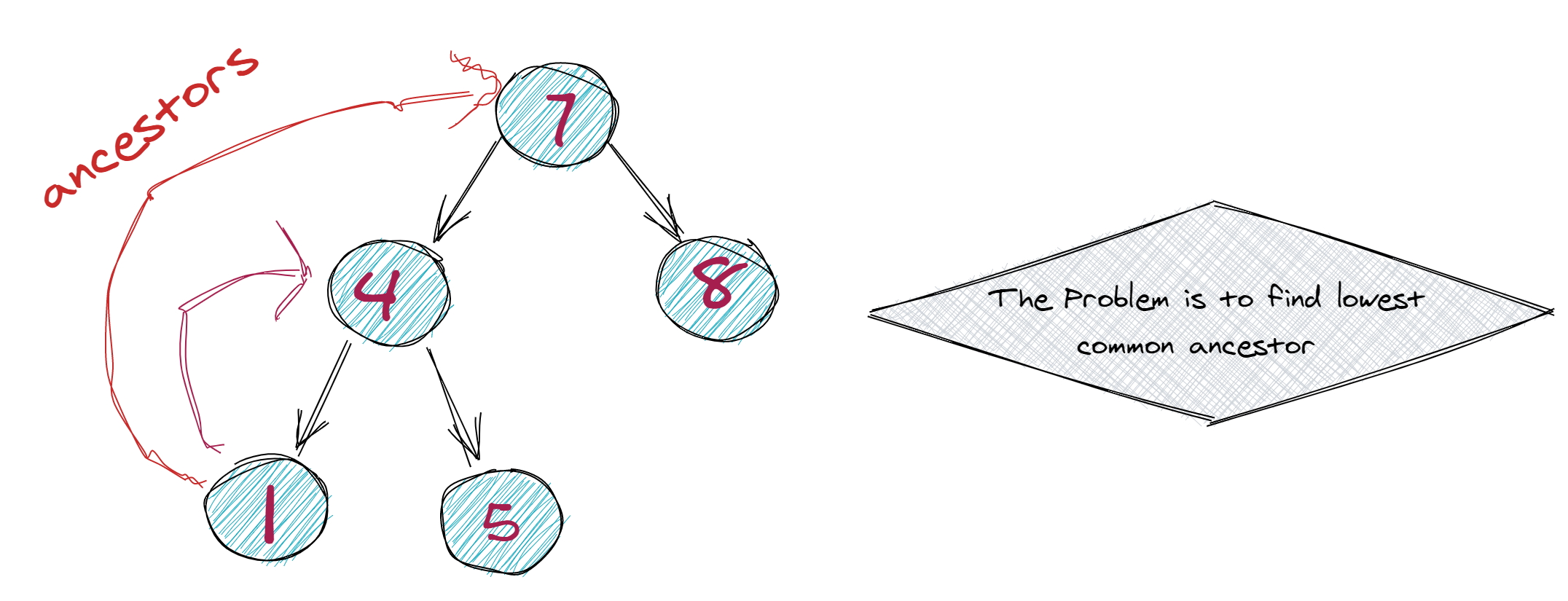
In the below example, the lowest common ancestor of node 5 and 8 is 7.

1/*
2       7
3      / \
4     4   8
5    / \
6   1   5
7*/

The method will called in the following manner: lowestCommonAncestor(root, node1, node2);.

You can assume our standard node definition for the tree vertices:

1// Node definition
2function Node(val) {
3  this.val = val;
4  this.left = this.right = null;
5}

Bonus: is there a way to find the lowest common ancestor of two nodes if the root wasn't passed as a parameter?

Constraints

• Number of nodes in the BST <= 1000
• The nodes will always contain integer values between -1000000000 and 1000000000
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  console.log('PASSED: ' + '`lowestCommonAncestor` should be a function');

var assert = require('assert');

​

function lowestCommonAncestor(root, node1, node2) {

  // Fill in this method

  return root;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

​

var tree4 = new Node(5);

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

The problem could be initially intimidating if you've never heard of the term lowest common ancestor. However, once you realize that it's just the highest shared parent that two nodes have in common, it's easy to visualize ways to use some form of traversal to our advantage.

One way to go about this problem is to visualize the traversal path required from the leaves. We'd probably want to move towards the top since that's where the ancestor is. In other words, we would follow the nodes upwards to get to the lowest common ancestor. This means if we wanted to find the LCA of 2 and 9 below, we'd first trace 2 upwards (so the path followed goes 2 -> 4 -> 6).

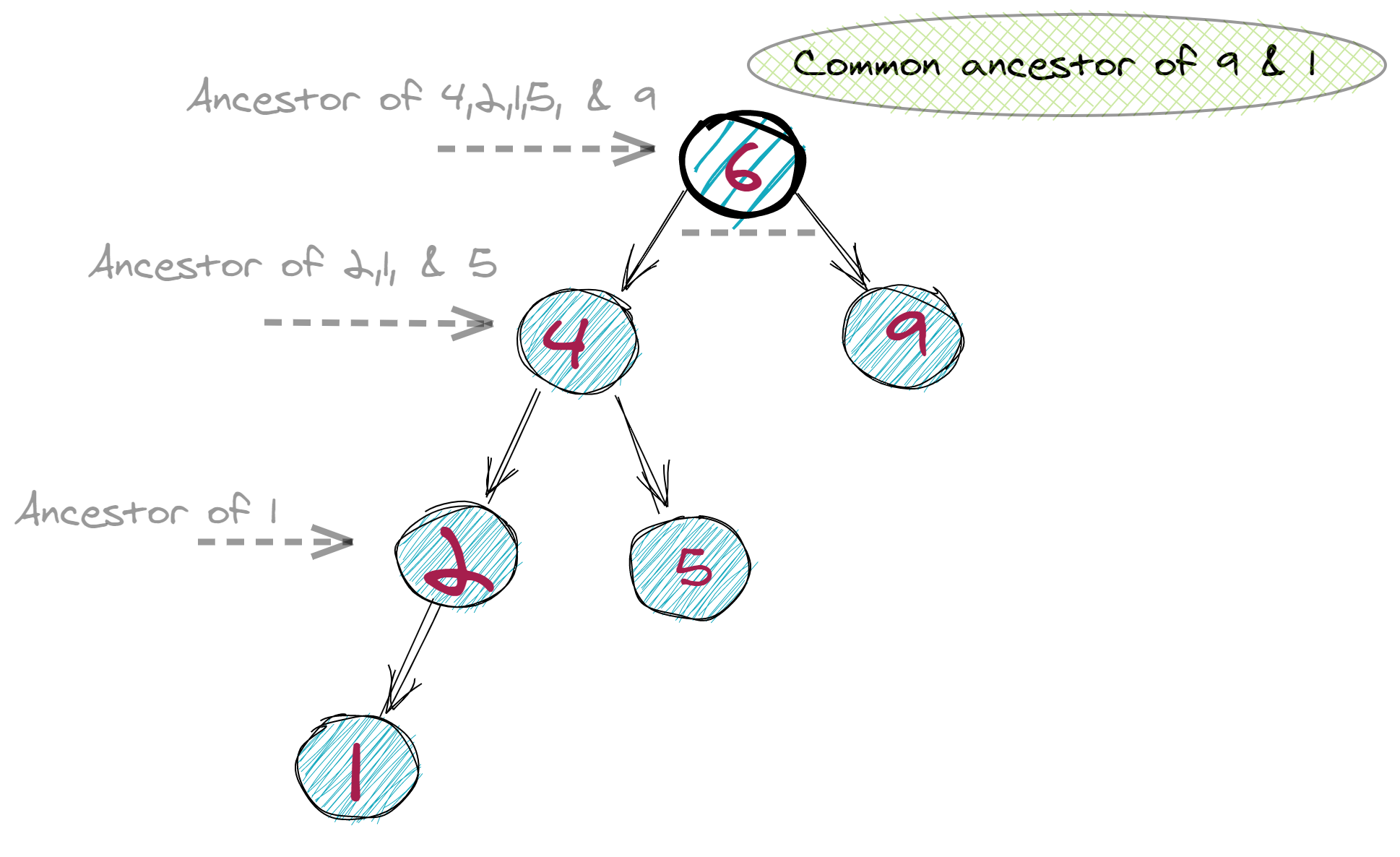
xxxxxxxxxx

/*

       6 

      / \ 

     4   9 

    / \

   2   5

  / \

 1   3

*/

Then, we'd repeat this for 9 (9 -> 6).

See something in common? The final nodes of both paths ended up being the same (node 6). We are thus able to conclude that 6 is the lowest common ancestor, as it's by definition the highest node they have in common (note that there can more than one shared ancestor, but this is the lowest in the branching chain).

If we think about possible solutions, what do we need to do? The solution we want is a traversal to find the first difference in node-to-root path. Is there anything about BST properties that could help us traverse upwards while starting from the root?

Let's revisit some Binary Search Tree properties and start with a basic question about binary trees:

Look at this BST, and let's say we're looking for 4 and 8's LCA:

xxxxxxxxxx

/*

   7

  / \

 4   8

*/

From top to bottom, notice that 7 is between 4 and 8, as the structure follows the normal properties of a BST. We can express that idea with this conditional: if we encounter a node between node1 and node2, it means that it is a common ancestor of node1 and node2.

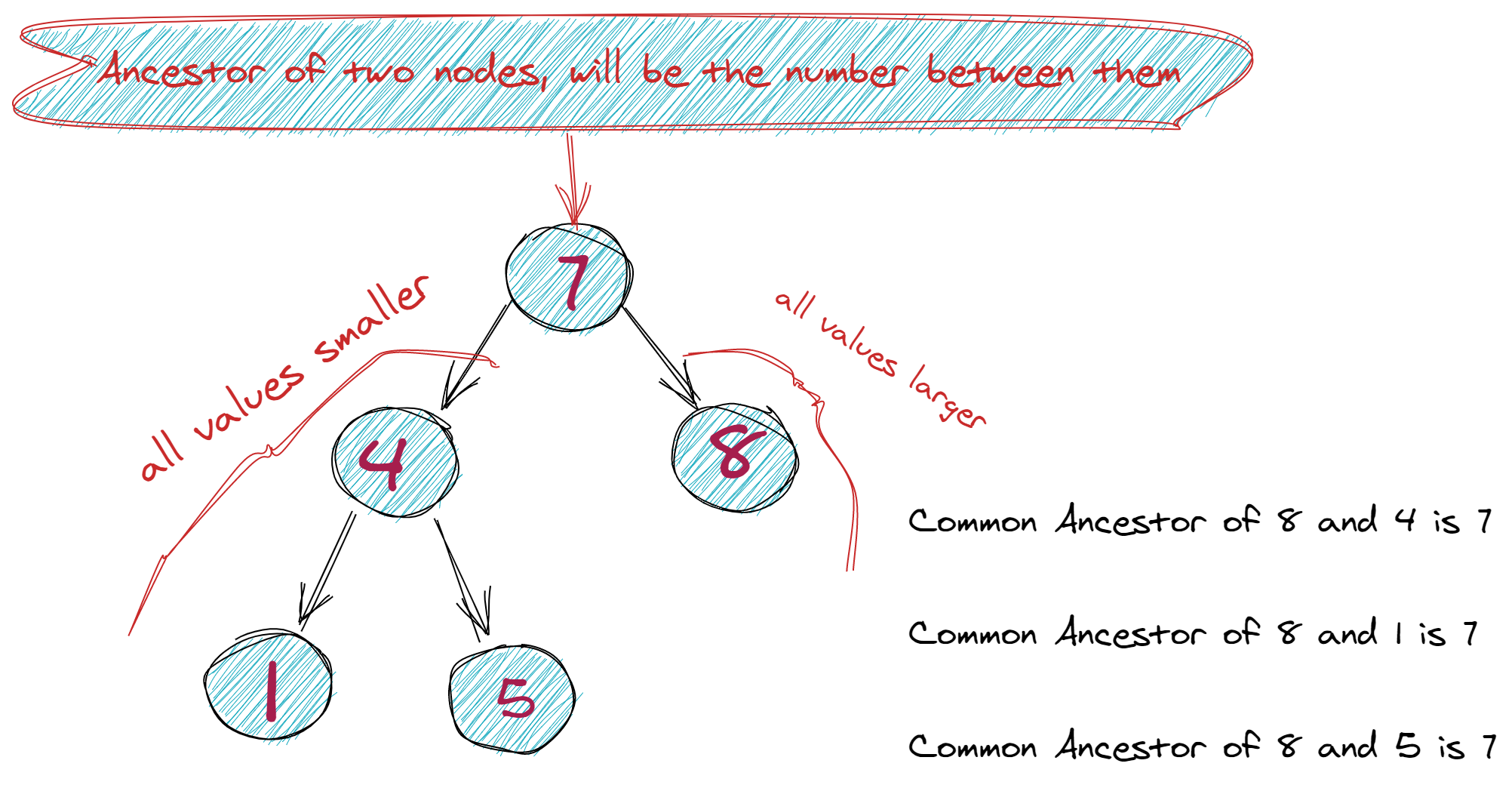
It also spawns these two ideas: if we encounter a node greater than both the nodes, we're going to find our lowest common ancestor on its left side. Likewise, if we encounter a node smaller than both the nodes, we're going to find our lowest common ancestor on its right side.

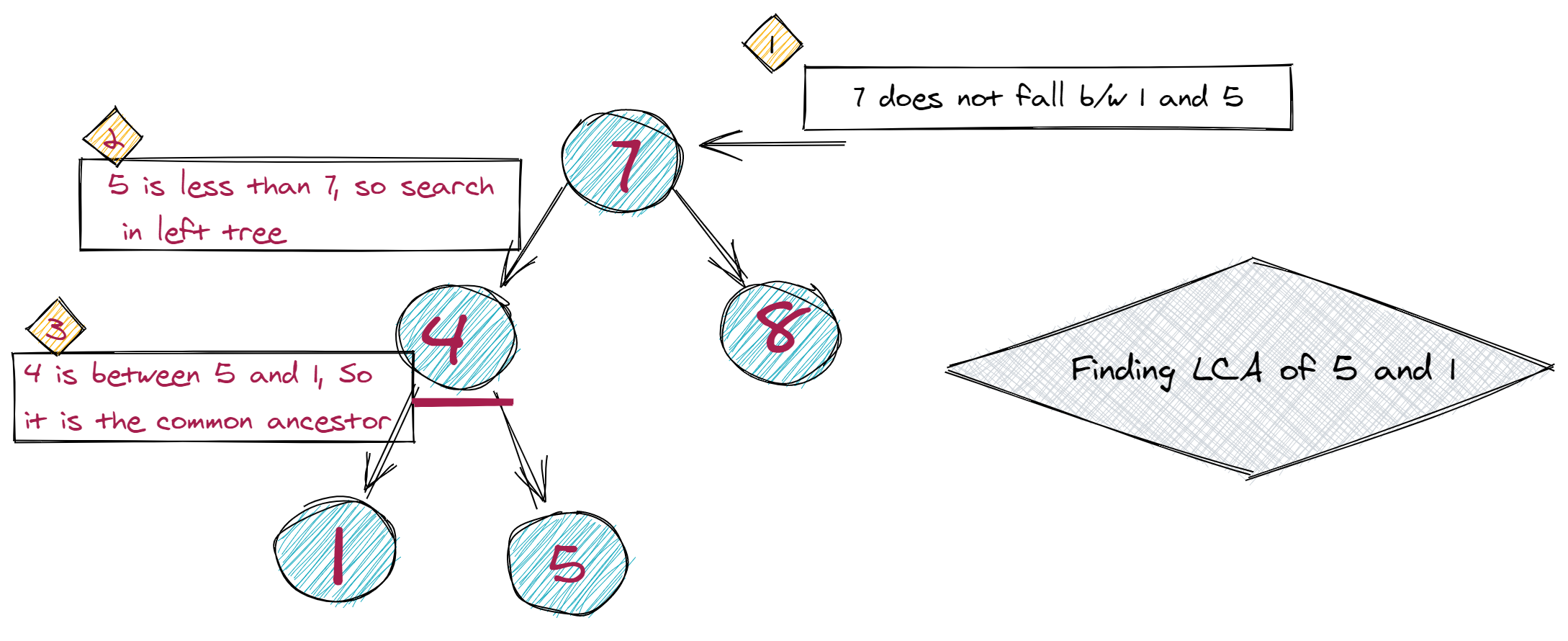
Why is that? Let's see the tree expanded a bit.

xxxxxxxxxx

/*

      7

     / \

    4   8

   / \

  1  5

*/

We'd like to find the LCA of 1 and 8. So start from 7, and compare 7 to 1 (greater) and 8 (less). It's in between, so we know it's the LCA!

What if we were looking to find the LCA of 1 and 5 instead?. Starting from 7, if we compare 7 to 1, it's greater. But 7 is ALSO greater than 5 -- it's greater than both.

That indicates that, from 7, we want to traverse left since we're currently to the right of both nodes.

xxxxxxxxxx

class TreeNode {

    constructor(val, left = null, right = null) {

        this.val = val;

        this.left = left;

        this.right = right;

    }

}

​

function leastCommonAncestor(root, node1, node2) {

    if (root.val > node1 && root.val > node2) {

        return leastCommonAncestor(root.left, node1, node2);

    } else if (root.val < node1 && root.val < node2) {

        return leastCommonAncestor(root.right, node1, node2);

    } else {

        return root;

    }

}

​

const root = new TreeNode(6);

root.left = new TreeNode(2);

root.right = new TreeNode(8);

root.left.left = new TreeNode(0);

root.left.right = new TreeNode(4);

root.right.left = new TreeNode(7);

root.right.right = new TreeNode(9);

console.log(leastCommonAncestor(root, 2, 8).val);

Here's how you could test out the previous code using another example input:

xxxxxxxxxx

console.log(leastCommonAncestor(root, 1, 8).val);

class Node {

    constructor(val) {

        this.val = val;

        this.left = null;

        this.right = null;

    }

}

​

function leastCommonAncestor(root, node1, node2) {

    if (root.val > node1 && root.val > node2) {

        return leastCommonAncestor(root.left, node1, node2);

    } else if (root.val < node1 && root.val < node2) {

        return leastCommonAncestor(root.right, node1, node2);

    } else {

        return root;

    }

}

​

//       7

//      / \

//     4   8

//    / \

//   1  5

​

const root = new Node(7);

root.left = new Node(4);

root.left.left = new Node(1);

root.left.right = new Node(5);

root.right = new Node(8);

We can alternatively use an iterative approach.

Let's put it all together:

xxxxxxxxxx

console.log(lowestCommonAncestor(root, 1, 8));

function lowestCommonAncestor(root, node1, node2) {

  // instantiate 2 arrays to keep track of paths

  const path1 = [];

  const path2 = [];

​

  // obtain the paths of each node from root

  if (!getPath(root, path1, node1) || !getPath(root, path2, node2)) {

    return false;

  }

​

  let i = 0;

  // compare the two until they differentiate or we hit the end

  while (i < path1.length && i < path2.length) {

    if (path1[i] != path2[i]) {

      break;

    }

    i++;

  }

​

  return path1[i - 1];

​

  function getPath(root, path, k) {

    if (!root) {

      return false;

    }

​

    // basic DFS

    path.push(root.val);

​