Good afternoon! Here's our prompt for today.

Merging Two Binary Trees

The Problem Statement

You are presented with two binary trees. Your task is to merge these trees into a single, new binary tree.

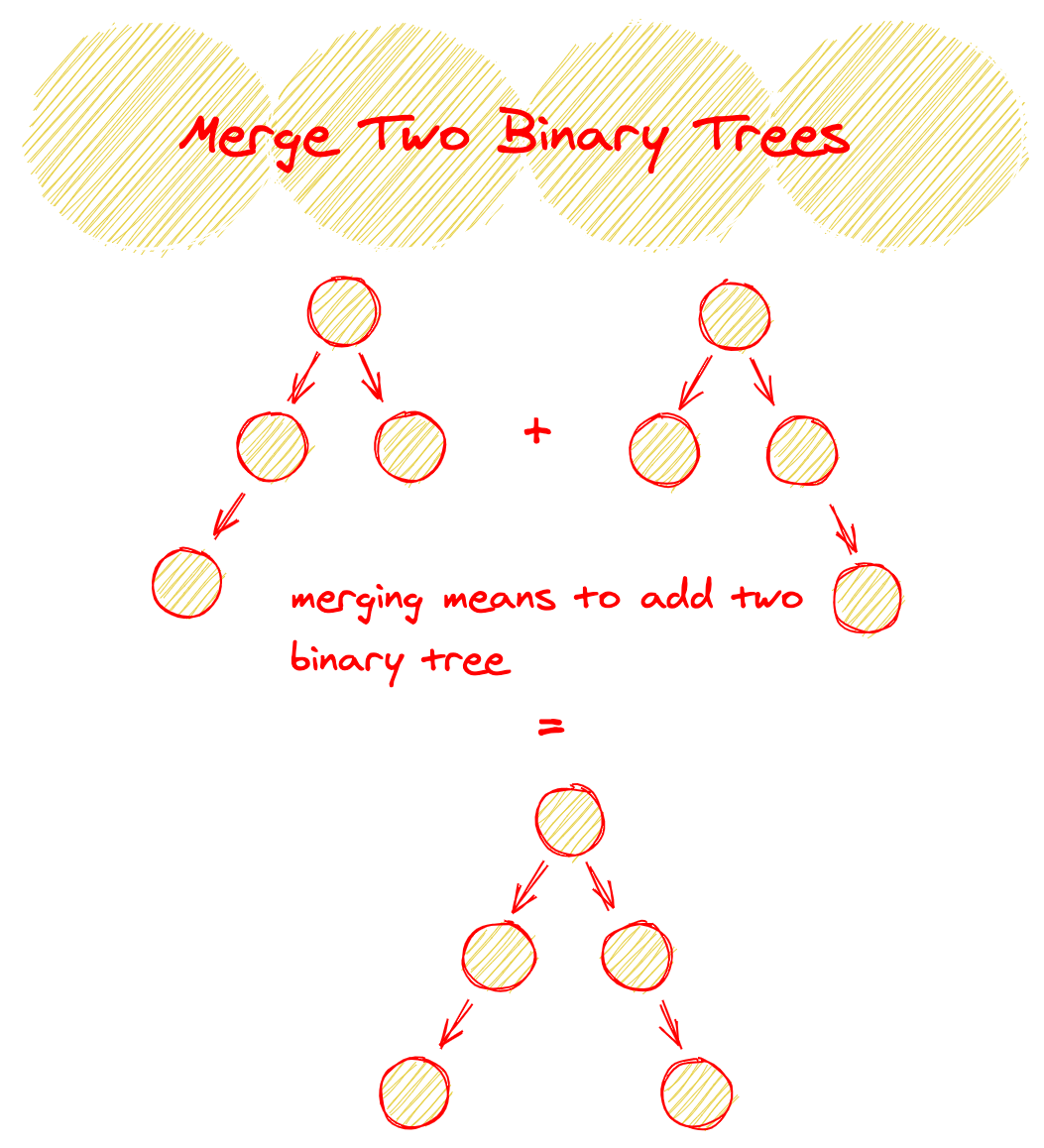
The Overlap Rule

Here's the catch: some nodes in these two trees may overlap when you try to put them together. When that happens, the new node's value in the merged tree will be the sum of the overlapping nodes. For instance, consider the right leaf node in Tree 1 with a value of 2 and the right node in Tree 2 with a value of 3. In the merged tree, the corresponding node would have a value of 5 (2 + 3).

The No-Overlap Rule

If nodes don't overlap, the node value from the existing tree is simply carried over into the new tree.

An Example to Illuminate

Here's a quick example to make this more concrete:

TEXT

1  Tree 1                 Tree 2         
2    1                       2               
3   / \                     / \              
4  3   2                   1   3             
5 /                         \   \            
65                           4   7           
7
8Resulting Merged Tree:
9    3
10   / \
11  4   5
12 / \   \ 
135   4   7

Boilerplate Code

You can assume that the nodes in the tree are defined as follows in JavaScript:

JAVASCRIPT

1function Node(val) {
2  this.val = val;
3  this.left = this.right = null;
4}

Constraints and Expectations

Both trees will contain no more than 100,000 nodes.
Node values will always be integers and fall in the range -1,000,000,000 to 1,000,000,000.
Aim for a time complexity of (O(m+n)), where (m) and (n) are the number of nodes in each of the binary trees, respectively.

Your task is to start merging from the root nodes of both trees and produce a new tree that satisfies the above conditions.

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
# class Node:
#   def __init__(val):
#     this.val = val
#     this.left = None
#     self.right = None
​
​
def merge_two_binary_trees(tree1, tree2):
    # fill in
    return tree1
​
​
# Node definition
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
​
​
# Regular binary trees
tree1 = Node(4)
tree1.left = Node(1)
tree1.right = Node(3)
​
tree2 = Node(5)
tree2.left = Node(10)
tree2.left.left = Node(17)
tree2.left.right = Node(3)

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

Unveiling the Approach: Merging Binary Trees

Step 1: The Simple Case - Merging Root Nodes

Before diving into the complexities of merging full-fledged binary trees with all their branches and leaves, let's start simple. We'll consider the most basic case: two trees each containing only a root node.

Here's the example we'll work through:

TEXT

1  1st Tree         2nd Tree         Merged Tree       
2      3               1                  4

The Strategy for Merging Root Nodes

Check for Empty Trees: First, ensure that neither of the root nodes is null.
Sum the Values: If both roots exist, sum their values to create a new root node for the merged tree.
Create the Merged Root: Instantiate a new node with the sum as its value.

Code Snippet for Merging Root Nodes

Here's how you would implement these steps.

Great! We've successfully merged two single-node trees. But what happens when these trees have children?

xxxxxxxxxx
 
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
​
def merge_trees(root1, root2):
    # Check for empty trees
    if not root1:
        return root2
    if not root2:
        return root1
    
    # Sum the root nodes' values
    sum_val = root1.val + root2.val
    
    # Create the merged root
    merged_root = Node(sum_val)
    
    return merged_root
​
# Create individual root nodes for 1st and 2nd trees
root1 = Node(3)
root2 = Node(1)
​
# Merge and get the new root
merged_root = merge_trees(root1, root2)
print(f"Merged Root Value: {merged_root.val}")  # Output should be 4

The Human Approach to Merging Trees

Imagine you have two different trees. To combine them into one tree, you'd naturally start by looking at the top piece of each puzzle—the root. You'd combine these roots to create a new root for the merged tree.

Then, you'd proceed down each branch, combining corresponding pieces (nodes) from each tree. If a branch exists in one tree but not the other, you'd simply include the existing branch in the new tree. If a branch exists in both trees, you'd combine them to form a new branch.

Running Through Examples to Identify Patterns

Example 1

Tree 1: A single node with value 3
Tree 2: A single node with value 1
Merged Tree: A single node with value (3 + 1 = 4)

Example 2

Tree 1:
- Root: 3
- Left child: 5
Tree 2:
- Root: 1
- Right child: 4
Merged Tree:
- Root: (3 + 1 = 4)
- Left child: 5 (from Tree 1)
- Right child: 4 (from Tree 2)

Example 3

Tree 1:
- Root: 2
- Left child: 3
- Right child: 4
Tree 2:
- Root: 1
- Left child: 4
- Right child: 5
Merged Tree:
- Root: (2 + 1 = 3)
- Left child: (3 + 4 = 7)
- Right child: (4 + 5 = 9)

Observations

Roots Merge: The root of the merged tree is the sum of the roots of the individual trees.
Branching Logic: If a node exists in one tree but not in the other, the node from the existing tree is included in the merged tree.
Recursive Nature: The process for merging the children of two nodes looks suspiciously similar to the process for merging the roots. This suggests a recursive solution.

Armed with these observations, we can confidently proceed to code our brute-force solution.

Build your intuition. Fill in the missing part by typing it in.

Complete the sentence. The merge rule is: if two nodes overlap, the resultant node is the _ of the two nodes.

Write the missing line below.

Try this exercise. Is this statement true or false?

True or False? The merging step does not have to start from the root nodes of both trees.

Press true if you believe the statement is correct, or false otherwise.

Visualizing the Merging Process

The picture truly is worth a thousand words. In this diagram, we see Tree 1 with a root node of 3 and Tree 2 with a root node of 1. As per our observation #1—"Roots Merge"—we combine these roots to create a new root for the merged tree, which has a value of (3 + 1 = 4).

The Steps in the Process

Start at the Roots: We begin with the root nodes of both Tree 1 and Tree 2. These are 3 and 1, respectively.
Merge the Roots: We add the values of these root nodes together. (3 + 1 = 4)
Create the Merged Root: We then use this sum to create the root node of our new, merged tree.

xxxxxxxxxx
 
/*
  1st Tree            2nd Tree           Merged Tree            
      3                  1                    4   
     / \                / \                  / \        
    1                  3                    4        
*/

Moving Down to the Left Child Node

Excellent! We've successfully merged the root nodes. Now, it's time to move on to the children nodes, starting with the left child. Just as we merged the root nodes, we'll use the same strategy for the children nodes.

A Step-by-Step Look

Locate the Left Children: Per the current example, let's assume that Tree 1 has a left child with a value of 1, and Tree 2 has a left child with a value of 3.
Merge the Left Children: As with the roots, we sum the values of these left children nodes. (1 + 3 = 4)
Create the Merged Left Child: This sum becomes the value of the new left child node in our merged tree.

Result of the Operation

By following these steps, we end up with a merged tree that has a root node of 4 and a left child node of 4.

The Recursive Nature

What's nice about this process is its inherently recursive nature. Once we've figured out how to merge the root and one set of children nodes, we can apply the same logic to all subsequent layers of the tree. This sets us up perfectly for the coding phase, where recursion will help us elegantly navigate and merge the trees.

Are you sure you're getting this? Click the correct answer from the options.

How many parameters does the merge tree function need to perform a merger?

Click the option that best answers the question.

Let's test your knowledge. Click the correct answer from the options.

Which of the following is the correct order of visiting nodes for a pre-order traversal?

Click the option that best answers the question.

left, right, root
right, left, root
root, left, right
root, right, left

Identifying the Traversal Pattern

The pattern you're seeing is indicative of a tree traversal algorithm. Specifically, what we're doing can be modeled as a Preorder Traversal.

Why Preorder Traversal?

In preorder traversal, we visit the root first, then traverse the left subtree, and finally the right subtree. This is exactly what we're doing while merging the trees:

Visit the Root: Merge the root nodes of both trees.
Traverse the Left Subtree: Merge the left subtrees of both trees.
Traverse the Right Subtree: Merge the right subtrees of both trees.

Here’s how the Preorder Traversal skeleton code might look in JavaScript:

JAVASCRIPT

1function preOrder(node) {
2  if (!node) return;
3  // Perform some operation on the current node (like merging)
4  preOrder(node.left);  // Traverse the left subtree
5  preOrder(node.right); // Traverse the right subtree
6}

Adaptation for Merging

To adapt this for merging, we would:

Sum the current nodes from both trees and create a new node in the merged tree.
Recursively perform this operation for left and right children.

The skeleton code for Preorder Traversal gives us a good framework to build upon for our merging function.

Traversal is the key

Since we started we'll need to eventually return a merged root, let's go with an pre-order traversal. Pseudocode as follows:

xxxxxxxxxx
 
function preOrder(tree1, tree2) {
  if (tree1 == null) {
    return tree2;
  }
  if (tree2 == null) {
    return tree1;
  }
  return tree1.val + tree2.val;
​
  // Do the above on both of their left children
  preOrder(tree1.left, tree2.left)
​
  // Do the above on both of their right children
  preOrder(tree1.right, tree2.right)
}

Applying this to the problem at hand, doSomeOperation() for us would mean checking the currently investigated node position at both the first and second trees, and deciding what to return.

But what do we need to get back? Here's an operation that might work given our examples:

xxxxxxxxxx
 
if (tree1 == null) {
  return tree2;
}
if (tree2 == null) {
  return tree1;
}
tree1.val = tree1.val + tree2.val
return tree1;

The above code isn't exactly right though-- we're not returning a sum of the two values after checking for null on both, but rather we should be returning a merged node object. To save space, if there are values at both nodes, let's just add them onto the first tree and simply return it.

Let's test your knowledge. Could you figure out the right sequence for this list?

Arrange the following instructions into the correct order to merge two binary trees recursively:

Press the below buttons in the order in which they should occur. Click on them again to un-select.

Options:

If there exists a node:
Use pre-order traversal on the first tree
Return the root of the updated first tree
Continue this process for left subtrees
Check to see if both the tree nodes are null (there exists no node in either tree)
If there exists one node, update the first tree with the value of that node
Continue this process for right subtrees
If there exists two nodes, update the first tree with the sum of the values of both nodes

This needs to be done at every recurrence as we traverse through the trees. However, the traversal needs to be done before we return tree1-- the intuition being that we need to adjust the children of each node before we can give it back. In other words, we should write the merge results on the first tree before presenting it back in our method.

xxxxxxxxxx
 
function mergeTwoBinaryTrees(tree1, tree2) {
  if (tree1 == null) {
    return tree2;
  }
  if (tree2 == null) {
    return tree1;
  }
  tree1.val += tree2.val
​
  tree1.left = mergeTwoBinaryTrees(tree1.left, tree2.left);
  tree1.right = mergeTwoBinaryTrees(tree1.right, tree2.right);
​
  return tree1;
}

Understanding Time Complexity: $O (m + n)$

You've got it spot on! The time complexity of $O (m + n)$ perfectly captures the nature of this problem.

Why $O (m + n)$ ?

Every Node Visited Once: In the process of merging, each node in both trees is visited exactly once.
Single Operation Per Node: At each visit, we perform a constant amount of work (i.e., summing node values and creating a new node).

Considering that there are $m$ nodes in the first tree and $n$ nodes in the second tree, it's quite straightforward to conclude that the overall time complexity is $O (m + n)$ .

The Intuition

Think of it like two separate lists that you need to merge into one. You have to look at each element at least once in both lists to accomplish this. In our case, the lists are just a bit more complex, structured as binary trees. But the fundamental idea remains the same: you have to touch every node at least once.

Try this exercise. Click the correct answer from the options.

What is the time complexity of the recursive tree merger algorithm?

Click the option that best answers the question.

O(1)
O(n!)
O(n log n)
O(n)

One Pager Cheat Sheet

The sum of overlapping nodes is used to create the merged tree, while nodes that do not overlap remain unchanged, within the constraints of O(m+n) time complexity and -1000000000 to 1000000000 for node values.
We can merge trees with just root nodes to gauge how we'd perform this exercise for trees with children.
We can brute force solve a problem by visualizing how a human would do it, and running through examples to find patterns.
The merge rule states that when two nodes overlap, their attributes and properties are combined summarily to form a resultant node.
The merge rule allows any two overlapping nodes to be combined, so it does not have to start from the root nodes of both trees.
We could sum up the node values of two trees, by processing at the root of each one, and then checking for left and right children, according to rule #2.
We scan the tree from left to right and sum up the values we find between each node, returning 4 from the root's left child.
The merge tree function combines the two tree nodes by adding the two elements within them together to get the result.
The algorithm of pre-order traversal is a Depth-First Search which visits the nodes of a tree in the root, left, right order.
We can traverse both trees simultaneously and check their values at each step to create a pattern.
The pre-order traversal technique is the key to returning a merged root.
Checking the node position of the currently investigated element at the first and second trees using doSomeOperation() can determine what to return.
We should merge the two nodes by adding their values onto the first tree, and then simply return it.
The process of merging two binary trees recursively begins with a pre-order traversal of the first tree, checking the nodes of both trees, and then updating the first tree with the sum of their values before continuing with the subtrees.
We should traverse both trees before returning tree1, writing the merge results in the process.
We traverse through both binary trees at once with a time complexity of O(m+n), allowing us to process one node of each tree per iteration.
The time complexity of the recursive tree merger algorithm is O(n), as it only traverses the larger tree, resulting in a worst-case of O(n) nodes.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
    print("Nice job, 2/2 tests passed!")
 
# class Node:
#   def __init__(val):
#     this.val = val
#     this.left = None
#     self.right = None
​
​
def merge_two_binary_trees(tree1, tree2):
    if tree1 is None:
        return tree2
​
    if tree2 is None:
        return tree1
​
    tree1.val += tree2.val
    tree1.left = merge_two_binary_trees(tree1.left, tree2.left)
    tree1.right = merge_two_binary_trees(tree1.right, tree2.right)
    return tree1
​
​
# Node definition
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
​
​
# Regular binary trees
tree1 = Node(4)
tree1.left = Node(1)
tree1.right = Node(3)

Got more time? Let's keep going.

If you had any problems with this tutorial, check out the main forum thread here.

Merging Two Binary Trees

The Problem Statement

The Overlap Rule

The No-Overlap Rule

An Example to Illuminate

Boilerplate Code

Constraints and Expectations

Try to solve this here or in Interactive Mode.

Here's a video of us explaining the solution.

We'll now take you through what you need to know.

Unveiling the Approach: Merging Binary Trees

Step 1: The Simple Case - Merging Root Nodes

The Strategy for Merging Root Nodes

Code Snippet for Merging Root Nodes

The Human Approach to Merging Trees

Running Through Examples to Identify Patterns

Example 1

Example 2

Example 3

Observations

Build your intuition. Fill in the missing part by typing it in.

Try this exercise. Is this statement true or false?

Visualizing the Merging Process

The Steps in the Process

Moving Down to the Left Child Node

A Step-by-Step Look

Result of the Operation

The Recursive Nature

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Let's test your knowledge. Click the correct answer from the options.

Click the option that best answers the question.

Identifying the Traversal Pattern

Why Preorder Traversal?

Adaptation for Merging

Traversal is the key

Let's test your knowledge. Could you figure out the right sequence for this list?

Options:

Understanding Time Complexity: O(m+n)O(m+n)

Why O(m+n)O(m+n)?

The Intuition

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

One Pager Cheat Sheet

This is our final solution.

Got more time? Let's keep going.

Programming Categories

Popular Lessons

Understanding Time Complexity: $O (m + n)$

Why $O (m + n)$ ?