Our brute force solution isn't very optimal, so let's try to make it more efficient. At the very least, notice how we can limit our number of perfect squares to just the ones that are less than our number, since larger ones (in this case, greater than 100) wouldn't make sense. That reduces the time necessary to a degree.

So if we were looking for all the perfect squares that sum up to 12, we wouldn't want to consider 16 or 25-- they're too large for our needs.

To translate this into code, given our previous example, we'd essentially iterate through all numbers smaller than or equal to 100. At each iteration, we'd see if we can find a perfect square that is larger to "fit in" to the "leftover space".

Picture these steps. Start with 28:

Try 16:

Cool, it fits-- let's keep 16. Try 9:

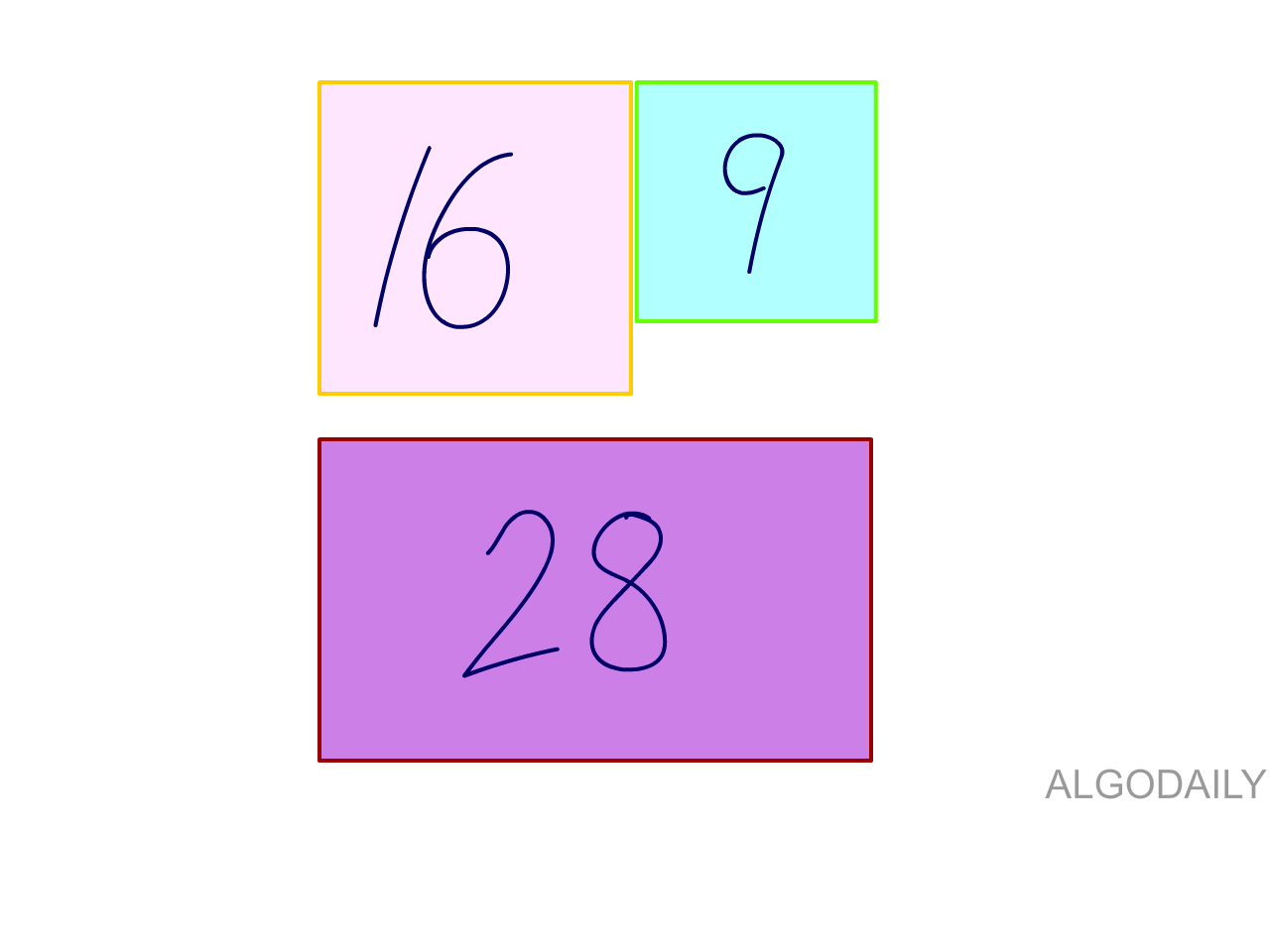
That also fits. What works with 16 and 9?

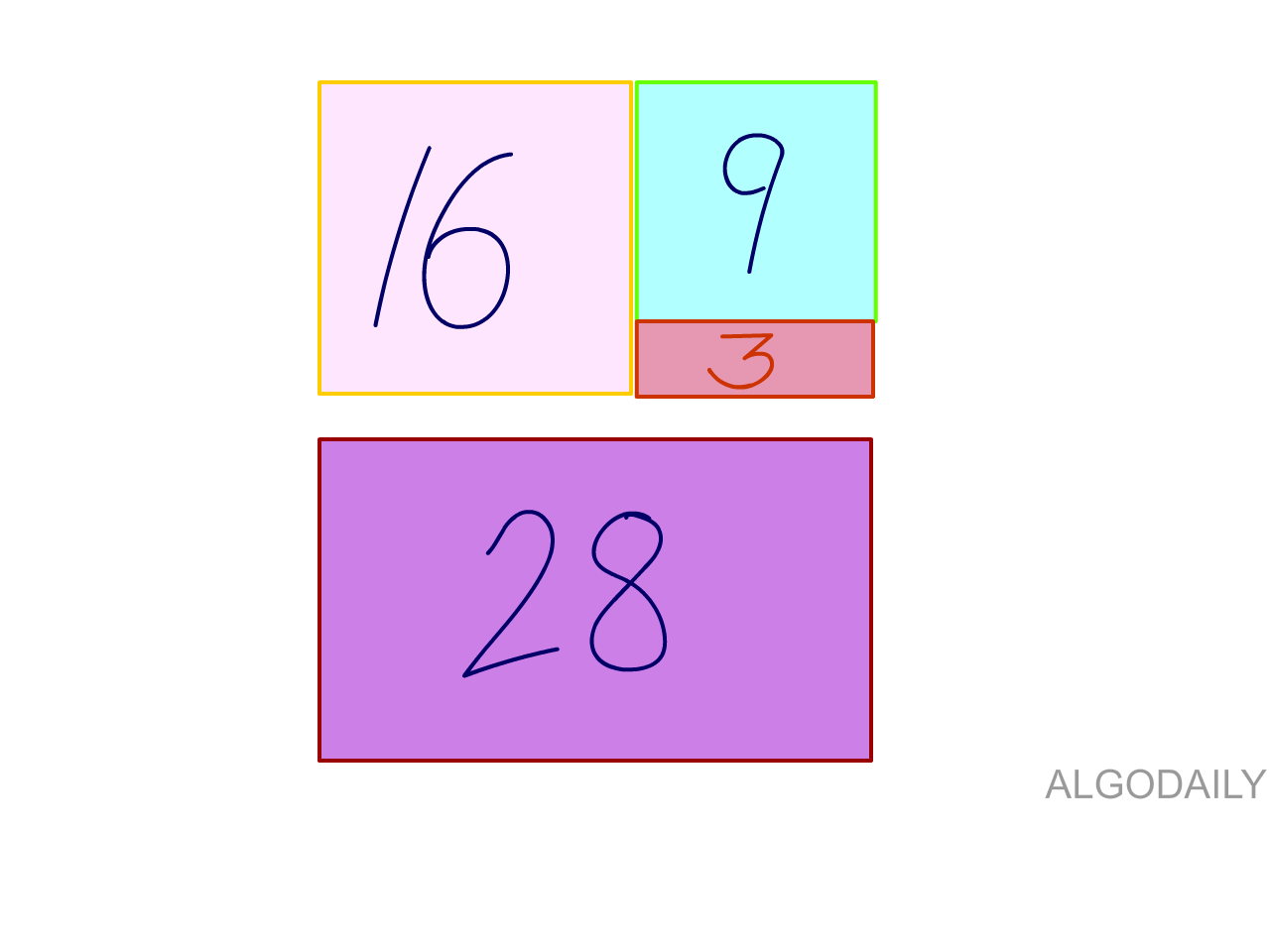
That won't work-- we can only fit 3 but it's not a perfect square. What else fits with 16?

OK, 4 works, and is a perfect square. Notice that it not only matches both conditions (fits and is a perfect square), but we can fit 3 of them in!

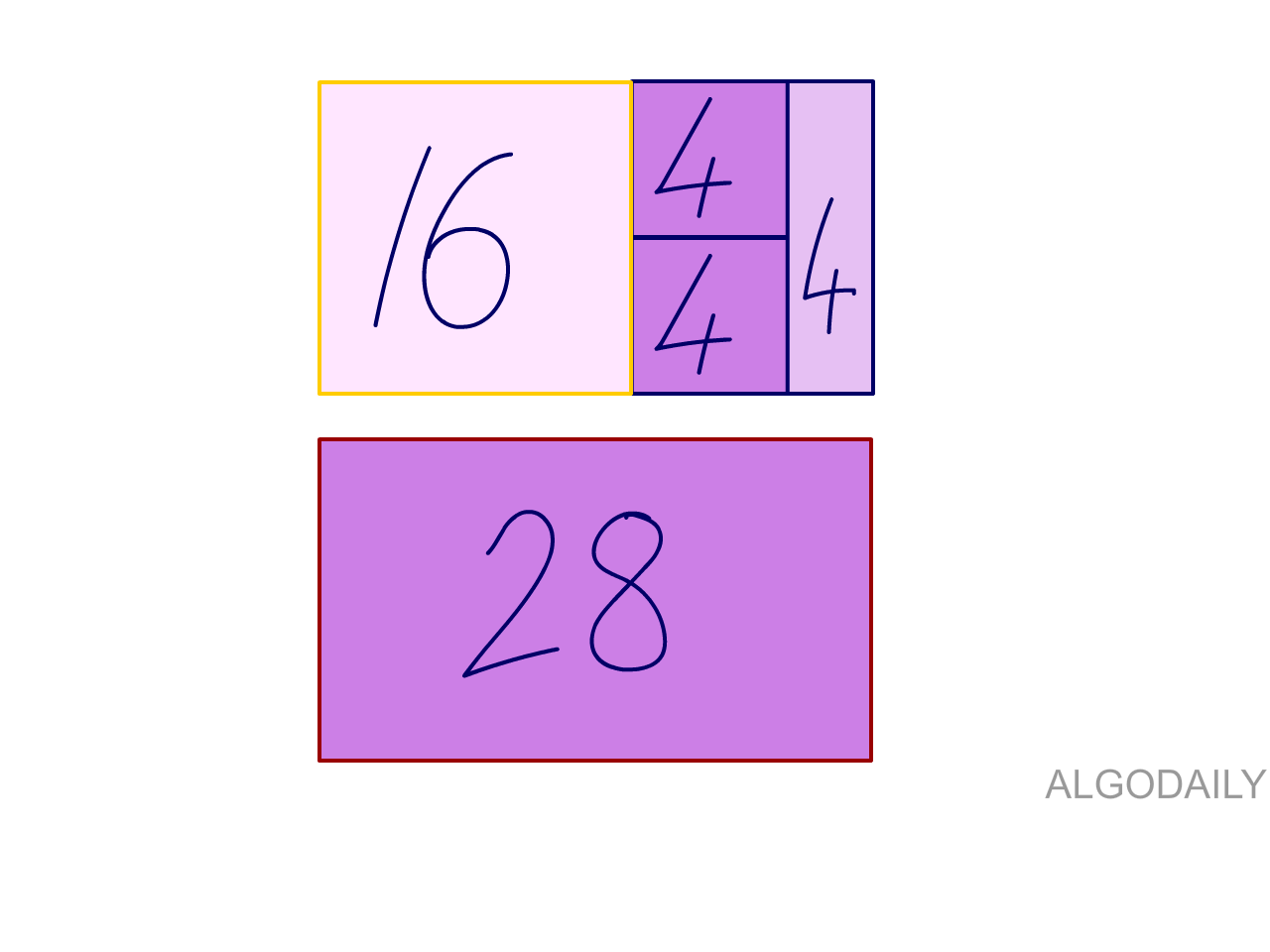
Given that approach, here's the logic translated to code. Read the comments carefully for clarification:

xxxxxxxxxx

function howManySquares(num) {

  if (num <= 3) {

    return num;

  }

​

  result = num;

​

  for (let i = 1; i < num + 1; i++) {

    // get squared number

    temp = i * i;

    if (temp > num) {

      break;

    } else {

      // get whatever is lower:

      // 1 - the current minimum, or

      // 2 - the minimum after considering the next perfect square

      result = Math.min(result, 1 + howManySquares(num - temp));

    }

  }

​

  return result;

}

​

console.log(howManySquares(16));