Good evening! Here's our prompt for today.
Can you justify input text represented by an array of words so it looks pretty when printed and the whitespaces are balanced?

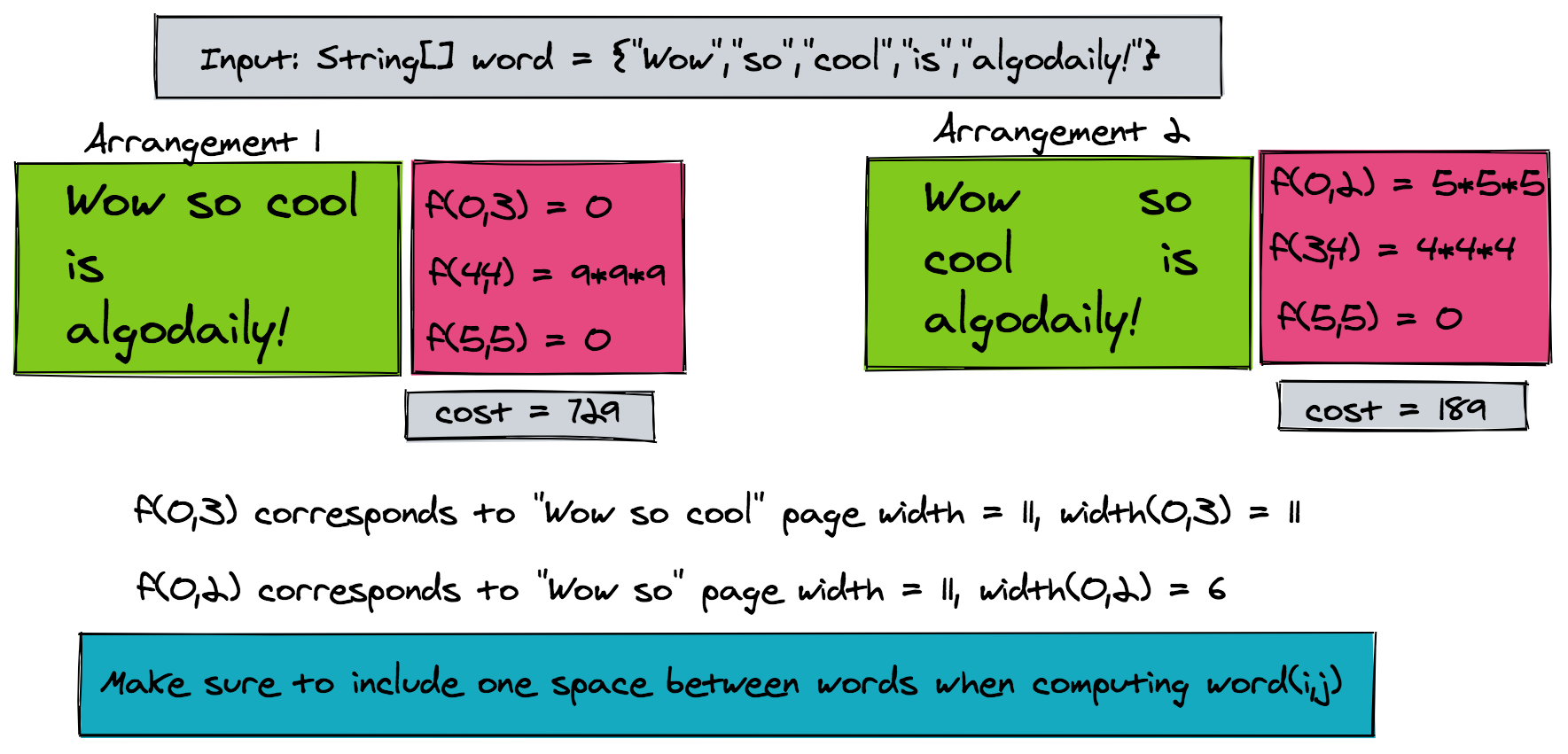
For example, in the above image, we have an input array of ["wow", "so", "cool", "is", "algodaily!"]. This is a list of words we need to properly arrange, with the ideal number of spaces in between, to balance out the layout.
Constraints
- The string can be empty, in which case return an empty string
- The string will consist of only lowercase alphabets
- Expected time complexity :
O(n^2) - Expected space complexity :
O(n)
Text Justification
An obvious solution for text justification is to fit as many words as possible in all the lines. So with ["wow", "so", "cool", "is", "algodaily!"], and an example layout of 10 spaces: we'd place all 3 words: "wow", "so", and "cool", into one single line with no spaces. However, the text would not look pretty if such a naïve scheme is used for justifying text.
A better idea is to evenly distribute spaces on all lines of text for a more aesthetically looking display. This is obvious from the figure shown above, where arrangement 2 is more balanced than arrangement 1.
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxx 'PASSED: `textJustification(wordsLonger)` should return `algodaily \nis awesome\nand you\ncan text\njustify all\ntypes of\ntext and\nwords `'var assert = require('assert');function textJustification(words, maxWidth) { // fill in this method return '';}try { const wordsLonger = [ 'algodaily', 'is', 'awesome', 'and', 'you', 'can', 'text', 'justify', 'all', 'types', 'of', 'text', 'and', 'words', ]; const result = 'algodaily \n' + 'is awesome\n' + 'and you can\n' + 'text \n' +We'll now take you through what you need to know.
How do I use this guide?
Objective Function
For any optimization problem, we have to define the objective function or the fitness function. This is defined as a function that "attempts to maximize profits or minimize losses based on a set of constraints and the relationship between one or more decision variables".
In the case of text justification, the optimization function is dependent upon the number of white spaces being added to each line.
The more the spaces, the poorer "the performance". Hence, we want to minimize the total number of extra spaces that occur in a line.
Based on this idea, the objective function is defined as such: we have a higher value if there are more spaces between words. The goal is to find an arrangement of text that minimizes the objective function.
Let's consider what pieces of information we need. We'll use the following notations in this tutorial. Feel free to refer back to this if you ever get lost.
1n = total number of input words
2L = total number of lines in our solution
3word[i] = word at index i
4f(i,j) = cost function for a line that starts at word[i] and ends at word[j]
5cost = overall cost of the solutionBased on the above notations, let's define width(i, j)-- our objective function-- as:
By using width(i, j) to measure spacing, we have defined the cost function associated with a line that starts with word word[i] and ends at word word[j]. Note that this function is zero for the last line, as we need not add any extra space there.
The figure below shows the example of computing and its corresponding cost for two different arrangements. Our aim is to choose those lines for which the above cost function is a minimum. Hence, we have to find, the indices of the words that lie at the line boundaries, i.e.,:
Armed with the above concepts, we are now ready to define our dynamic programming problem.
Formulation of Dynamic Programming
The problem of text justification can be solved using dynamic programming as it can be divided into sub-problems, each having a recursive sub-structure. We'll define an overall cost function DP[i], associated with each word as given by:
1DP[i] = minimum cost of justifying text that starts with word[i]DP[i] can be defined in terms of the function , that we defined above:
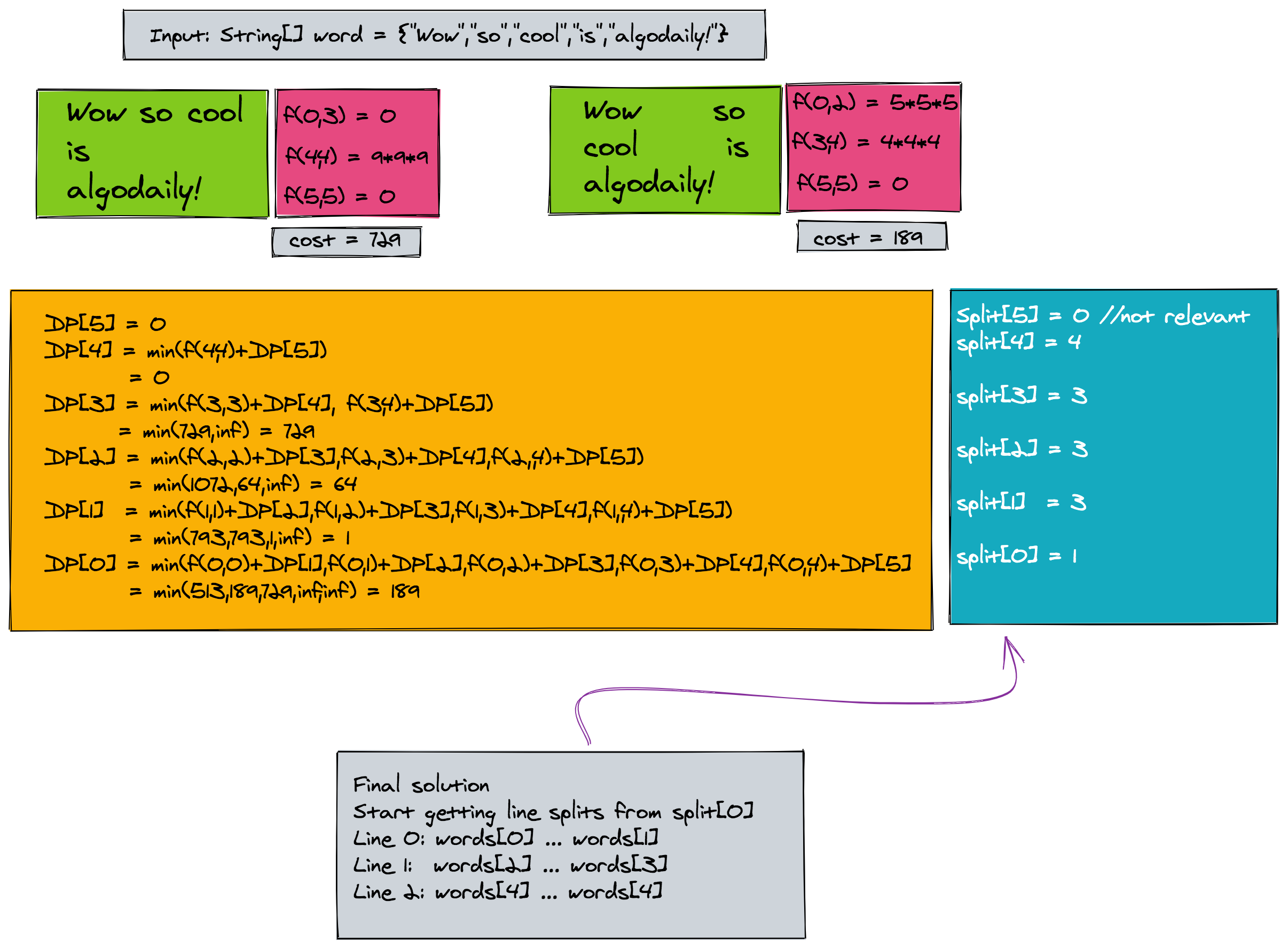
1DP[n] = 0
2DP[i] = min(f(i,j)+DP[j+1]) where min is over j=(i+1)...(n-1)
3 and i=0..(n-1)This gives us a convenient and easy method of finding the word boundaries for each line. Hence we can define split[i], which stores the index of the word that ends the line starting with word[i], in an optimal arrangement.
1split[i] = argmin(f(i,j)+DP[j+1]) where argmin is over j=(i+1)...(n-1)
2 and i=0..(n-1)The final solution's overall cost is DP[0]. Figure below shows DP array for all words of our input word array, with an optimal minimum cost of 189.
Pseudo-code for Computing DP and split
The example from the previous sections shows that we need DP[i] and split[i] for all words in our input array to get the solution for text justification. The pseudo-code for computing DP and split is given below. You can optimize the pseudo-code by cutting down iterations of the for loop in Step 4 by ending the loop if for any j value the misFit is :
xxxxxxxxxxRoutine: getDPInput: index iOutput: DP[i] and split[i]Assumption: DP array initialized to -1 before calling this routine for each indexBase case 1: index exceeds bounds if (i >= n)1. return 0;Base case 2: dp already calculated use memoization (dp[i] != -1)1. return dp[i];Recursive case:1. min = infValue2. minInd = 03. misFit=0 //cost function4. for j=i..(n-1) a. misFit = f(i,j)+getDP(j+1) b. if (misFit < min) { min = misFit minInd = j }5.dp[i] = min;6.split[i] = minInd;7.return dp[i], split[i]Recovering Lines from split
Once split array is filled, we can recover the word boundaries for each line. The following code recovers the lines of text in our final solution. In the code, lineEnd is a list that stores the index of the last word in each line. Its computation is also shown in the last figure.
Once the line endings are determined, we can justify text by inserting the right amount of spaces between words, which is easy to do.
xxxxxxxxxxRoutine: getLinesInput: splitArrayOutput: lineEnd list1. int current = 0;2. do a. lineEnd.add(split[current]) b. current = split[current] c. current = current+1while(current < split.length )3. return lineEndTime and Space Complexity of Text Justification
The recursion tree for DP[0] is shown in the figure below. It shows that O(n) DP values have to be computed, where each requires at the most O(n) computations. This makes an overall time complexity of O(n).

During the solution, we are creating 3 new arrays of the same length of words which is n. So the space complexity will be O(n).
Java Code for Text Justification
The complete Java code for text justification is given below. I am using a large positive integer to represent infinity. The public function solve can be called to determine the split as well as display the justified text. I would encourage you to experiment with the objective function to see how it affects your solution. What would happen if you take square or absolute differences instead of the cube function?
Final Words
Dynamic programming is awesome for text justification! You can look at the greedy solutions and other algorithms too. If you are looking for a quick implementation, then go for a greedy solution as it works for many cases. However, dynamic programming gives you a guarantee that the solution's objective function would be optimized for the solved arrangement of text. Your text would look pretty in the end as the spaces would be evenly distributed on all lines. I hope you enjoy solving this problem as much as I enjoyed writing about it.
xxxxxxxxxx}import java.util.*;class dpTextJustify { int[] dp; //optimal obj func for index i int[] split; //where to split the line int[] len; //length of words int pageWidth; final int infValue = 1000000000; ArrayList < Integer > lineEnd; //main function for text justification public int[] solve(String[] words, int maxWidth) { pageWidth = maxWidth; dp = new int[words.length]; split = new int[words.length]; len = new int[words.length]; for (int i = 0; i < words.length; ++i) { len[i] = words[i].length(); dp[i] = -1; //initialize to -1 } solve(); getLines(); int j = 0; for (int i = 0; i < lineEnd.size(); ++i) { displayLine(words, maxWidth, j, lineEnd.get(i), i == lineEnd.size() - 1); j = lineEnd.get(i) + 1; System.out.print("\n"); } return split;One Pager Cheat Sheet
- We can achieve a more balanced text layout by evenly distributing spaces between all words on each line, while fitting as many words as possible, in
O(n^2)time, usingO(n)space complexity. - Our goal is to minimize the cost of text justification by finding the arrangement of words with the least amount of extra spaces between them.
- Dynamic programming can be used to divide a text justification problem into sub-problems, each with a recursive sub-structure, and an overall cost function can be found using
f(i,j)andDP[i]to determine the optimal word boundary for each line withsplit[i]. - The
DPandsplitarrays can be computed using an optimizedforlooppseudo-codealgorithm. - We can determine the lines of text in our solution by tracking the index of the last word in each line using a
listcalledlineEndand then justifying the text by inserting the right amount of spaces between words. - The time complexity is
O(n$^2$) and the **space complexity** isO(n)` for the dynamic programming solution of the text justification problem.
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx}var assert = require('assert');function textJustification(words, maxWidth) { const res = [[]]; res[0].letters = 0; for (let word of words) { let row = res[res.length - 1]; if (row.length && row.letters + row.length + word.length > maxWidth) { res.push([]); row = res[res.length - 1]; row.letters = 0; } row.push(word); row.letters += word.length; } for (let r = 0; r < res.length; r++) { let row = res[r]; if (row.length === 1 || r === res.length - 1) { res[r] = row.join(' ') + ' '.repeat(maxWidth - row.letters - row.length + 1); continue; } let line = row[0]; let spaces = maxWidth - row.letters; let minSpaces = ' '.repeat(Math.floor(spaces / (row.length - 1))); let addSpace = spaces % (row.length - 1); for (let w = 1; w < row.length; w++) { line += minSpaces + (w <= addSpace ? ' ' : '') + row[w]; } res[r] = line; } return res.join('\n');Alright, well done! Try another walk-through.
If you had any problems with this tutorial, check out the main forum thread here.


