Binary Search Tree

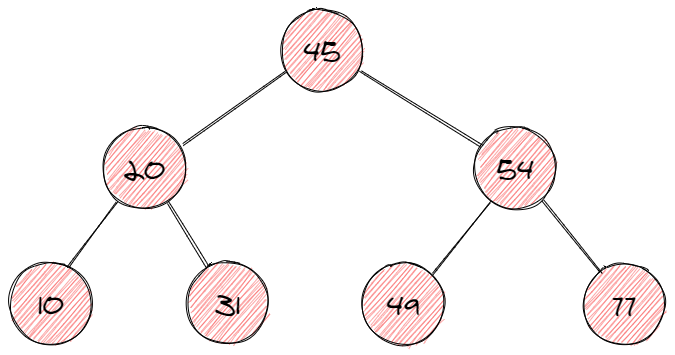
• Quick summary: a kind of binary tree where nodes to the left are smaller, and nodes to the right are larger than the current node.
• Important facts:
  • Nodes of a binary search tree (BST) are ordered in a specific way:
    • All nodes to the left of the current node are smaller (or sometimes smaller or equal) than the current node.
    • All nodes to the right of the current node are larger than the current node.
  • Duplicate nodes are usually not allowed.
• Pros:
  • Balanced BSTs are moderately performant for all operations.
  • Since BST is sorted, reading its nodes in sorted order can be done in O(n), and search for a node closest to a value can be done in O(log(n))
• Cons:
  • Same as trees in general: no constant time operations, performance degradation in unbalanced trees.
• Time complexity (worst case):
  • Access: O(n)
  • Search: O(n)
  • Insertion: O(n)
  • Deletion: O(n)
• Time complexity (average case):
  • Access: O(log(n))
  • Search: O(log(n))
  • Insertion: O(log(n))
  • Deletion: O(log(n))
• See also:
  • An Intro to Binary Trees and Binary Search Trees
  • Interview Problems: Binary Search Trees

xxxxxxxxxx

console.log(bst);

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

class BST {

  constructor(val) {

    this.root = new Node(val);

  }

​

  add(val) {

    let newNode = new Node(val);

​

    function findPosAndInsert(currNode, newNode) {

      if (newNode.val < currNode.val) {

        if (!currNode.left) {

          currNode.left = newNode;

        } else {

          findPosAndInsert(currNode.left, newNode);

        }

      } else {

        if (!currNode.right) {

          currNode.right = newNode;

        } else {

          findPosAndInsert(currNode.right, newNode);

        }

      }

    }