BFS vs. DFS
Understanding Breadth First Search & Depth First Search Search
During the days and weeks before a technical interview, we can apply the 80/20 rule for more efficient preparation. The 80/20 rule, otherwise known as Pareto's Law, stipulates that roughly 80% of your results will come from 20% of your efforts. Once you've gotten more exposure to software engineering interview concepts, you'll find that learning certain techniques will more efficiently improve your ability to solve problems over others.
Breadth First Search (BFS) and Depth First Search (DFS) are two of the most common strategies employed in problems given during an interview. Proficiency in these two algorithms will allow you to solve (in our estimation) at least two-thirds of tree and graph problems that you may encounter in an interview.
Additionally, a surprising number of seemingly unrelated challenges can be mapped as tree or graph problems (see Levenshtein Edit Distance, Split Set to Equal Subsets, and Pick a Sign for just a small sample).
What's a Tree Again?
Let's first revisit trees.
In programming, a tree is a hierarchical data structure with a root node (or vertex-- same thing) and corresponding child nodes. Child nodes can further have their own child nodes. Various types of trees, some which we'll explore shortly, have unique requirements around the number or categorization of its child nodes. In addition, a node with no child is typically called a leaf node.
Let's now look at one with all these types of nodes:
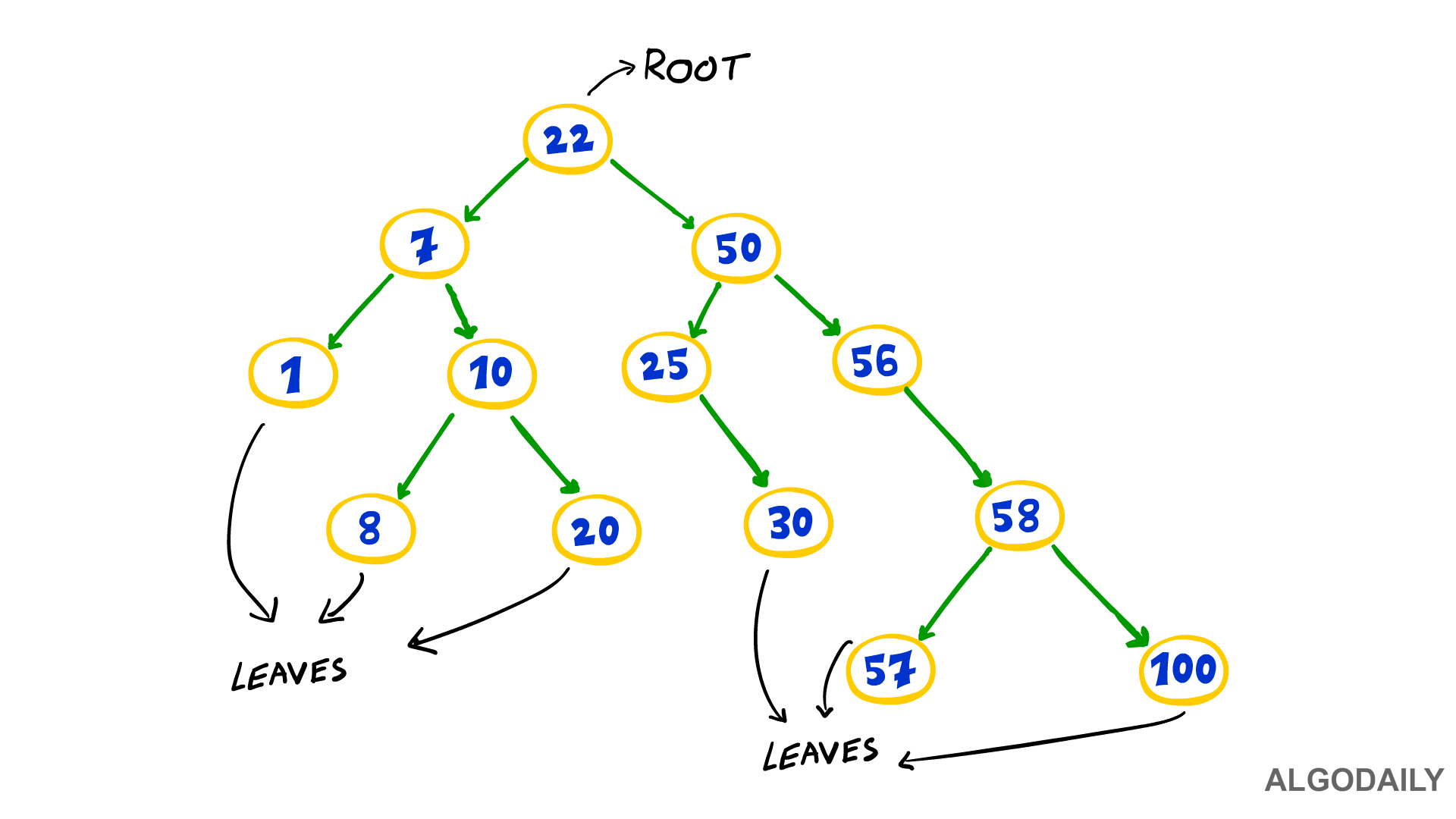
Nodes are connected to each other via edges, also called links or lines. These terms all simply refer to the connection between two vertices.
You may have also heard of traversing a tree. Traversal of a tree refers to the act of visiting, or performing an operation, at each node. Alternatively, searching a tree refers to traversing all the nodes of a tree, where each node is visited only once, to locate a specific node or value.
How Do We Traverse a Tree?
There are two main ways to search a tree: Breadth First Search (BFS) and Depth First Search (DFS). This lesson explains these two search techniques alongside their implementations, and allows for a helpful comparison of the two methods.
To explain the concepts, the following tree will be used as an example:
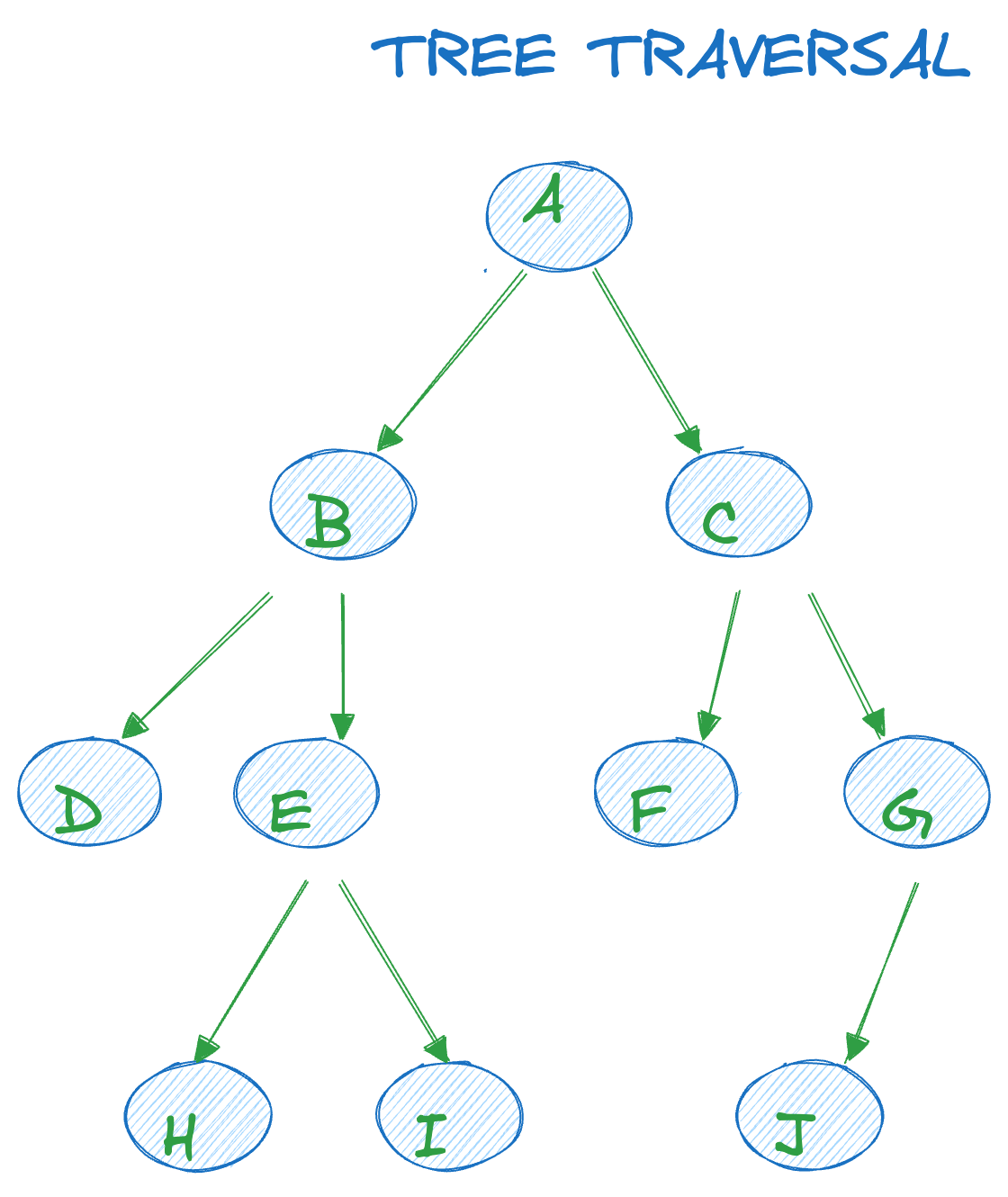
Are you sure you're getting this? Fill in the missing part by typing it in.
What is a node with no children called?
Write the missing line below.
Breadth First Search Theory
In Breadth First Search (BFS), the key is that it is a level-based, or row-based movement. At each level or row, the nodes of a tree are visited/traversed horizontally from left to right or right to left.
The horizontal direction chosen will depend on the problem statement. For instance, a problem that is looking for the sum of all nodes on the right-hand side may necessitate right-to-left traversal. This would allow you to just grab the first node, and immediately move on to the next level, without wasting cycles visiting the others.
In this lesson, we will see how to perform breadth first search from left to right.
Let's take an example. If you look at the previous tree again, the tree has 4 levels:
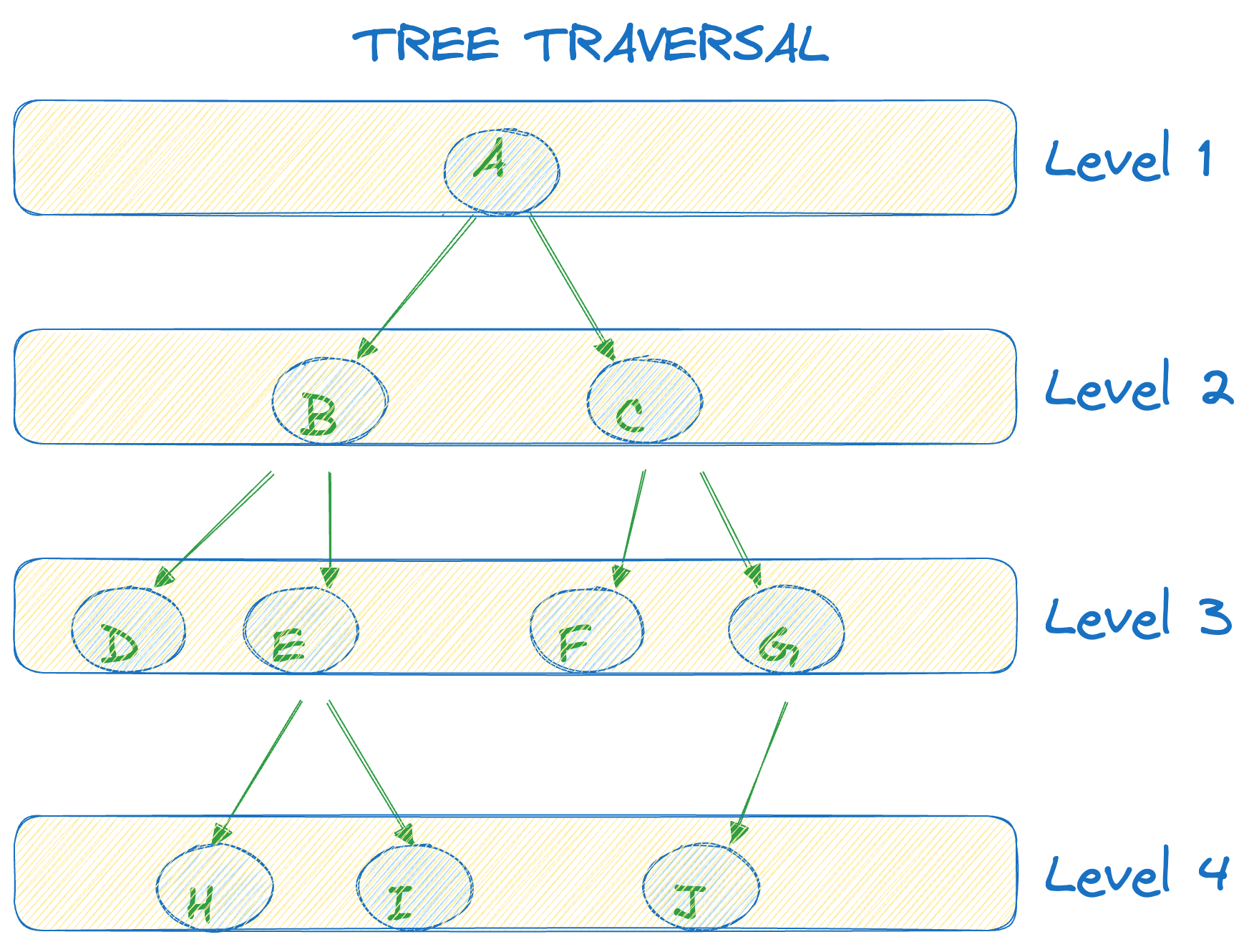
- At level
1, the tree has the root nodeA. - At level
2, it has two nodesBandC. - Similarly, level
3contains nodesD,E,F,G. - Finally, at level
4, nodesH,I,Jare present. If the tree is searched via the breadth first search technique, the nodes would be traversed in the following order:
1A-B-C-D-E-F-G-HLet's discuss implementation, or how we'd actually write the program to conduct BFS. Before jumping into the code, we'll review the steps in plain English. The steps to implement the breadth first search technique to traverse the above tree are as follows:
- Add the node at the root to a
queue. For instance, in the above example, the nodeAwill be added to the queue. - Pop an item from the queue and print/process it.
- This is important-- add all the children of the node popped in step two to the queue. At this point in time, the queue will contain the children of node A:
At this point, we've completed our processing of level 1. We would then repeat steps 2 and 3 for B and C of level 2, and continue until the queue is empty.
1// Step 1
2queue = [A]
3// Step 2
4queue = [B, C]
5// And so on...Here's a visual of the program being run:
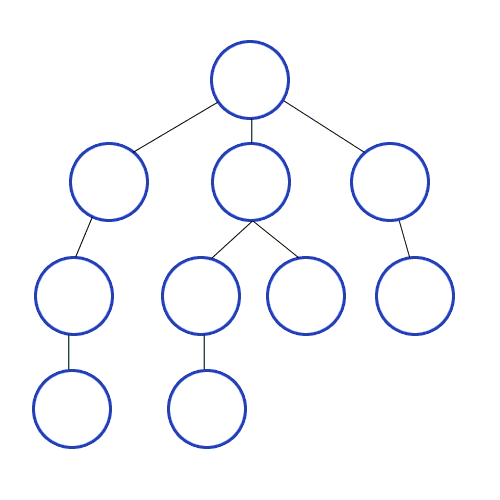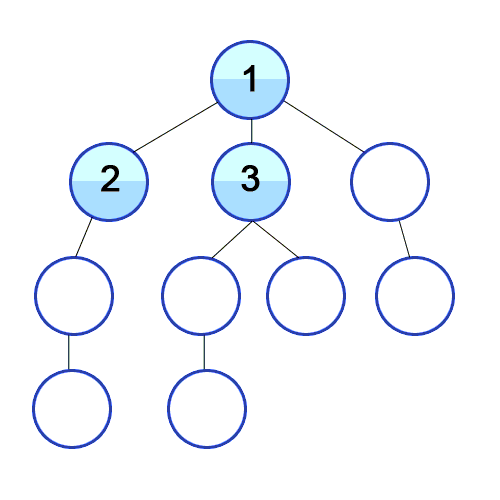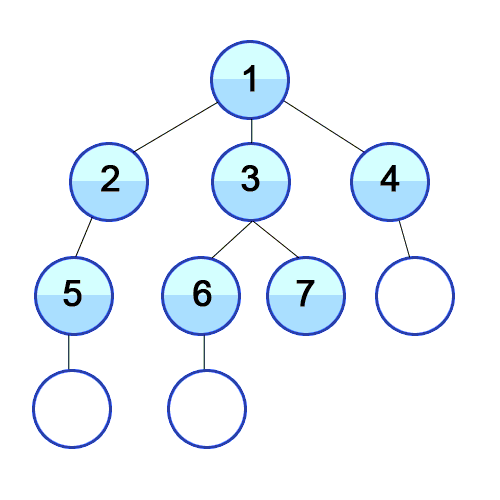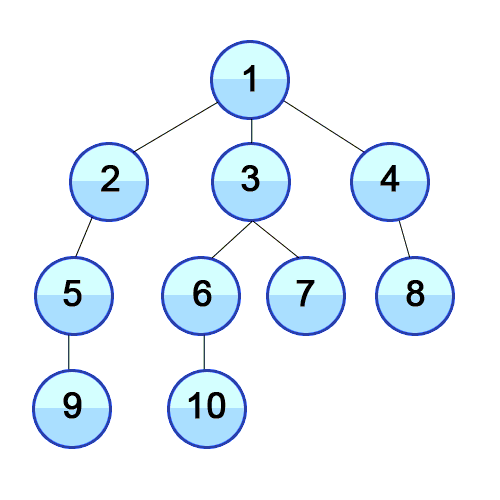
Implementation for BFS
The code implementation for breadth-first search is as follows:
xxxxxxxxxx}import java.util.Iterator;import java.util.LinkedList;public class Main { public static void main(String[] args) { Graph g = new Graph(7); g.AddEdge(1, 2); g.AddEdge(1, 5); g.AddEdge(2, 3); g.AddEdge(2, 5); g.AddEdge(3, 4); g.AddEdge(4, 5); g.AddEdge(4, 6); g.BFS(1); }}class Graph { // Total number of nodes private int NodeNumber; //Adjacent nodes private LinkedList<Integer> AdjacentNodes[]; Graph(int V) {Are you sure you're getting this? Is this statement true or false?
In the Breadth-First Search method, the nodes are traversed horizontally, exclusively and only from left to right.
Press true if you believe the statement is correct, or false otherwise.
In the prior script, we created a class Tree_Node and a method breadth_first_search(). The Tree_Node class contains the value of the root node and the list of child nodes.
The breadth_first_search() method implements steps 1 through 3, as explained in the theory section. You simply have to pass the root node to this method and it will traverse the tree using BFS.
Let's now create a tree with the tree that we saw in the diagram.
1Graph g = new Graph(7);
2
3g.AddEdge(1, 2);
4g.AddEdge(1, 5);
5g.AddEdge(2, 3);
6g.AddEdge(2, 5);
7g.AddEdge(3, 4);
8g.AddEdge(4, 5);
9g.AddEdge(4, 6);In the script above we create a dictionary nodes_dic where each element corresponds to a node of a tree.
The key is the value of the root node, whereas the value of each item in the dictionary is the corresponding list of child nodes. For instance, the first dictionary element contains A as the key, and a list of child nodes B and C as the value.
We will create an object of the root node class, and then initialize it with first item in the dictionary:
1int root_node_value = nodes_dic.keySet().iterator().next();
2List<Integer> root_node_children = nodes_dic.values().iterator().next();
3TreeNode root_node = new TreeNode(root_node_value, root_node_children);Note: The code snippets above assume that the nodes_dic structure and the TreeNode class or struct are defined appropriately in the respective languages. The exact implementation might vary based on the details of those definitions.
Finally, we can simply pass the root node to the breadth_first_search method to traverse the tree.
1depth_first_search(root_node)In the output, you will then see the following expected sequence of nodes:
1visiting 1
2visiting 2
3visiting 5
4visiting 3
5visiting 4
6visiting 6When To Use BFS
Here are a few scenarios and pointers on when to prefer BFS over DFS:
- When you need to find the shortest path between any two nodes in an unweighted graph.
- If you're solving a problem, and know a solution is not far from the root of the tree,
BFSwill likely get you there faster. - If the tree is very deep,
DFSwith heuristics might be faster.
Depth First Search (DFS) Theory
In Depth First Search (DFS), a tree is traversed vertically from top to bottom, or bottom to top. As you might guess from its namesake, we will traverse as deeply as possible, before moving on to a neighbor node. There are three main ways to apply Depth First Search to a tree.
They are as follows:
Preorder Traversal - We start from the root node and search the tree vertically (top to bottom), traversing from left to right. The order of visits is
ROOT-LEFT-RIGHT.In-order Traversal - Start from the leftmost node and move to the right nodes traversing from top to bottom. The order of visits is
LEFT-ROOT-RIGHT.
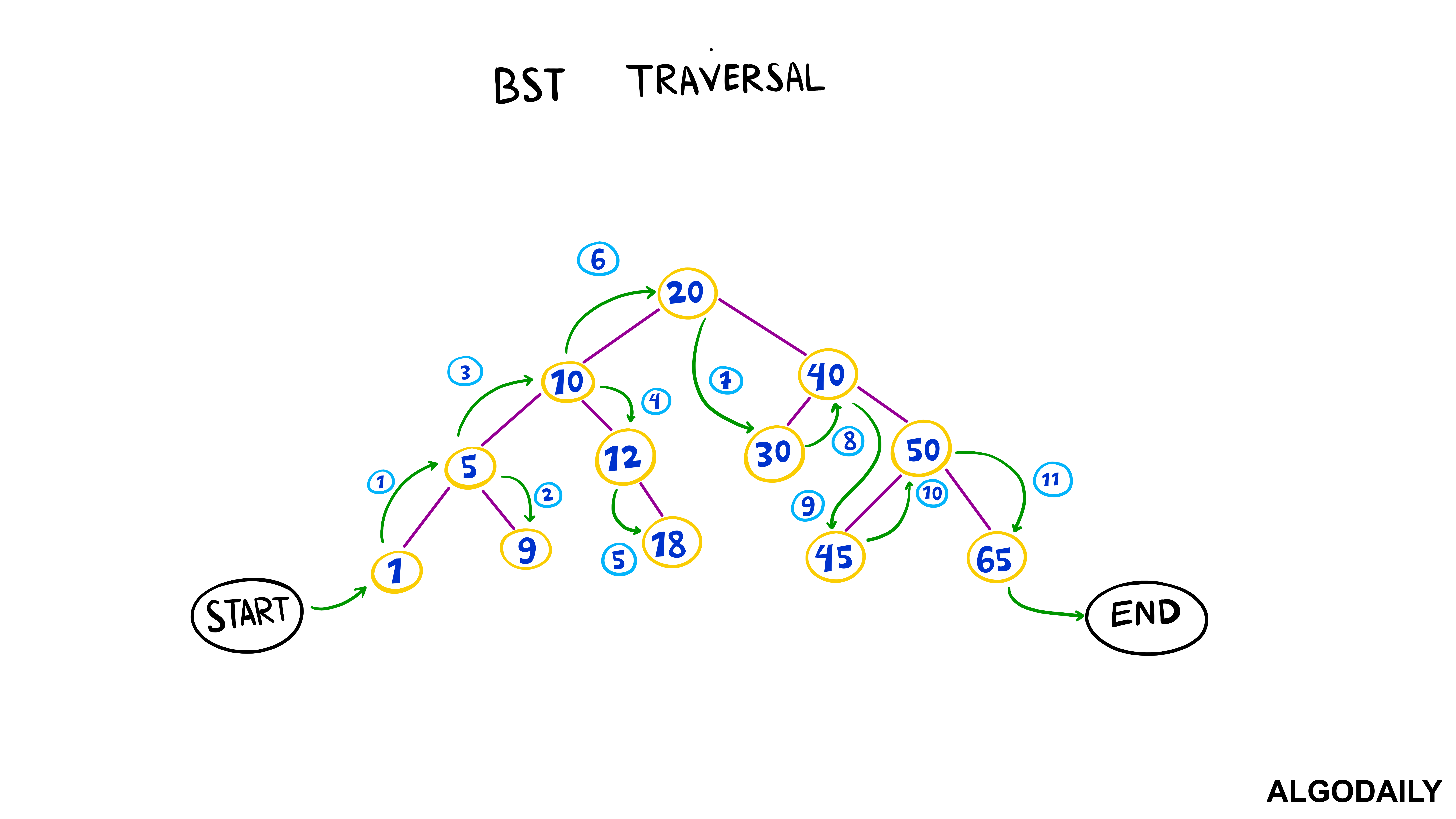
- Post-order Traversal - Start from the leftmost node and move to the right nodes, traversing from bottom to top. The order of visits is
LEFT-RIGHT-ROOT.
Let's focus on Preorder Traversal for now, which is the most common type of depth first search.
If you traverse the example tree in this article using Preorder Traversal, the tree nodes will be traversed in the following order:
1A-B-D-E-H-I-C-F-G-JThe following are the steps required to perform a Preorder Traversal DFS:
- Add the root node to a
stack. For the example tree in this article, the nodeAwill be added to the stack. - Pop the item from the stack and print/process it. The
node Awill be printed. - Add the right child of the node popped in step 2 to the stack and then add the left child to the stack. Because the nodes are traversed from left to right in Preorder Traversal, the node added last in the stack (the left node) will be processed first. In this case, the nodes C and B will be added to the stack, respectively.
- Repeat steps 2 and 3 until the stack is empty.
Implementation for DFS
The sample code for Preorder Traversal DFS is as follows:
1class Graph {
2
3 // Total number of nodes
4 private int NodeNumber;
5
6 //Adjacent nodes
7 private LinkedList<Integer> AdjacentNodes[];
8
9 Graph(int V) {
10 AdjacentNodes = new LinkedList[V];
11 for (int i = 0; i < AdjacentNodes.length; i++) {
12 AdjacentNodes[i] = new LinkedList();
13 }
14 NodeNumber = V;
15 }
16
17 public void AddEdge(int v, int w) {
18 AdjacentNodes[v].add(w);
19 }
20
21 void DFSUtil(int v, boolean visited[]) {
22 visited[v] = true;
23 System.out.print("visiting "+ v + " ");
24
25 Iterator<Integer> i = AdjacentNodes[v].listIterator();
26 while (i.hasNext()) {
27 int n = i.next();
28 if (!visited[n]) {
29 DFSUtil(n, visited);
30 }
31 }
32 }
33
34 public void DFS() {
35 boolean visited[] = new boolean[NodeNumber];
36 for (int i = 0; i < NodeNumber; ++i) {
37 if (visited[i] == false) {
38 DFSUtil(i, visited);
39 }
40 }
41 }
42}The depth_first_search() method in the script above performs Preorder Traversal BFS. Let's create nodes for the example tree and test the working of depth_first_search() method.
xxxxxxxxxx}import java.util.Iterator;import java.util.LinkedList;import java.util.List;public class Main { public static void main(String[] args) { Graph g = new Graph(7); g.AddEdge(1, 2); g.AddEdge(1, 5); g.AddEdge(2, 3); g.AddEdge(2, 5); g.AddEdge(3, 4); g.AddEdge(4, 5); g.AddEdge(4, 6); g.DFS(); }}class Graph { // Total number of nodes private int NodeNumber; //Adjacent nodes private LinkedList<Integer> AdjacentNodes[];Try this exercise. Fill in the missing part by typing it in.
Say we are performing a depth-first search. We start from the leftmost node and move to the right nodes traversing from top to bottom, going left-root-right. Which traversal type are we using?
Write the missing line below.
And here is the final expected output:
1visiting 1
2visiting 2
3visiting 3
4visiting 4
5visiting 5
6visiting 6When To Use DFS
A few pointers on preferring DFS:
- If there's a large branching factor (wide) but limited depth.
DFSis more space-efficient than BFS.- If the tree is very wide,
BFSwill likely be incredibly memory inefficient, soDFScould be better. - If you need to detect a cycle.
Are you sure you're getting this? Click the correct answer from the options.
If we want to find the shortest path between any two nodes in an unweighted graph, which search should we use?
Click the option that best answers the question.
- BFS
- DFS
One Pager Cheat Sheet
- Proficiency in
Breadth First Search(BFS) andDepth First Search(DFS) can greatly improve your ability to solve tree andgraphproblems found in software engineering interviews, and many seemingly unrelated challenges can be mapped astreeorgraphproblems. - A
treeis a hierarchicaldata structurewith a root node and child nodes that can further have their own child nodes connected viaedges, and nodes with no children are calledleafnodes. - We can search a tree using two main techniques:
Breadth First SearchandDepth First Searchwhich have different implementations and benefits. - A tree node without any
descendantsorsubtreeis called a leaf node orterminal node. - Breadth First Search (BFS) is a level-based traversal of a tree's nodes, typically from left to right, allowing for efficient traversal of the right-hand side of the tree.
- We can implement breadth first search to traverse a tree by adding nodes to a
queue, popping items from the queue, printing or processing them, then adding their children to the queue, and repeating until the queue is empty. - The
breadth-first searchalgorithm is implemented in code as shown. - Breadth-First Search (BFS) explores
neighbor nodesbeforedeeper nodesby navigating eachlayerof nodes and their neighbors in any order. - We created a
Tree_Nodeclass and a methodbreadth_first_search(), which takes the root node as input and traverses the tree using BFS. - We create a
dictionarywith keys and values corresponding to a tree's nodes, and use it to initialize aTree_Nodeobject whosevalueis the key of the first element and whosechildrenare its corresponding values. - We can traverse the tree using the
breadth_first_searchmethod by passing in the root node. - You will see the expected sequence
A, B, C, D, E, F, G, H, I, Jin the output, followed by visiting the nodes in order1, 2, 5, 3, 4, 6inPython, JavaScript, C# and Java. - It is recommended to use
BFSin order to find the shortest path between two nodes in an unweighted graph, or when a solution is not far removed from the root of the tree, as opposed to usingDFSin deeper trees with heuristics. Depth First Search(DFS) is a technique for traversing a tree that searches as deeply as possible before moving to neighbor nodes, done through three main methods, such as Preorder Traversal.By adding the left node last to the stack, Preorder Traversal DFS processes the left node first.- The sample code in this article provides implementations of the
Depth-First Searchalgorithm forPython,JavaScript,C#, andJava. - The
depth_first_search()method performs a Preorder Traversal BFS and can be tested using the example tree and its nodes. - We are using In-Order Traversal to traverse the nodes using
left-root-rightlogic in both Breadth-First Search (BFS) and Depth-First Search (DFS) algorithms. - The code outputted a matrix based on DFS algorithm and subsequently, followed a path visiting the elements in order from
1to6. - When the tree is wide but with limited depth and when the need to detect a cycle arises,
DFSis usually a better choice thanBFSin terms of memory efficiency. - BFS is the ideal algorithm for finding the shortest path between any two nodes in an unweighted graph, as it searches level by level and is therefore guaranteed to find the shortest path.

