Home > Data Structures and Algorithms 🚀 > Climb Some Trees > Huffman Coding Algorithm in Data Compression

The Huffman Coding Compression Algorithm

Let's take a deep dive into the Huffman Coding Compression Algorithm and learn how to implement it step by step in various programming languages.

Introduction

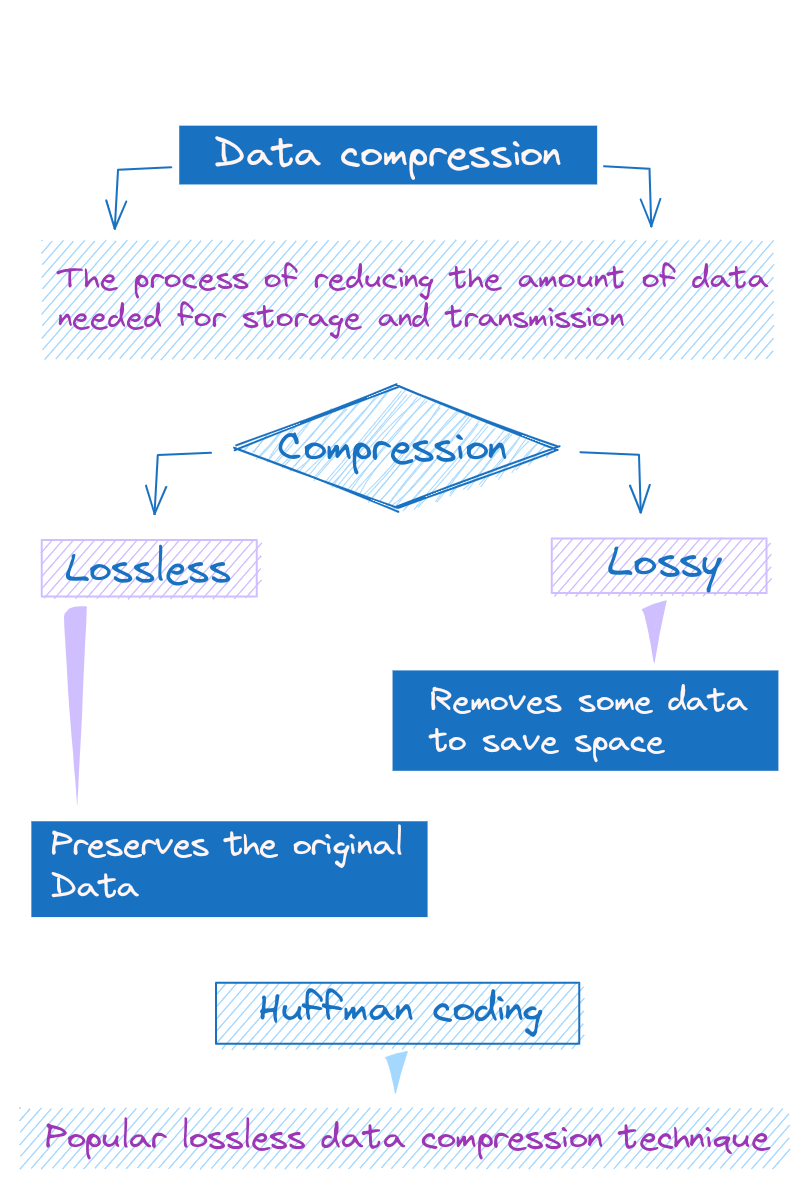
Overview of Data Compression and Its Benefits

Data compression is like packing your suitcase; it's all about fitting a large amount of data into a smaller space. This can save storage space and reduce transmission time when sending files over the internet.

Lossless vs. Lossy Compression

There are two types of compression:

Lossless: Preserves the exact original data (like ZIP files).
Lossy: Removes some data to save space, leading to a reduction in quality (like JPEG images).

Huffman Coding: A Lossless Compression Technique

Huffman coding is a popular lossless data compression algorithm. It’s like writing shorthand for your computer, where more frequent characters get shorter representations.

How Huffman Coding Works

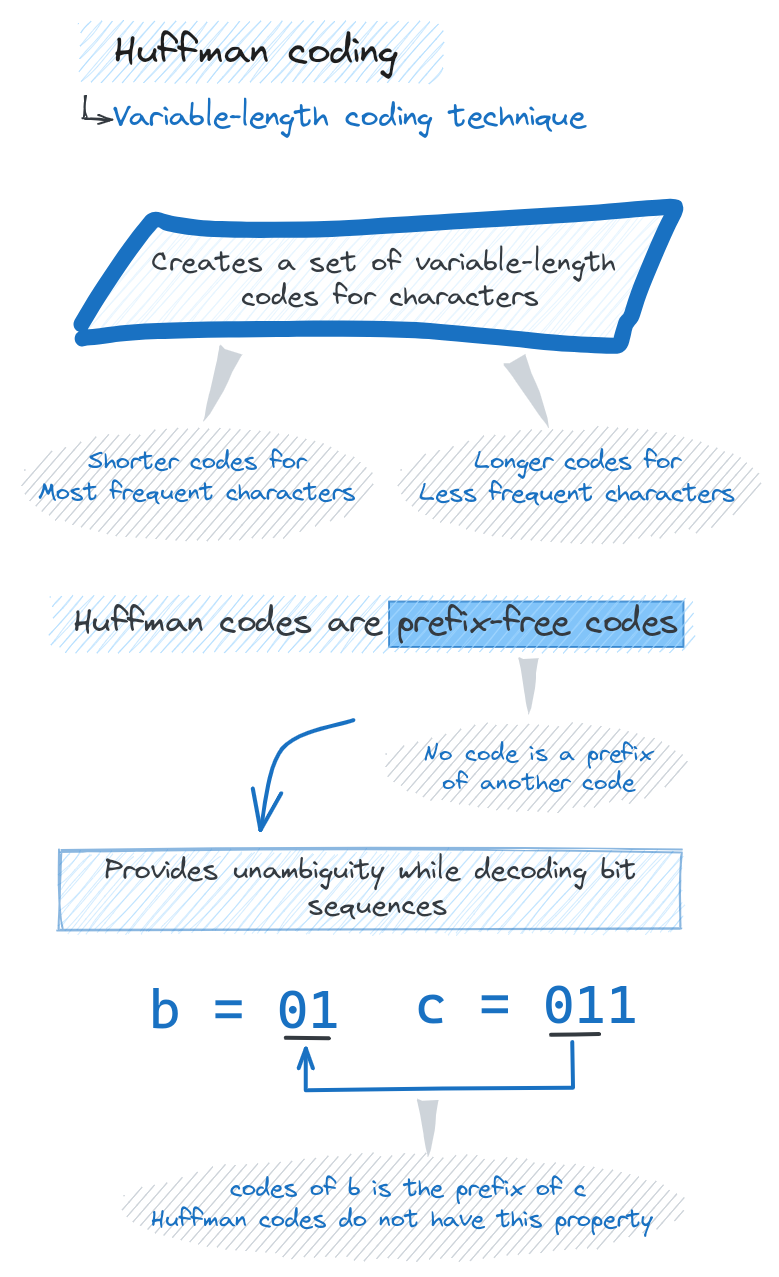
The goal of Huffman coding is to create a set of variable-length codes for characters, with shorter codes for more frequent characters. This allows us to represent data more efficiently and compress the overall size.

Variable-Length Codes

Huffman coding assigns variable-length codes to input characters based on the frequency of those characters. More common characters that appear more often are assigned shorter bit sequences, while less common characters get longer codes.

For example, given the string "hello world", we would construct a frequency table:

SNIPPET

1h - 1
2e - 1 
3l - 3
4o - 2
5w - 1
6r - 1
7d - 1

The character 'l' appears most often, so it would get the shortest code. 'd' appears least often, so it would get the longest code. This encoding allows us to represent common characters very concisely.

Prefix-Free Codes

Huffman codes are constructed in a special way to ensure that no code is a prefix of another code. This prefix-free property allows each bit sequence to be decoded unambiguously.

For example, we would not assign code '01' to 'h' and code '011' to 'e', because '01' is a prefix of '011'. With prefix-free codes, the decoder can follow the bits until a complete code is formed, without ambiguity about when one code ends and another begins.

The prefix-free property is critical for allowing Huffman coding to be lossless and reversible. Given the encoded bit stream, we can unambiguously derive the original data by decoding each complete bit sequence into its matching character.

Building the Huffman Tree

Huffman coding starts by building a binary tree that represents the optimal prefix-free codes based on character frequencies.

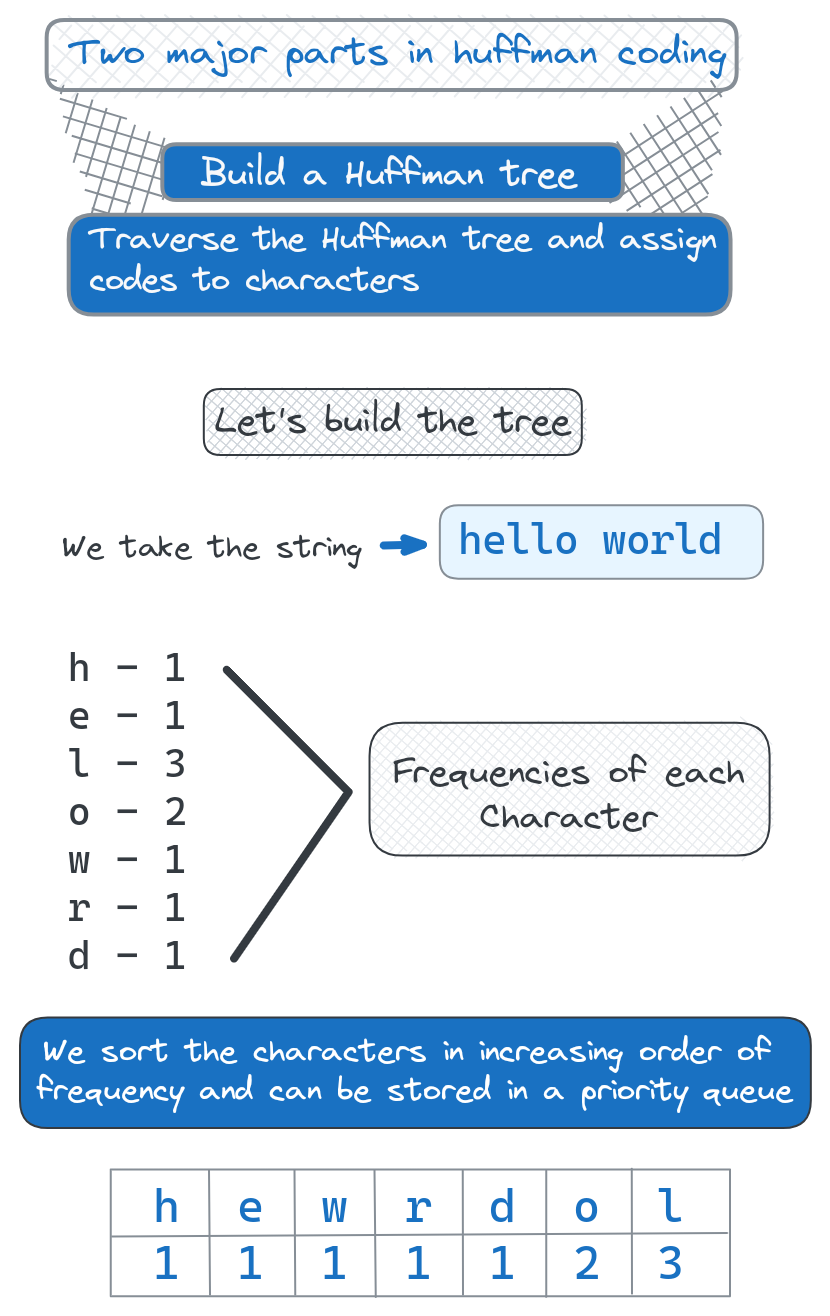
Start with List of Characters and Frequencies

First, we need to know the frequency of each character in the input text. This is tabulated into a list of characters along with their occurrence counts.

For example, given the string "hello world", we would have:

SNIPPET

1h: 1
2e: 1 
3l: 3
4o: 2
5w: 1
6r: 1
7d: 1

Create Leaf Nodes for Each Character

We represent each character as a leaf node in the tree, containing the character and its frequency count.

These leaf nodes form the bottom layer of the tree.

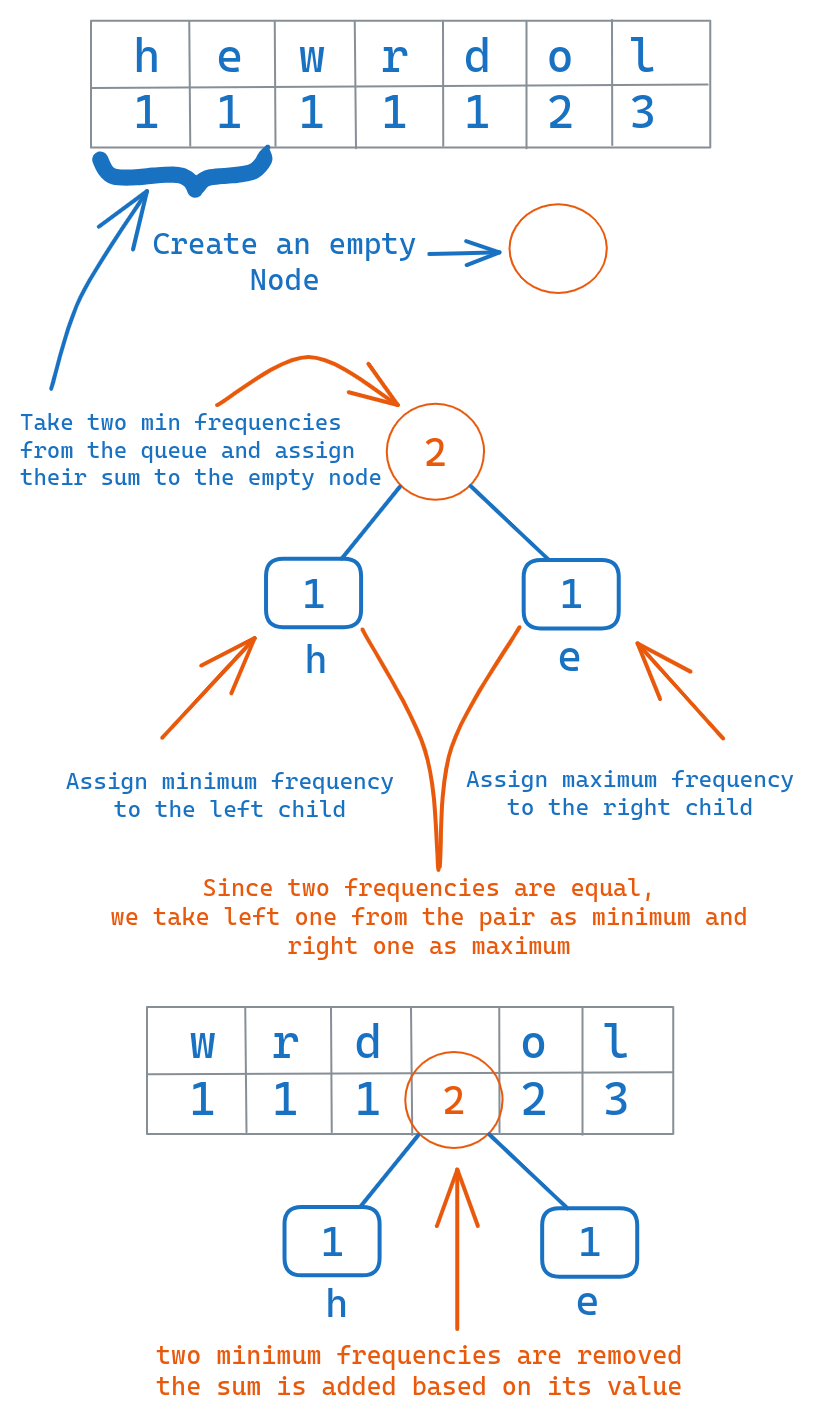
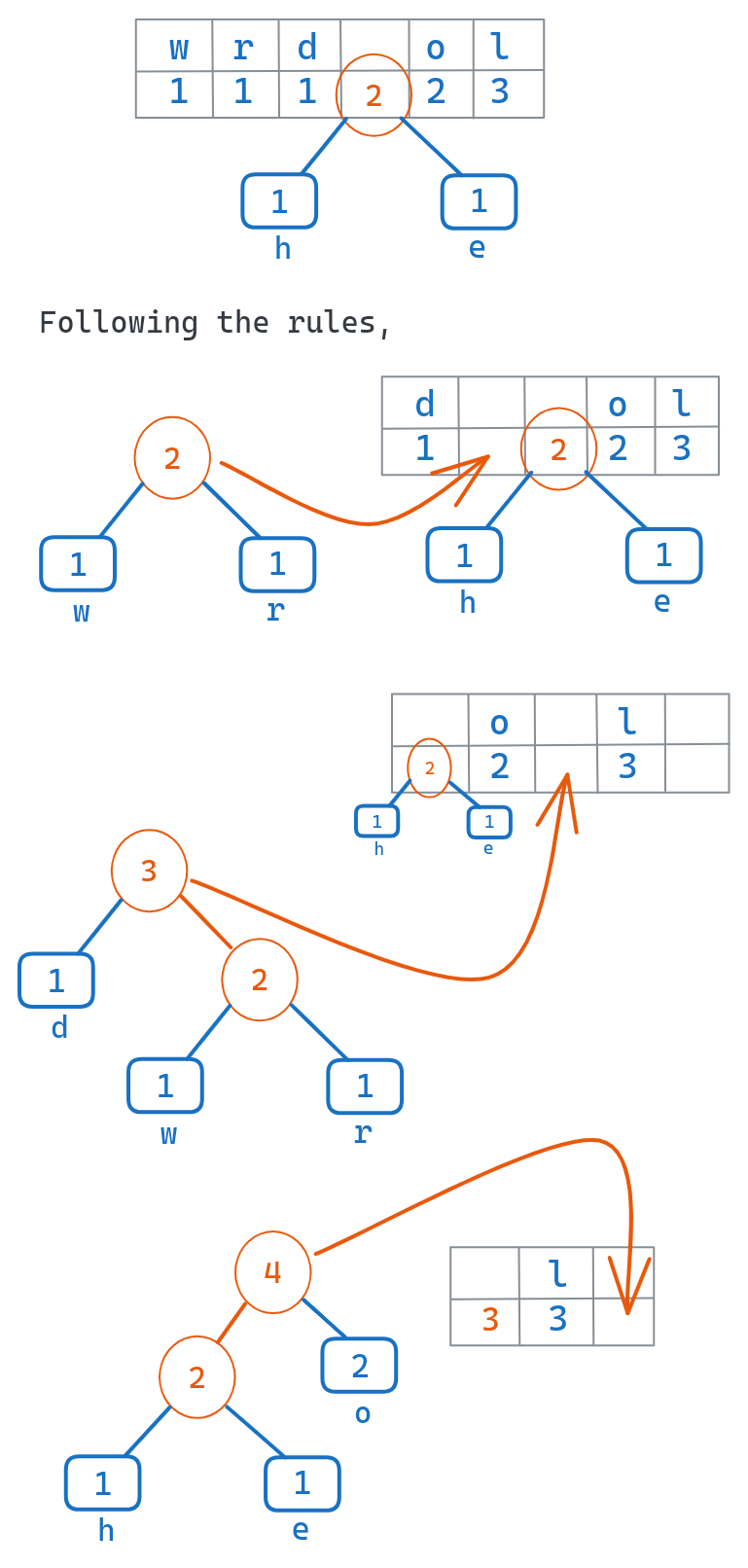
Sort Characters by Frequency

We put the leaf nodes into a priority queue or min-heap, sorted based on the frequencies. The less frequent characters will be at the top, most frequent at the bottom.

This queue structures the nodes in the order that they will be combined.

Iteratively Merge the Two Least Frequent Nodes into a Parent Node

Following the queue order, we repeatedly dequeue the two leaf nodes with the minimum frequencies.

We merge these two nodes into a parent node that has the two nodes as children, and a frequency equal to the sum of the child frequencies.

We enqueue this new parent node back into the priority queue.

Repeat until Only Root Node Remains

We repeat this process of merging the two minimum nodes into a parent, until only one node remains in the queue.

This final node is the root of the entire Huffman tree.

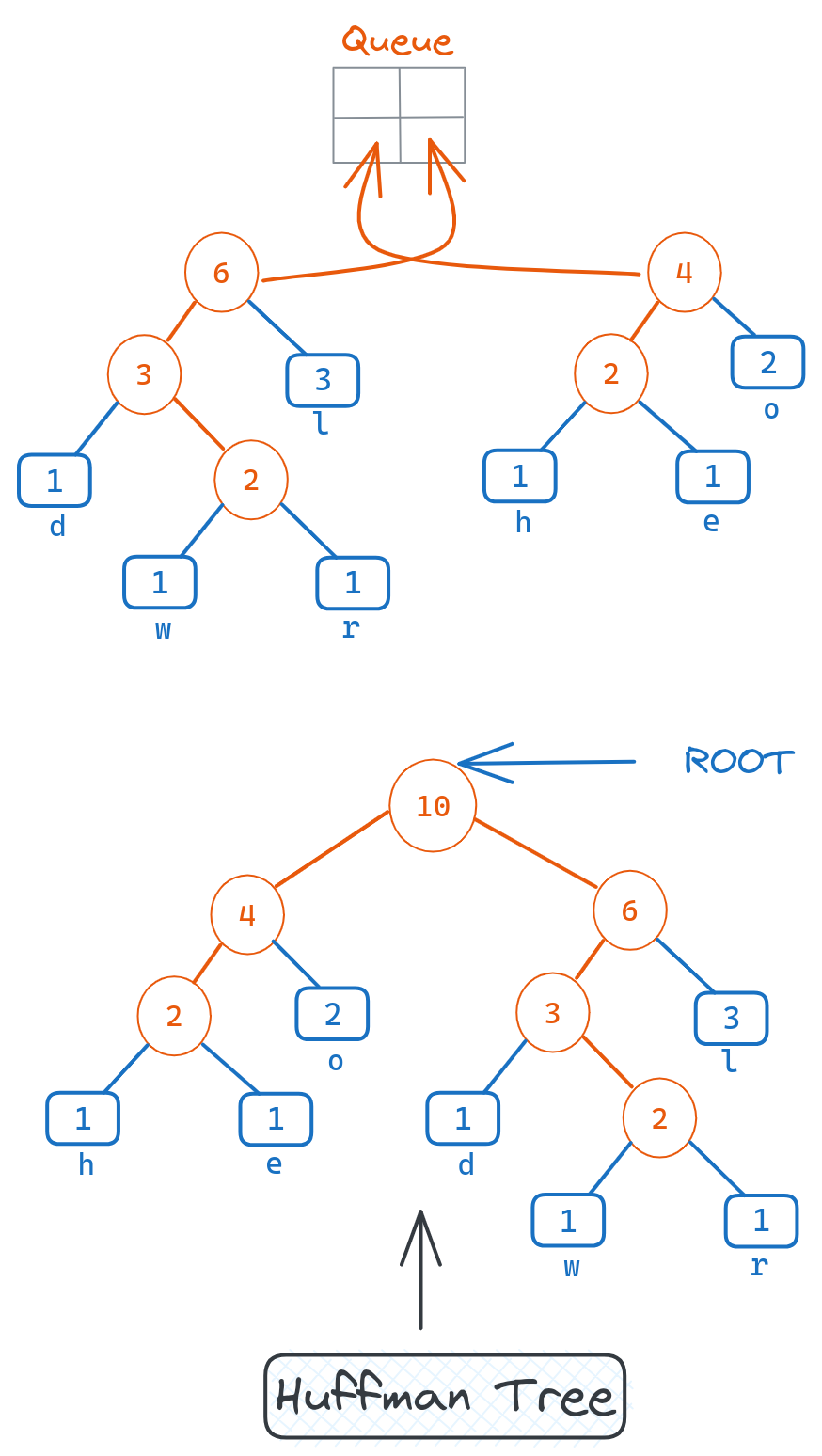
This bottom-up construction ensures that the codes are optimal based on the input frequencies. Frequent characters will be lower in the tree with short path lengths.

Here is example code for building the Huffman tree in various languages:

1// Go code snippet for building Huffman Tree
2
3// ... define Node struct here ...
4
5func buildHuffmanTree(frequencies map[rune]int) *Node {
6    heap := &Heap{}
7    heapTree := &IntHeap{}
8    for char, freq := range frequencies {
9        heap.Push(heapTree, &Node{char: char, freq: freq})
10    }
11    for len(*heapTree) > 1 {
12        left := heap.Pop(heapTree).(*Node)
13        right := heap.Pop(heapTree).(*Node)
14        parent := &Node{freq: left.freq + right.freq}
15        parent.left = left
16        parent.right = right
17        heap.Push(heapTree, parent)
18    }
19    return heap.Pop(heapTree).(*Node)
20}

This code will create a binary tree where the leaf nodes represent the characters, and their path from the root to the leaf represents the code for that character.

xxxxxxxxxx
}
 
package main
​
import (
  "container/heap"
  "fmt"
)
​
type Node struct {
  char       rune
  freq       int
  left, right *Node
}
​
type IntHeap []*Node
​
func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i].freq < h[j].freq }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
​
func (h *IntHeap) Push(x interface{}) {
  *h = append(*h, x.(*Node))
}
​
func (h *IntHeap) Pop() interface{} {
  old := *h
  n := len(old)
  x := old[n-1]
  *h = old[0 : n-1]
  return x

Try this exercise. Fill in the missing part by typing it in.

Huffman coding assigns variable-length codes to input characters based on the _ of those characters

Write the missing line below.

Assigning Codes

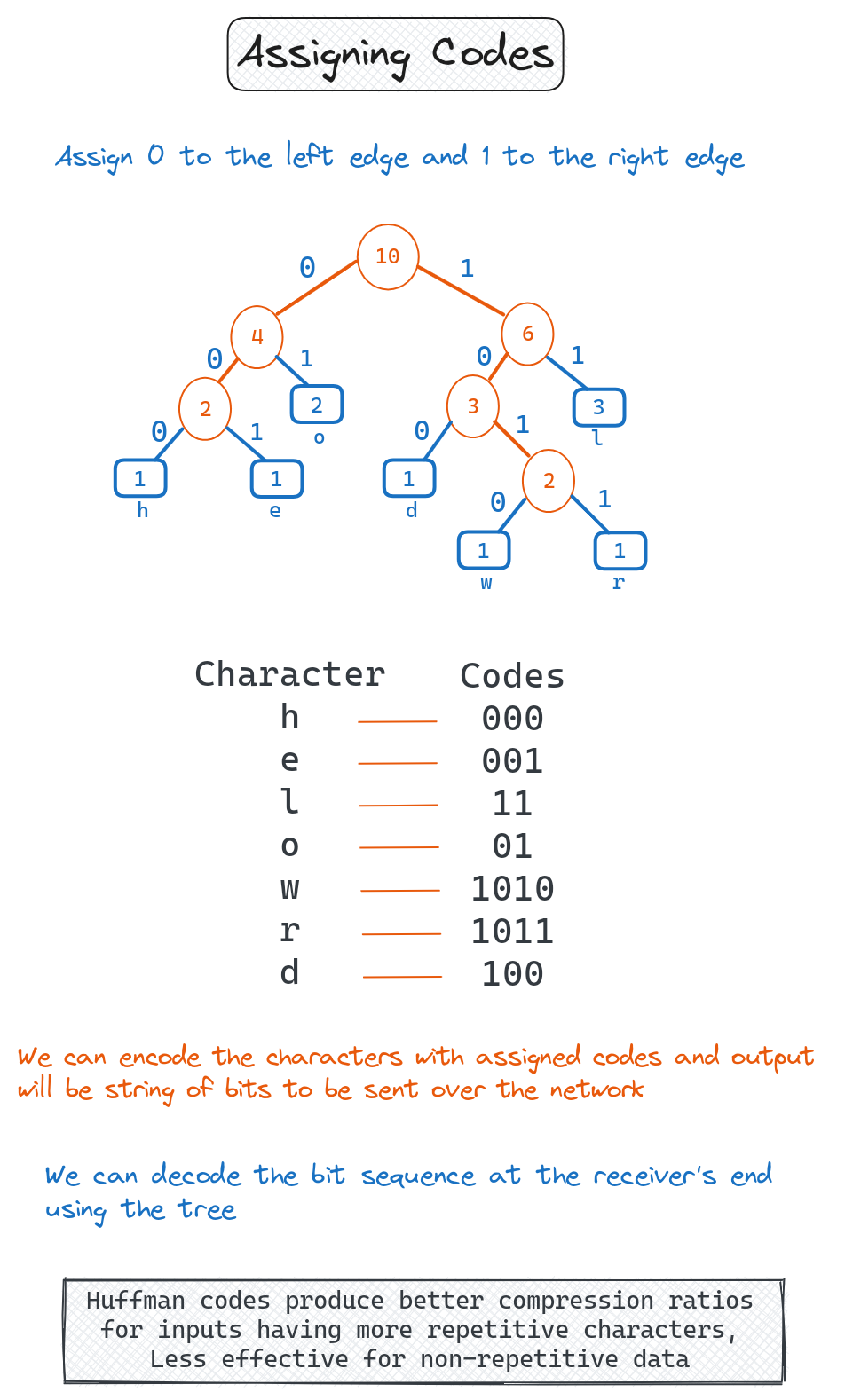
Traverse the Tree to Assign Codes

Recursively traverse the tree, assigning 0 for left branches and 1 for right branches.

More Frequent Characters Get Shorter Codes

The structure of the tree ensures that frequent characters are higher up, resulting in shorter codes.

The code for assigning the codes:

1// Go code for assigning codes
2func assignCodes(node *Node, code string, codes map[rune]string) {
3    if node.char != 0 {
4        codes[node.char] = code
5        return
6    }
7    assignCodes(node.left, code+"0", codes)
8    assignCodes(node.right, code+"1", codes)
9}

xxxxxxxxxx
 
// Go code for assigning codes
package main
​
import "fmt"
​
func assignCodes(node *Node, code string, codes map[rune]string) {
    if node.char != 0 {
        codes[node.char] = code
        return
    }
    assignCodes(node.left, code+"0", codes)
    assignCodes(node.right, code+"1", codes)
}
​
func main() {
    codes := make(map[rune]string)
    // Assume node is a pointer to a Node object representing the root of the Huffman tree
    assignCodes(node, "", codes)
    fmt.Println(codes)
}

Encoding the Input Data

Read Input and Encode Characters with Assigned Codes

Encode each character using the previously assigned codes.

Output the Resulting Bit Sequence

The output will be a string of bits representing the encoded text.

Here's the encoding code:

1// Go code for encoding
2func encode(inputText string, codes map[rune]string) string {
3    var encodedText strings.Builder
4    for _, c := range inputText {
5        encodedText.WriteString(codes[c])
6    }
7    return encodedText.String()
8}

Decoding the Bit Sequence

Decode the Huffman-Encoded Bit Sequence Using the Tree

Use the tree to follow the 0s and 1s back to the original characters.

Here's how you can decode the encoded text:

1// Go code for decoding
2func decode(encodedText string, root *Node) string {
3    node := root
4    var decodedText strings.Builder
5    for _, bit := range encodedText {
6        if bit == '0' {
7            node = node.left
8        } else {
9            node = node.right
10        }
11        if node.char != 0 {
12            decodedText.WriteRune(node.char)
13            node = root
14        }
15    }
16    return decodedText.String()
17}

Algorithm Analysis

Time and Space Complexity Analysis

Time complexity: O(n log n), where n is the number of characters.
Space complexity: O(n), needed for storing the Huffman Tree.

Compression Ratio Analysis

The compression ratio depends on the input data. Texts with more repetitive characters usually get better compression ratios.

Optimizations

There are some techniques we can use to optimize Huffman coding for better performance and compression efficiency.

Using Canonical Code Sets

Canonical Huffman codes use a special property to allow the code table itself to be stored and transmitted more efficiently.

Rather than transmitting the full tree structure to communicate the codes, canonical codes allow the table to be represented as a simple array. The codes are constructed in a way such that the table can be rebuilt based just on the lengths of each code.

This allows for much more compact storage and transmission of the code set needed for decoding. The decoder can rebuild the Huffman tree from the length information rather than requiring the full tree.

Strategies for Tree Rebuilding

In many applications, the input data statistics may change over time. As the frequencies evolve, the optimal Huffman tree also changes.

Adaptive Huffman coding approaches address this by periodically rebuilding the tree to reflect the updated frequencies. This allows the compression to continuously adapt for maximum efficiency.

Some common strategies include:

Rebuilding after a certain number of inputs or time interval
Rebuilding when the compression ratio falls below a threshold
Incrementally updating the tree with new frequencies rather than full rebuilds

The frequency of tree rebuilds involves tradeoffs between compression optimality and computational overhead. More frequent rebuilding provides better compression but requires more computation.

Summary

Huffman coding is a powerful technique for lossless data compression. It's like a personalized shorthand, where the characters you use most often are given the shortest codes.

Through the above examples, you've learned how to:

Build a Huffman Tree
Assign Huffman codes to characters
Encode and decode using Huffman codes

Key applications of Huffman coding include file compression and transmission protocols. Its main limitation is that it is less effective with non-repetitive data.

With this understanding, you are well-equipped to utilize Huffman coding in various computer science and software engineering applications. Happy coding!

One Pager Cheat Sheet

The article provides a guide on the Huffman Coding Compression Algorithm, a lossless data compression technique used to store large amounts of data in smaller spaces, similar to ZIP files, by assigning shorter representations to more frequent characters.
Huffman coding works by creating a set of variable-length codes for characters based on their frequency, employing prefix-free codes to allow for unambiguous decoding.
To build a Huffman tree, start with a list of characters and their frequencies, represent each character as a leaf node with a frequency, sort characters by frequency using a priority queue or min-heap, and then repeatedly merge the two least frequent nodes into a parent node until only one node, the root, remains, which can be achieved in various programming languages like Python, Java, JavaScript, C++, and Go.
Huffman coding assigns variable-length codes to input characters based on the frequency of those characters.
The text provides code in various programming languages (Python, Java, JavaScript, C++, and Go) to recursively traverse a tree, assigning 0 for left branches and 1 for right branches, with the structure designed so that more frequent characters get shorter codes.
This passage describes how to encode input data by encoding each character using previously assigned codes and outputting a bit sequence, using provided encoding code examples in multiple programming languages: Python, Java, JavaScript, C++, and Go.
The provided Python, Java, JavaScript, C++, and Go code snippets illustrate how to decode a Huffman-encoded bit sequence by using a binary tree, traversing left or right based on the bit (0 or 1) and appending the character found at the leaf node to the decoded_text.
The algorithm analysis reveals a time complexity of O(n log n) and a space complexity of O(n) due to the storage of the Huffman Tree, and the compression ratio is dependent on the repetitiveness of characters in the input data.
The use of Canonical Huffman codes enables more efficient storage and transmission of the code table, and adaptive Huffman coding can be utilized for tree rebuilding in dynamic situations where the input data changes over time.
Huffman coding is a method for lossless data compression that assigns the shortest codes to the most frequently used characters, and its uses include file compression and transmission protocols, but it struggles with non-repetitive data.