Building the Huffman Tree

Huffman coding starts by building a binary tree that represents the optimal prefix-free codes based on character frequencies.

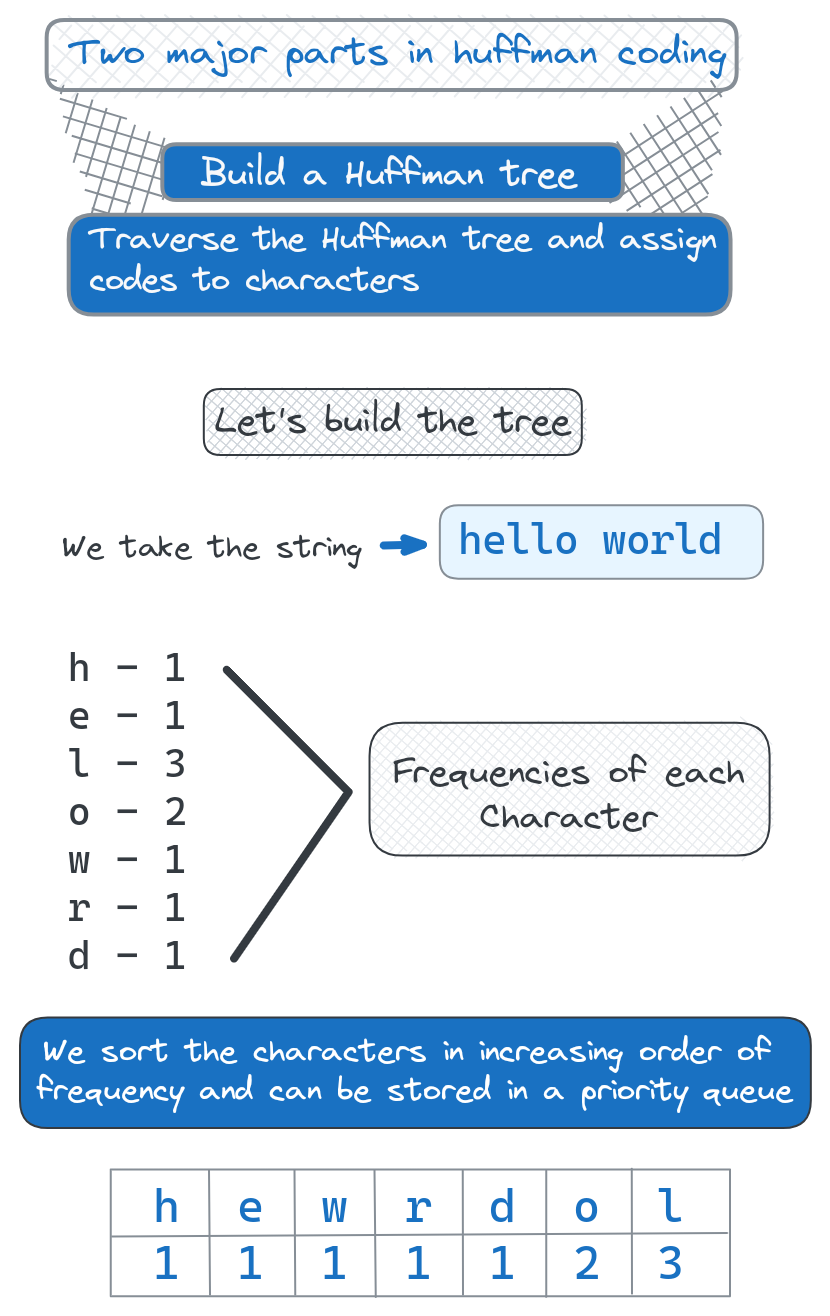
Start with List of Characters and Frequencies

First, we need to know the frequency of each character in the input text. This is tabulated into a list of characters along with their occurrence counts.

For example, given the string "hello world", we would have:

1h: 1
2e: 1 
3l: 3
4o: 2
5w: 1
6r: 1
7d: 1

Create Leaf Nodes for Each Character

We represent each character as a leaf node in the tree, containing the character and its frequency count.

These leaf nodes form the bottom layer of the tree.

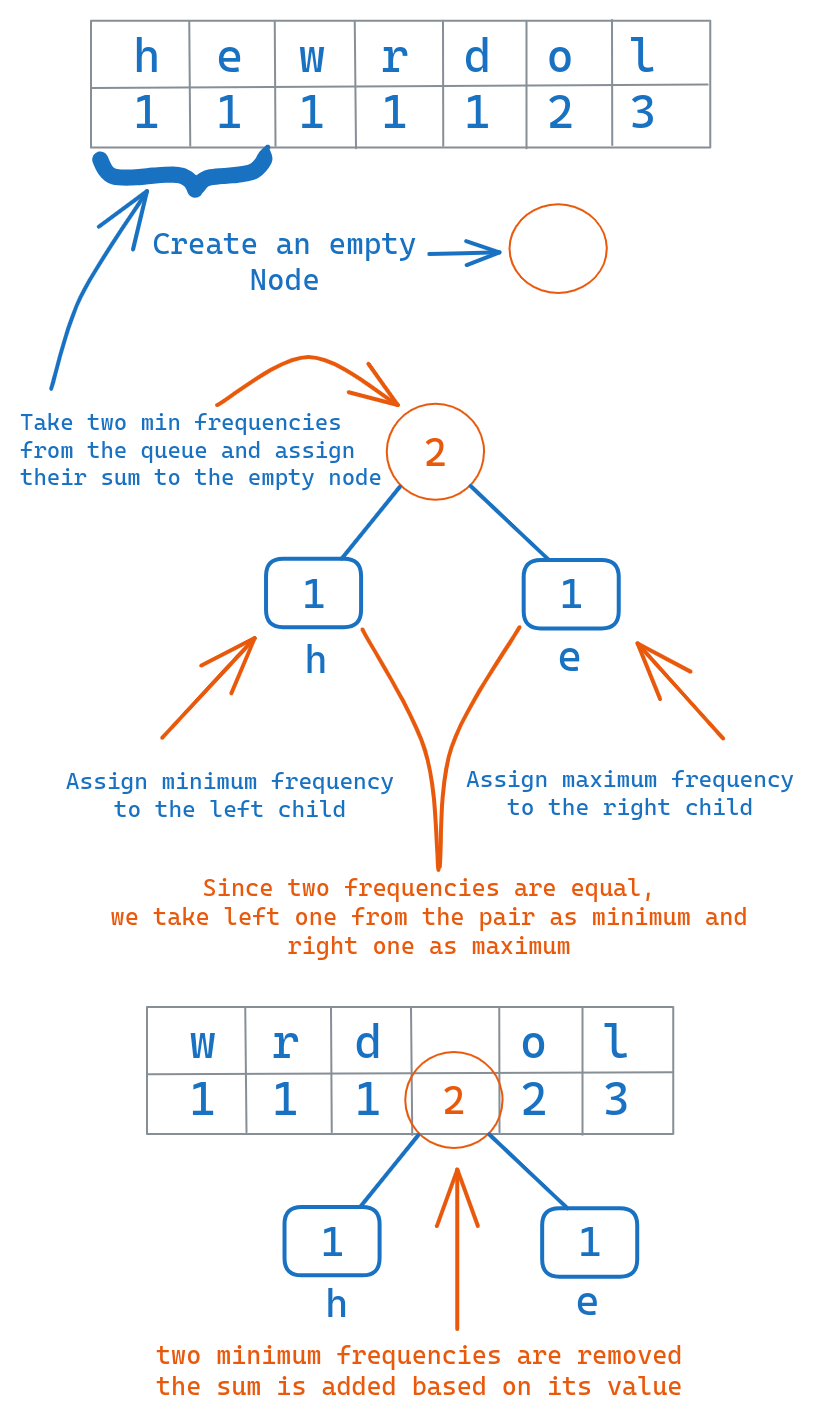
Sort Characters by Frequency

We put the leaf nodes into a priority queue or min-heap, sorted based on the frequencies. The less frequent characters will be at the top, most frequent at the bottom.

This queue structures the nodes in the order that they will be combined.

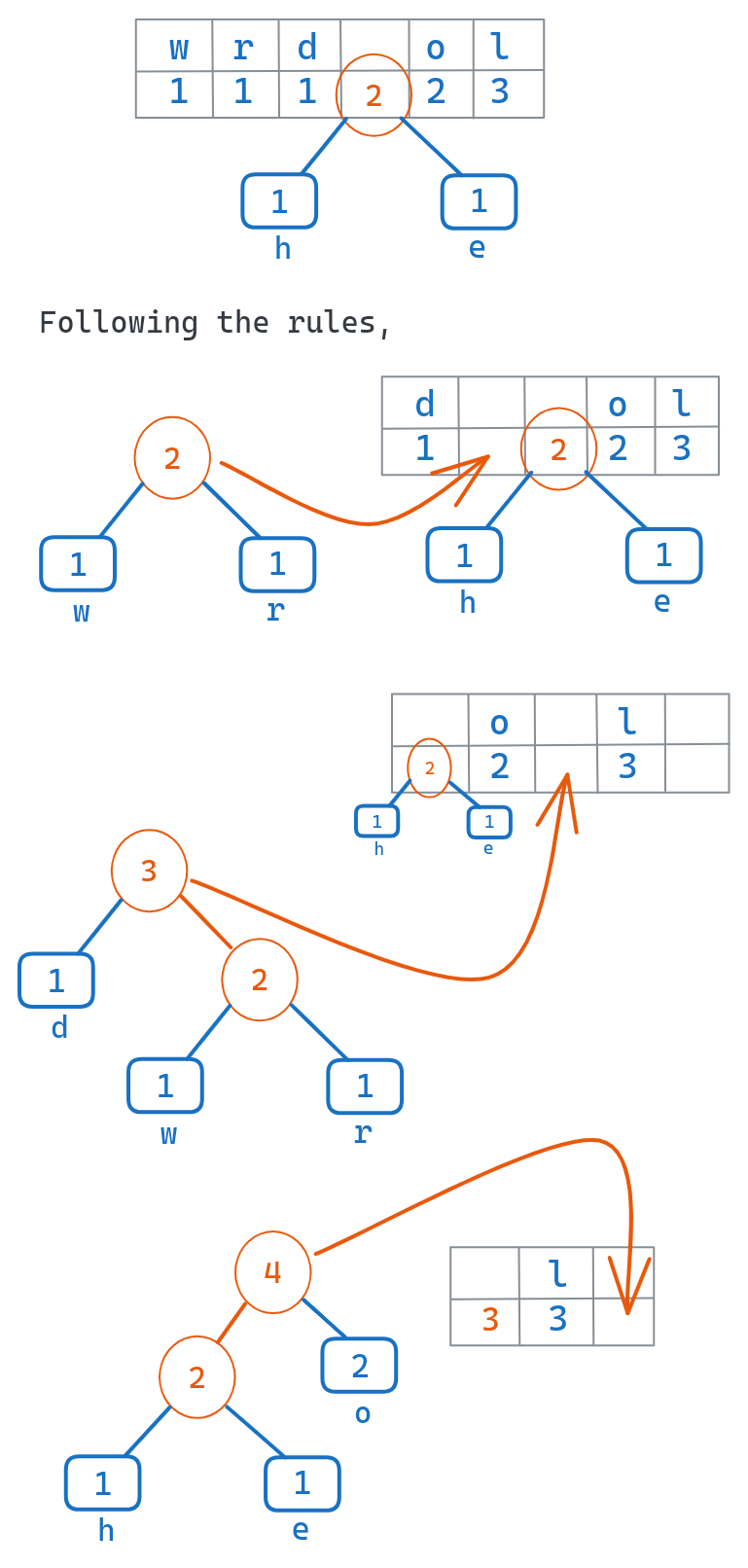
Iteratively Merge the Two Least Frequent Nodes into a Parent Node

Following the queue order, we repeatedly dequeue the two leaf nodes with the minimum frequencies.

We merge these two nodes into a parent node that has the two nodes as children, and a frequency equal to the sum of the child frequencies.

We enqueue this new parent node back into the priority queue.

Repeat until Only Root Node Remains

We repeat this process of merging the two minimum nodes into a parent, until only one node remains in the queue.

This final node is the root of the entire Huffman tree.

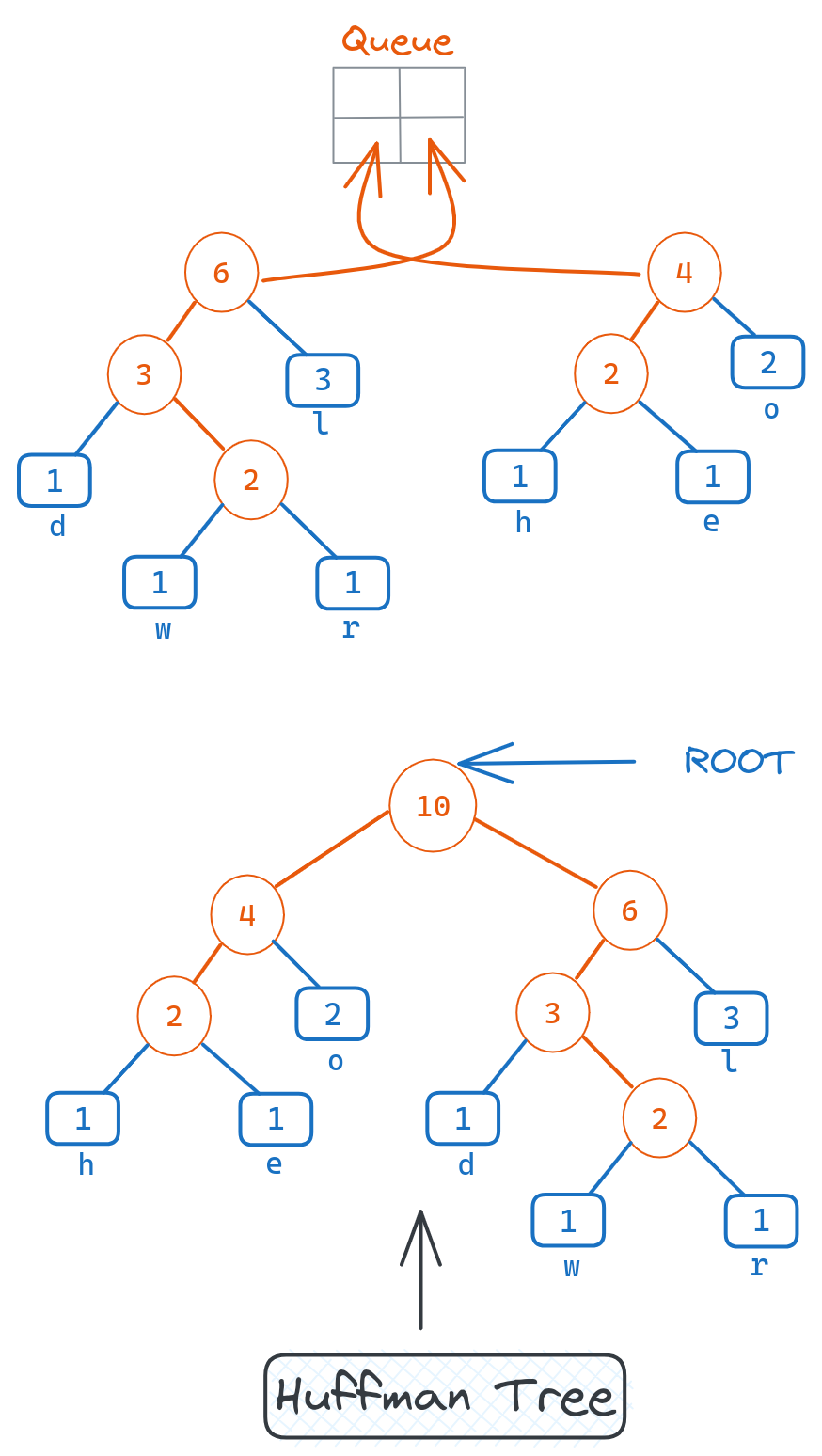
This bottom-up construction ensures that the codes are optimal based on the input frequencies. Frequent characters will be lower in the tree with short path lengths.

Here is example code for building the Huffman tree in various languages:

1// JavaScript code snippet for building Huffman Tree
2
3// ... define Node class here ...
4
5function buildHuffmanTree(frequencies) {
6    let heap = [];
7    for (let char in frequencies) {
8        heap.push(new Node(char, frequencies[char]));
9    }
10    heap.sort((a, b) => a.freq - b.freq);
11    while (heap.length > 1) {
12        let left = heap.shift();
13        let right = heap.shift();
14        let parent = new Node(null, left.freq + right.freq);
15        parent.left = left;
16        parent.right = right;
17        heap.push(parent);
18        heap.sort((a, b) => a.freq - b.freq);
19    }
20    return heap[0];
21}

This code will create a binary tree where the leaf nodes represent the characters, and their path from the root to the leaf represents the code for that character.

xxxxxxxxxx

class Node {

    constructor(char, freq) {

        this.char = char;

        this.freq = freq;

        this.left = this.right = null;

    }

}

​

function buildHuffmanTree(frequencies) {

    let heap = [];

    for (let char in frequencies) {

        heap.push(new Node(char, frequencies[char]));

    }

    heap.sort((a, b) => a.freq - b.freq);

    while (heap.length > 1) {

        let left = heap.shift();

        let right = heap.shift();

        let parent = new Node(null, left.freq + right.freq);

        parent.left = left;

        parent.right = right;

        heap.push(parent);

        heap.sort((a, b) => a.freq - b.freq);

    }

    return heap[0];

}

​

const frequencies = { 'a': 5, 'b': 9, 'c': 12, 'd': 13, 'e': 16, 'f': 45 };

const tree = buildHuffmanTree(frequencies);

console.log("Huffman Tree built successfully.");