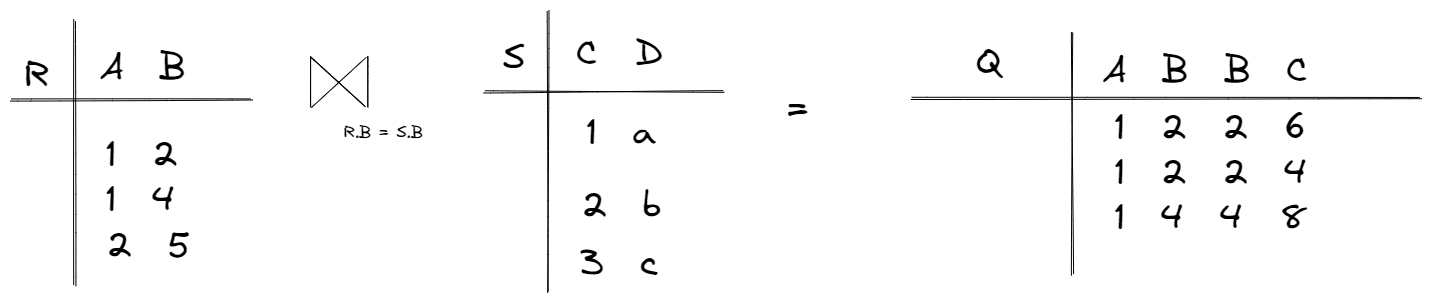Relational algebra

In database theory, relational algebra is a theory that uses algebraic structures with well-founded semantics for modeling data, and defining queries on it. The main premise of relational algebra is to define operators that transform one or more input relations to an output relation.

A relational algebra expression:

• takes as input one or more relations
• applies a sequence of operations
• returns a relation as output

There are a few defined operations in relational algebra, that are associated with their own symbols from the Greek alphabet.

1. Projection (π) - π set of attributes(relation) Chooses some of the columns, for example : π A1,...,An ( R ) takes only the values of attributes A1, . . . , An for each tuple in R

2. Selection (σ) - σ condition(relation) Chooses rows satisfying a given condition, for example: σθ ( R ) takes only the tuples in R for which θ is satisfied

1term := attribute | constant 
2θ := term op term with op ∈ {=, 6=, >, <, >, 6} | θ ∧ θ | θ ∨ θ | ¬θ

If we do not have attribute names (hence, we can only reference columns via their component number), then we need to have a special symbol, say $, in front of a component number. Thus, $4 > 100 is a meaningful basic clause $1 =“Apto” is a meaningful basic clause, and so on. Consecutive selections can be combined into a single one:

1σθ1 σθ2 ( R )  =  σθ1 ∧ θ2 ( R )

3. Product (×) - RxS Concatenates each tuple of R with all the tuples of S

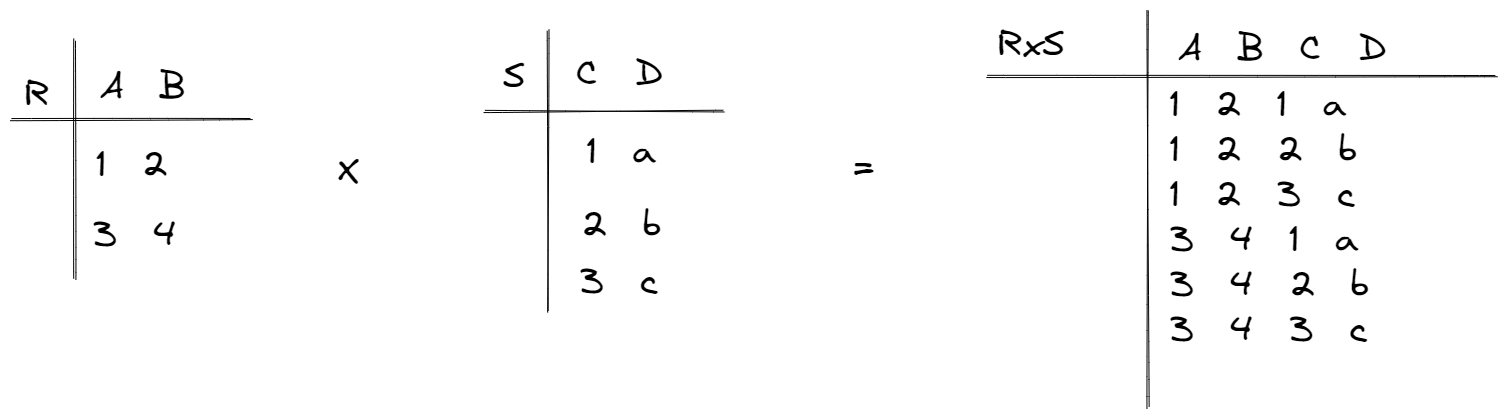
4. Renaming (ρ) - ρ replacements(relation), Gives a new name to some of the attributes of a relation, where a replacement has the form A → B Example:

1σCustID = CustID'(Customer × ρCustID→CustID'(Account))

5. Union (∪) - R ∪ S A binary operation whose result is a relation including the elements belonging to R, or to S, or both to R and S. The duplicates are removed. Example: Find the SSN of all the employees in department 5, or are supervising an employee in department 5.

1DEP5_EMPS ← σDNO=5 (EMPLOYEE) 
2RESULT1 ← π SSN(DEP5_EMPS) 
3RESULT2 ← πSUPERSSN(DEP5_EMPS) 
4RESULT ← RESULT1 ∪ RESULT2

6. Intersection (∩) - R ∩ S The result of intersection is a relation that has all the common elements of R and S.

7. Difference (−) - R-S SET DIFFERENCE (can be named also MINUS or EXCEPT) is a difference between the two sets. The result is a relation that has all the elements that exist in R, but do not exist in S.

Union and Intersection are commutative operations:

1R ∪ S = S ∪ R, and R ∩ S = S ∩ R

Union and intersection are also associative operations:

1R ∪ (S ∪ T) = (R ∪ S) ∪ T 
2(R ∩ S) ∩ T = R ∩ (S ∩ T)

Difference is not commutative, thus:

1R – S ≠ S – R

8. Join Join is a derived operation and can be expressed in terms of π , σ , × , ρ. It can be represented as a product, followed by a select, to identify and select related entities from two relations. Join combines this in a single operation. This is one of the most important operations in relational databases because it allows the combination of connected entities.