The Theory

Imagine a vast library, home to a plethora of books on myriad subjects. The library is organized into sections, each housing books on a particular topic. Now, you're the librarian, and you wish to quickly answer questions like:

• How many books are there in a specific range of sections?
• What's the thickest book between section A and section B?

Checking each book or even each section individually would be tedious. Enter the "Section Summary Card System" (or SSCS, because who doesn't love acronyms?). This system gives you a summarized view of every possible range of sections, allowing you to answer queries rapidly.

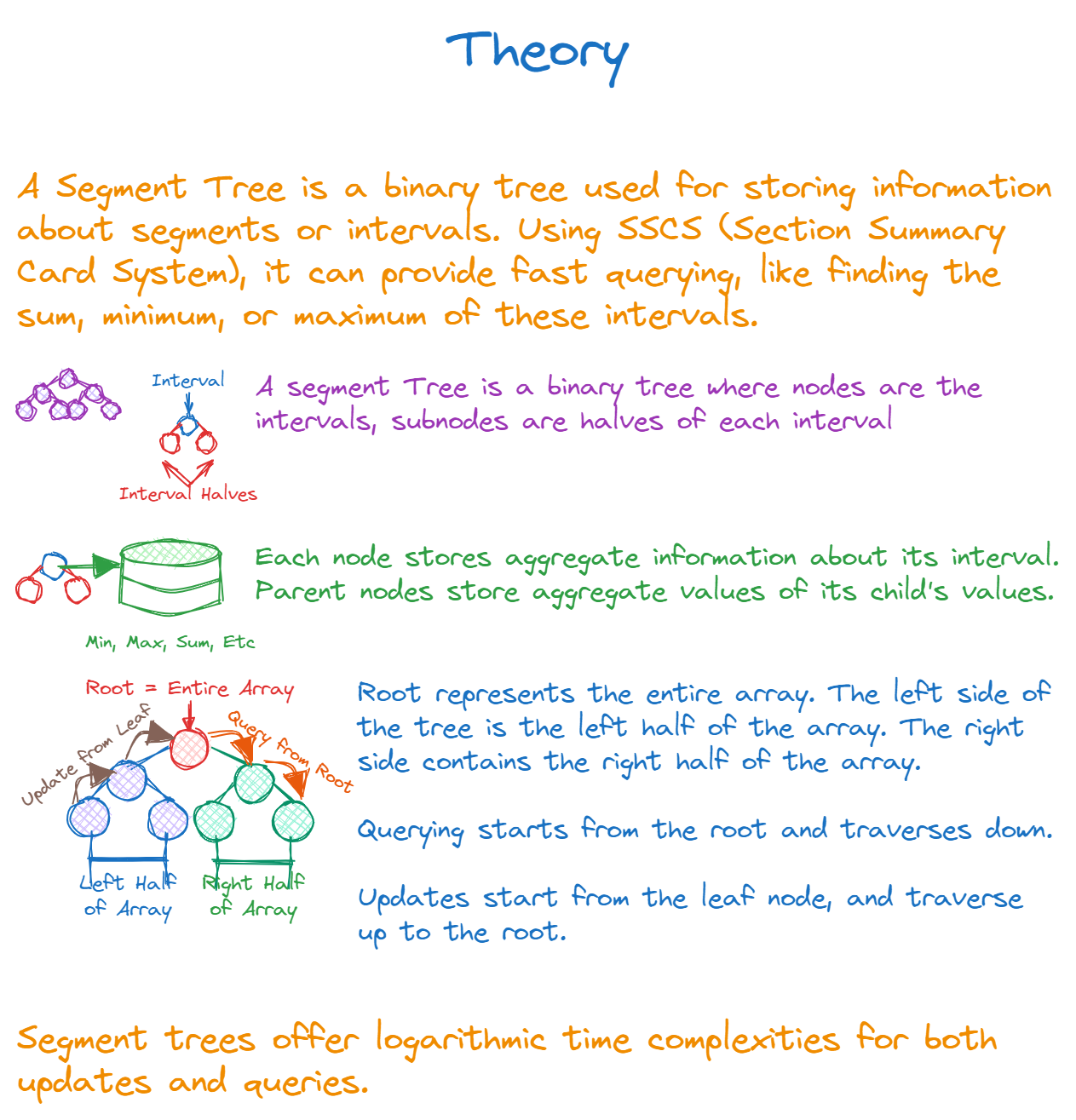
The Segment Tree is akin to this SCSS. It provides summarized information about various segments (or intervals) of an array, enabling efficient answers to range queries.

The Theoretical Dive

With the analogy in mind, let's understand the Segment Tree's core essence.

Structure: At its core, a Segment Tree is a binary tree. Each node represents an interval of an array, with the root representing the entire array. The two children of a node represent the two halves of the node's interval. This hierarchical structure ensures that we can access any sub-interval of the array in logarithmic time.

Storage: Each node in the Segment Tree stores aggregate information about its interval. This information could be the sum of elements in that interval, the maximum element, the minimum, etc. When we say "aggregate," it means that the information at a parent node can be derived from its children. For example, if nodes store sums, then the parent's value is the sum of its two children's values.

Building the Tree: The tree is constructed recursively. The process can be visualized as:

1. The root node represents the entire array.
2. Split the current interval into two halves.
3. The left child represents the left half, and the right child represents the right half.
4. Repeat the process for each child until you reach individual array elements.

Querying: To fetch information about a particular interval, we traverse the tree from the root. At each node, we decide:

1. If the node's interval lies entirely inside the query interval, fetch the node's value.
2. If the node's interval is outside the query interval, ignore it.
3. If the node's interval partially overlaps the query interval, split the query and delve deeper into both children.

Updates: When an element of the array changes, the tree nodes representing intervals containing that element must be updated. This update is propagated from the leaf node (representing a single element) up to the root.

Why Segment Trees?

With the availability of simpler data structures, why venture into the realm of Segment Trees? The answer lies in their power and efficiency. Segment Trees offer a unique blend of logarithmic time complexities for both updates and queries. They are versatile and can be adapted for various range-query problems beyond just sums, such as range minimums, maximums, and even gcds.