Implementation

Crafting Our Segment Tree

Let's roll up our sleeves and carve out this tree in Python:

1// javascript version
2class SegmentTree {
3    constructor(arr) {
4        this.n = arr.length;
5        this.tree = new Array(4 * this.n).fill(0);
6        this.build(arr, 1, 0, this.n-1);
7    }
8
9    build(arr, v, l, r) {
10        if (l === r) {
11            this.tree[v] = arr[l];
12        } else {
13            let m = Math.floor((l + r) / 2);
14            this.build(arr, v*2, l, m);
15            this.build(arr, v*2+1, m+1, r);
16            this.tree[v] = this.tree[v*2] + this.tree[v*2+1];
17        }
18    }
19}

You might be wondering, "What's this magic?" Let's break it down:

• We begin by initializing our tree to four times the size of our input array.
• The build function is where the magic happens. It recursively constructs our segment tree. If we're at a leaf node, we store the array element. Otherwise, we build the left and right subtrees and store their sum.

Understanding the Segment Tree with an Example

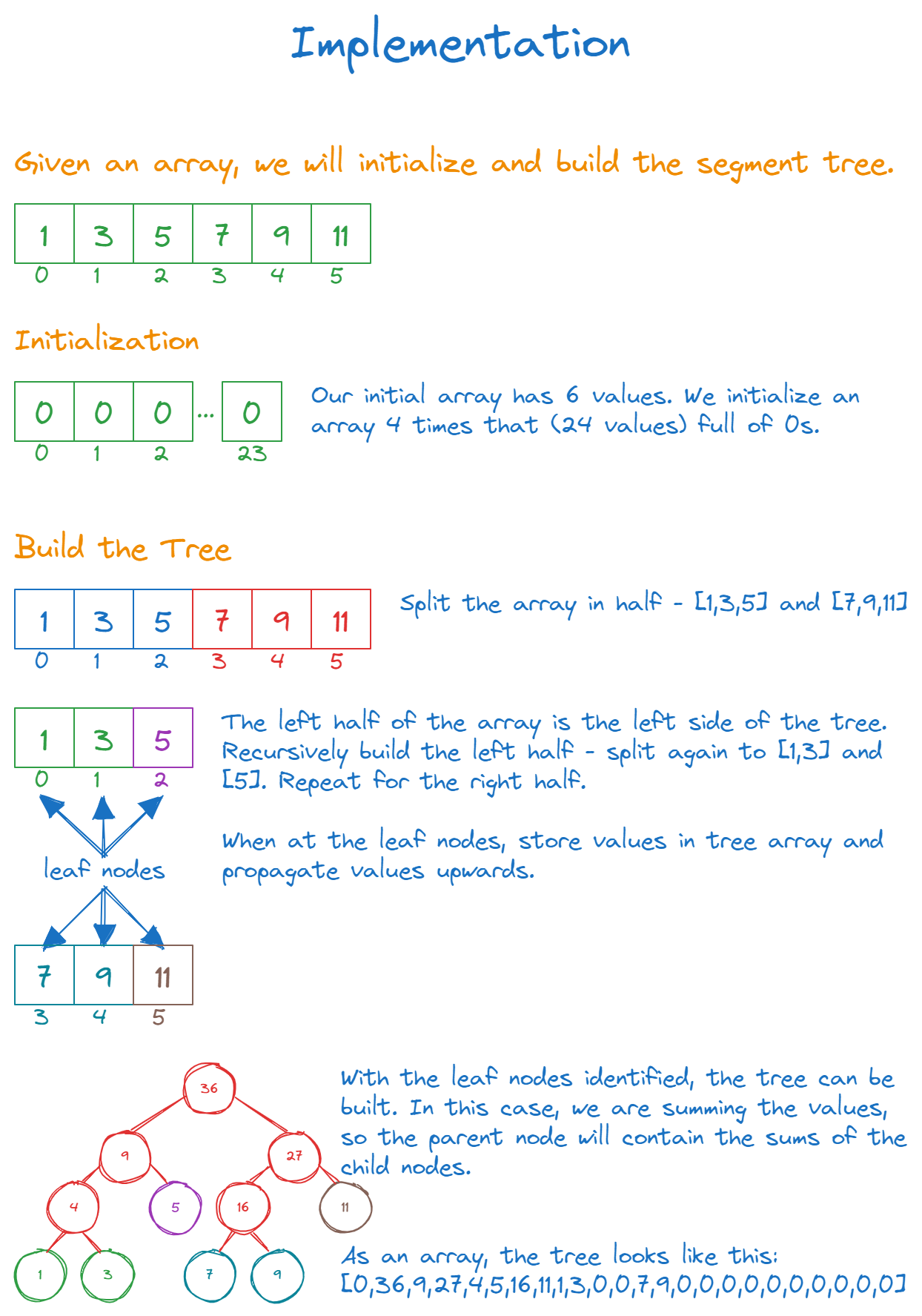
Consider an example array: arr = [1, 3, 5, 7, 9, 11].

Step 1: Initialization

When we instantiate our segment tree with this array, we initialize an array tree with zeros, which is four times the size of arr. This ensures that we have enough space to represent the tree. So our tree starts as:

1tree = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Step 2: Building the Tree

The build function starts working on the array. Since the input does not represent a single element (i.e., l is not equal to r), we find the middle of the array and recursively build for the left and right halves.

For our array, the process would look something like:

1. Start with the entire array: l=0, r=5 (entire array). Middle m=2.
2. Recursively build the left half: l=0, r=2 (elements [1, 3, 5]). Here again, we'd split this into two halves: [1, 3] and [5].
3. Continue this process until we reach individual elements.
4. Once we've reached individual elements (leaf nodes), we begin storing values in the tree array and then propagate those values upwards.

Visually, the tree array evolves as:

1Step 1 (Initialization): [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2Step 2 (Building for leaf nodes): [0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3Step 3 (Building upwards): [0, 0, 0, 0, 4, 5, 16, 11, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4Step 4 (Final tree after aggregating values): [0, 36, 9, 27, 4, 5, 16, 11, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Note: The above representation is a simplification. The tree's structure and values will vary based on the aggregation function used (in this case, sum).

By the end of the build process, our tree array has stored values at appropriate positions. The root of the tree (position 1 in the array) contains the aggregated value of the entire array. The left and right children of each node split this aggregated value further down into segments, and so on.

This segment tree structure allows us to efficiently query a range of values (like the sum between two indices) and update individual values.