AlgoDaily - What Is A Segment Tree?

Home > Data Structures and Algorithms 🚀 > Climb Some Trees > What Is A Segment Tree?

Welcome to the realm of Segment Trees! If you've meandered through the pathways of data structures, you've likely bumped into various trees. But today, we're introducing a special kind of tree that's less talked about yet incredibly powerful: the Segment Tree.

What Exactly is a Segment Tree?

Imagine you're building the next big thing since sliced bread: an app that allows users to rate their bread slices (because, why not?). You need a quick way to query ratings within a range or update a rating. This is where a using a segment tree would shine.

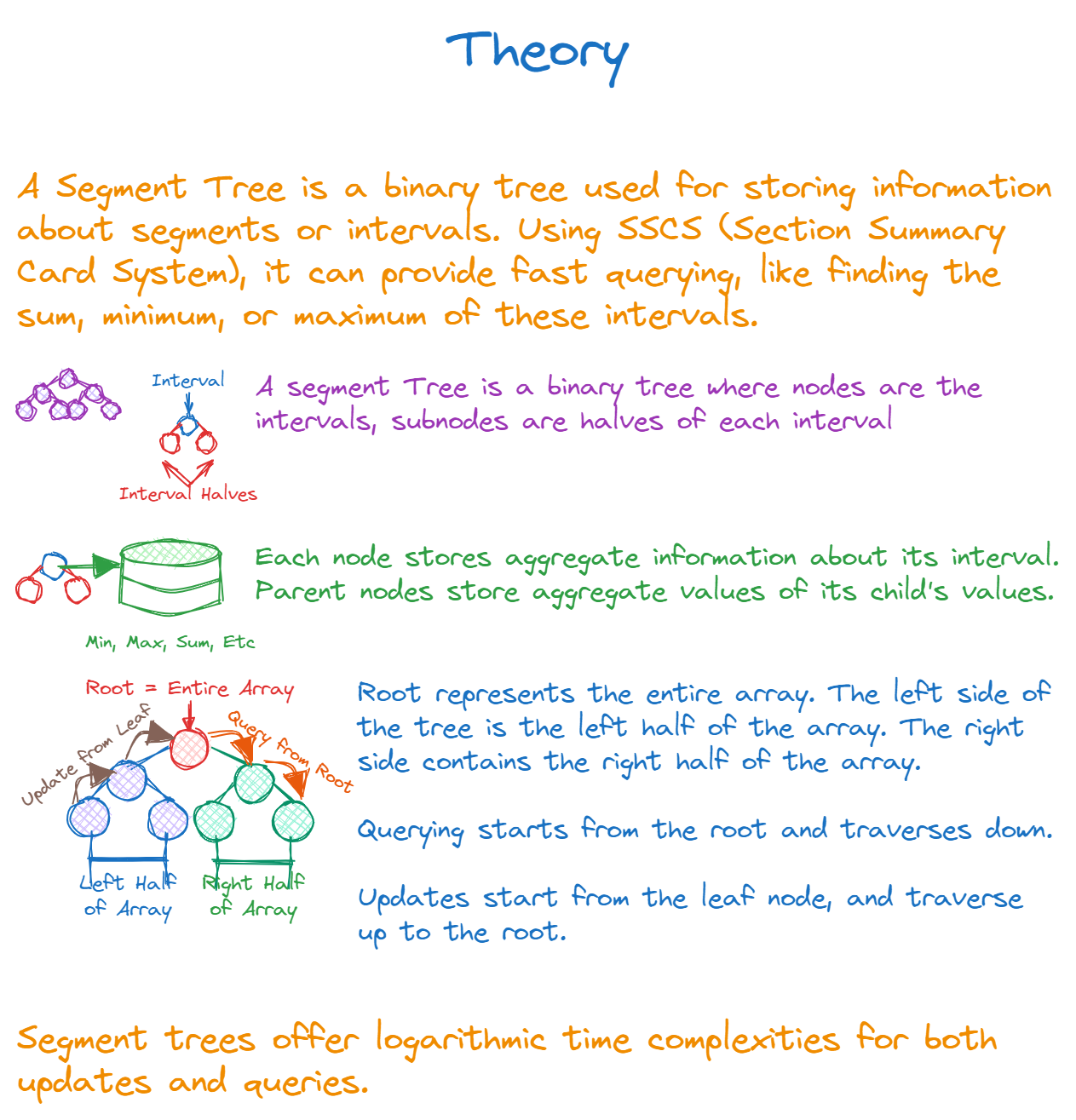
At its core, a Segment Tree is a binary tree used for storing information about segments or intervals. It facilitates faster querying, like finding the sum, minimum, or maximum of these intervals. It's the kind of tool you didn't know you needed until now.

The Theory

Imagine a vast library, home to a plethora of books on myriad subjects. The library is organized into sections, each housing books on a particular topic. Now, you're the librarian, and you wish to quickly answer questions like:

How many books are there in a specific range of sections?
What's the thickest book between section A and section B?

Checking each book or even each section individually would be tedious. Enter the "Section Summary Card System" (or SSCS, because who doesn't love acronyms?). This system gives you a summarized view of every possible range of sections, allowing you to answer queries rapidly.

The Segment Tree is akin to this SCSS. It provides summarized information about various segments (or intervals) of an array, enabling efficient answers to range queries.

The Theoretical Dive

With the analogy in mind, let's understand the Segment Tree's core essence.

Structure: At its core, a Segment Tree is a binary tree. Each node represents an interval of an array, with the root representing the entire array. The two children of a node represent the two halves of the node's interval. This hierarchical structure ensures that we can access any sub-interval of the array in logarithmic time.

Storage: Each node in the Segment Tree stores aggregate information about its interval. This information could be the sum of elements in that interval, the maximum element, the minimum, etc. When we say "aggregate," it means that the information at a parent node can be derived from its children. For example, if nodes store sums, then the parent's value is the sum of its two children's values.

Building the Tree: The tree is constructed recursively. The process can be visualized as:

The root node represents the entire array.
Split the current interval into two halves.
The left child represents the left half, and the right child represents the right half.
Repeat the process for each child until you reach individual array elements.

Querying: To fetch information about a particular interval, we traverse the tree from the root. At each node, we decide:

If the node's interval lies entirely inside the query interval, fetch the node's value.
If the node's interval is outside the query interval, ignore it.
If the node's interval partially overlaps the query interval, split the query and delve deeper into both children.

Updates: When an element of the array changes, the tree nodes representing intervals containing that element must be updated. This update is propagated from the leaf node (representing a single element) up to the root.

Why Segment Trees?

With the availability of simpler data structures, why venture into the realm of Segment Trees? The answer lies in their power and efficiency. Segment Trees offer a unique blend of logarithmic time complexities for both updates and queries. They are versatile and can be adapted for various range-query problems beyond just sums, such as range minimums, maximums, and even gcds.

Implementation

Crafting Our Segment Tree

Let's roll up our sleeves and carve out this tree in Python:

1// java version
2public class SegmentTree {
3    private int[] tree;
4    private int n;
5
6    public SegmentTree(int[] arr) {
7        this.n = arr.length;
8        this.tree = new int[4 * n];
9        build(arr, 1, 0, n-1);
10    }
11
12    private void build(int[] arr, int v, int l, int r) {
13        if (l == r) {
14            tree[v] = arr[l];
15        } else {
16            int m = (l + r) / 2;
17            build(arr, v*2, l, m);
18            build(arr, v*2+1, m+1, r);
19            tree[v] = tree[v*2] + tree[v*2+1];
20        }
21    }
22}

You might be wondering, "What's this magic?" Let's break it down:

We begin by initializing our tree to four times the size of our input array.
The build function is where the magic happens. It recursively constructs our segment tree. If we're at a leaf node, we store the array element. Otherwise, we build the left and right subtrees and store their sum.

Understanding the Segment Tree with an Example

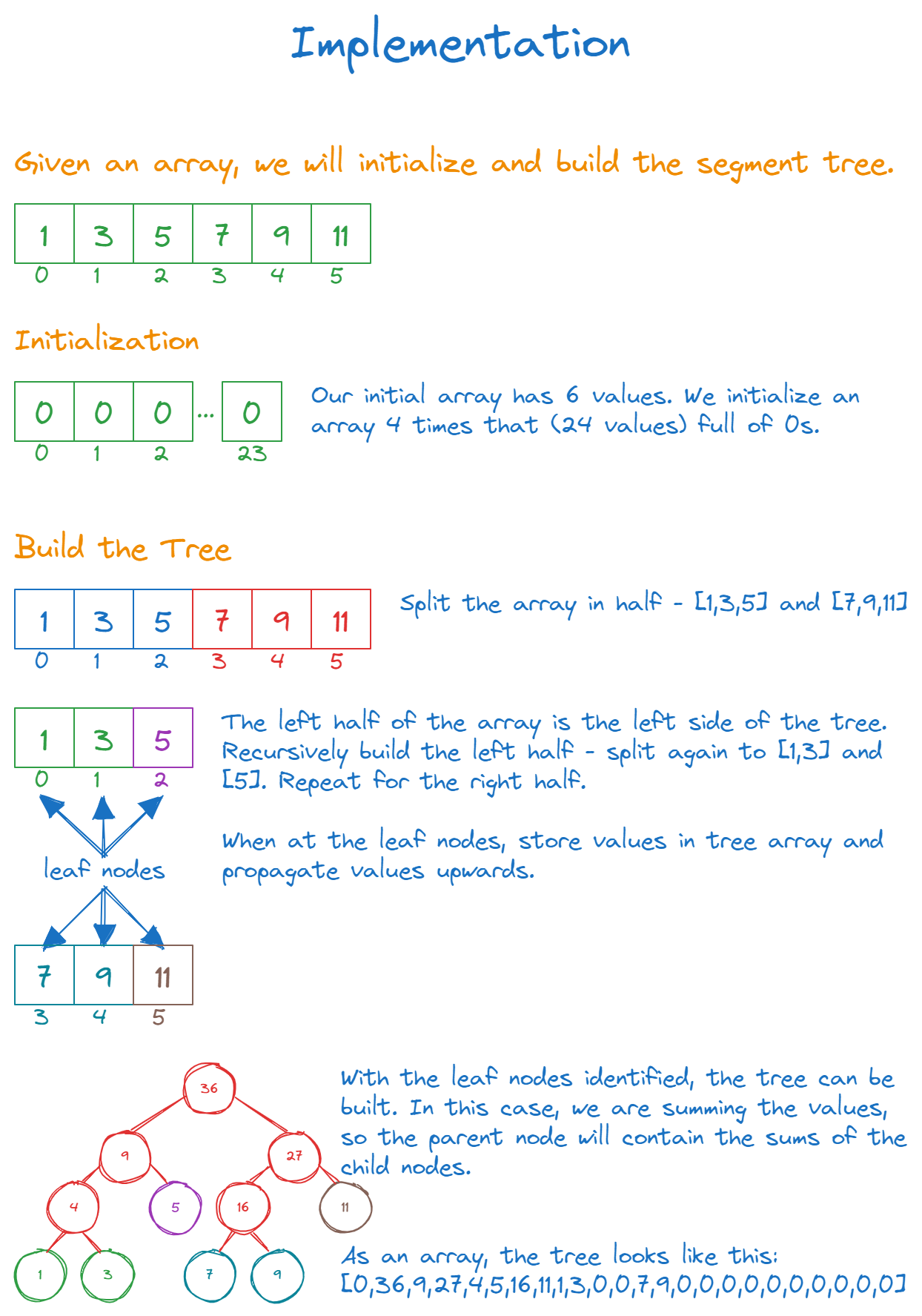
Consider an example array: arr = [1, 3, 5, 7, 9, 11].

Step 1: Initialization

When we instantiate our segment tree with this array, we initialize an array tree with zeros, which is four times the size of arr. This ensures that we have enough space to represent the tree. So our tree starts as:

SNIPPET

1tree = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Step 2: Building the Tree

The build function starts working on the array. Since the input does not represent a single element (i.e., l is not equal to r), we find the middle of the array and recursively build for the left and right halves.

For our array, the process would look something like:

Start with the entire array: l=0, r=5 (entire array). Middle m=2.
Recursively build the left half: l=0, r=2 (elements [1, 3, 5]). Here again, we'd split this into two halves: [1, 3] and [5].
Continue this process until we reach individual elements.
Once we've reached individual elements (leaf nodes), we begin storing values in the tree array and then propagate those values upwards.

Visually, the tree array evolves as:

SNIPPET

1Step 1 (Initialization): [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2Step 2 (Building for leaf nodes): [0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3Step 3 (Building upwards): [0, 0, 0, 0, 4, 5, 16, 11, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4Step 4 (Final tree after aggregating values): [0, 36, 9, 27, 4, 5, 16, 11, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Note: The above representation is a simplification. The tree's structure and values will vary based on the aggregation function used (in this case, sum).

By the end of the build process, our tree array has stored values at appropriate positions. The root of the tree (position 1 in the array) contains the aggregated value of the entire array. The left and right children of each node split this aggregated value further down into segments, and so on.

This segment tree structure allows us to efficiently query a range of values (like the sum between two indices) and update individual values.

Querying Our Tree

With the tree built, it's time to extract some information from it!

1// java version
2public int query(int v, int l, int r, int ql, int qr) {
3    if (ql <= l && r <= qr) {
4        return tree[v];
5    }
6    if (qr < l || r < ql) {
7        return 0;
8    }
9    int m = (l + r) / 2;
10    return query(v*2, l, m, ql, qr) + query(v*2+1, m+1, r, ql, qr);
11}

Each version of the query function captures the same logic and functionality as your original Python function but in the respective languages.

This function allows you to ask, "Hey tree, can you tell me the sum between indices ql and qr?" And the tree, being the wise entity it is, either provides an answer or divides the task among its children.

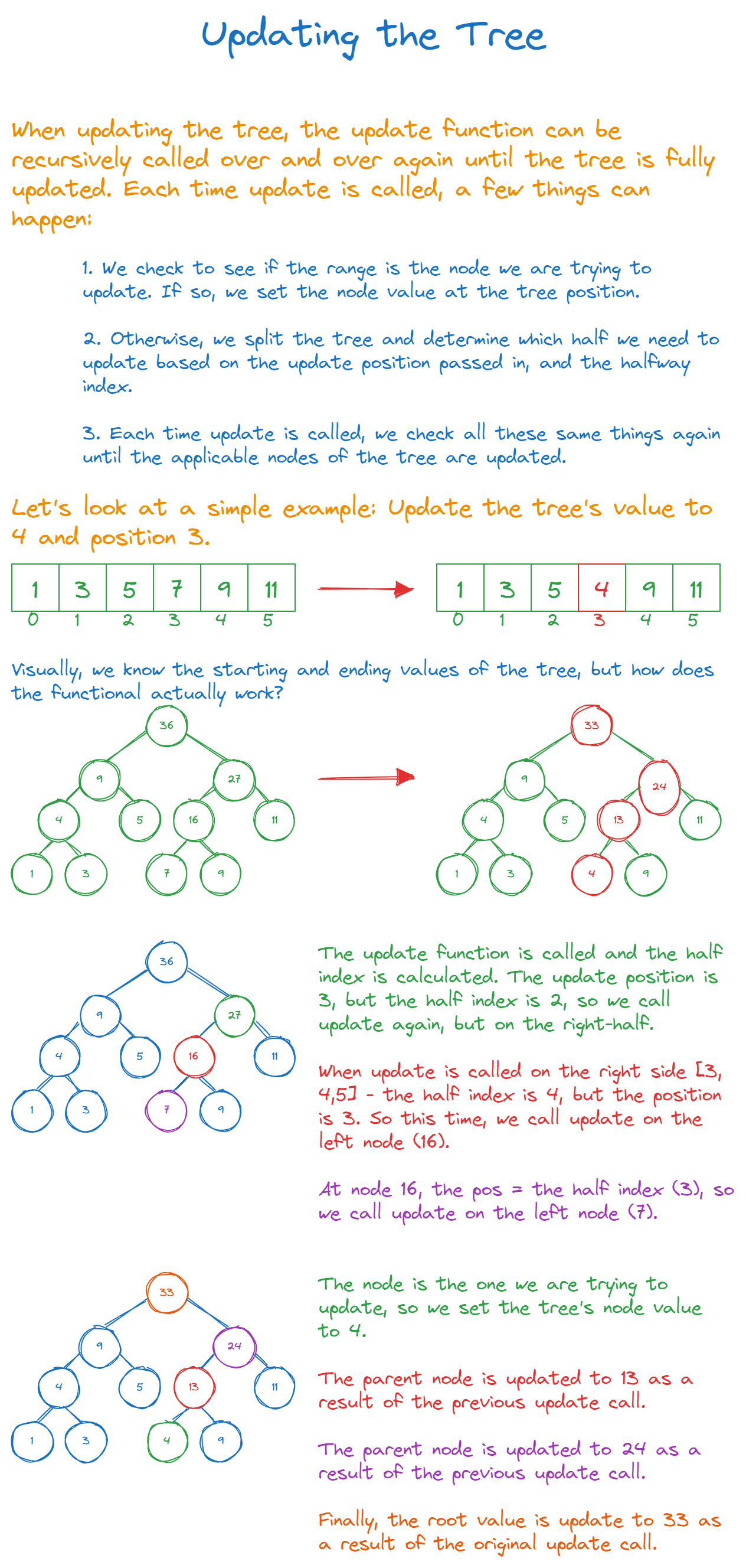
Updating: Because Change is the Only Constant

Sometimes, a bread slice gets extra crispy and its rating changes. We need to account for that.

1// java version
2public void update(int v, int l, int r, int pos, int val) {
3    if (l == r) {
4        tree[v] = val;
5    } else {
6        int m = (l + r) / 2;
7        if (pos <= m) {
8            update(v*2, l, m, pos, val);
9        } else {
10            update(v*2+1, m+1, r, pos, val);
11        }
12        tree[v] = tree[v*2] + tree[v*2+1];
13    }
14}

With this update method, we locate our slice, adjust its rating, and inform the tree about this delightful crispiness.

A Slice of Action

Let's witness our Segment Tree in action:

1// java version
2int[] ratings = {4, 3, 5, 2, 1};
3SegmentTree breadTree = new SegmentTree(ratings);
4
5System.out.println(breadTree.query(1, 0, breadTree.n-1, 1, 3));  // Output: 10 (Because 3 + 5 + 2 = 10)
6breadTree.update(1, 0, breadTree.n-1, 2, 4);  // The third slice's rating changed!
7System.out.println(breadTree.query(1, 0, breadTree.n-1, 1, 3));  // Output: 9 (Because 3 + 4 + 2 = 9)

Each version captures the logic and functionality of your original Python code, but in the respective languages.

And there you have it! Your bread slices are now neatly organized in a Segment Tree.

xxxxxxxxxx
}
 
public class Main {
    private int[] tree;
    private int n;
​
    Main(int[] arr) {
        this.n = arr.length;
        this.tree = new int[4 * n];
        build(arr, 1, 0, n-1);
    }
​
    private void build(int[] arr, int v, int l, int r) {
        if (l == r) {
            tree[v] = arr[l];
        } else {
            int m = (l + r) / 2;
            build(arr, v*2, l, m);
            build(arr, v*2+1, m+1, r);
            tree[v] = tree[v*2] + tree[v*2+1];
        }
    }
​
    public int query(int v, int l, int r, int ql, int qr) {
        if (ql <= l && r <= qr) {
            return tree[v];
        }
        if (qr < l || r < ql) {
            return 0;
        }
        int m = (l + r) / 2;

Conclusion

Segment Trees might initially seem like an intricate puzzle, but with a bit of practice and patience, they become an indispensable tool in your coding toolkit. They offer a beautiful blend of theory and practicality, making tasks involving array intervals seem like a breeze. Here's to more efficient coding and perfectly rated bread slices!

One Pager Cheat Sheet

A Segment Tree is a special binary tree data structure used for storing information about segments or intervals, facilitating faster querying like finding the sum, minimum, or maximum of these intervals.
A Segment Tree is a binary tree that provides summarized information about various segments of an array, allowing efficient responses to range queries; each node represents an array interval, storing aggregate information about that interval, and the tree is structured such that any sub-interval can be accessed in logarithmic time. The Segment Tree is built recursively, splitting intervals into halves represented by child nodes, and allows for quick queries and updates by traversing from the root node and updating from the leaf up. The Segment Tree stands out for its power and efficiency in complex data structures, offering logarithmic time complexities for both updates and queries, and flexibility for a variety of range-query problems.
The SegmentTree class in Python includes an initialization function that prepares a tree of four times the size of the original array, and a build function that recursively constructs the segment tree; if at a leaf node, the function stores the array element, otherwise, it constructs left and right subtrees and stores their sum. This allows efficient querying of a range of values and updating of individual values in the segment tree.
The query and update functions in the Segment Tree allow you to respectively retrieve the sum of the tree node values between two indices and adjust a tree node value, exemplified here with a bread rating system where bread slice ratings can be adjusted and their sum queried for.
Segment Trees are an invaluable coding tool that simplify tasks involving array intervals, blending theory and practicality for more efficient coding.