AlgoDaily - Design A Least Recently Used (LRU) Cache

Good evening! Here's our prompt for today.

A cache (pronounced cash) is a place of storage that allows for faster data retrieval. Separate from the main data storage, it's usually faster memory that houses frequently accessed values.

With a cache in place, when a client application needs to access data, it'll check the cache first before going to main memory. As an example, web browsers will typically download a page once, and refer to its cached assets in future calls to help speed up the experience.

To determine whether something should be cached, a few eviction strategies are used. IBM refers to eviction as "a feature where file data blocks in the cache are released when fileset usage exceeds the fileset soft quota, and space is created for new files". The process of releasing blocks is called eviction.

One of the most common is LRU, or Least Recently Used. It's exactly as it sounds-- we keep track of usage so that we can "evict" the least recently used key.

Can you implement a LRU Cache where the following code would properly work with some constraints?

1# initialize with a capacity of 3 keys
2cache = Cache(3)
3cache.put(1, 1)
4cache.put(2, 4)
5cache.put(3, 9)
6cache.get(1)      # returns 1
7cache.put(4, 16)  # evicts key 2
8cache.get(2)      # returns -1

The put and get methods should have a time complexity of O(1).

Constraints

The cache size will be <= 100000
The key and value will have values between -1000000000 and 1000000000

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
class Cache:
    def __init__(self, capacity):
        self.count = 0
        self.capacity = capacity
​
    def get(self, key):
        # fill in
        return
​
    def put(self, key, value):
        # fill in
        return
​
​
import unittest
​
​
class Test(unittest.TestCase):
    def test_1(self):
        cache = Cache(3)
        cache.put(1, 1)
        cache.put(2, 4)
        cache.put(3, 9)
        assert cache.get(1) == 1
​
        print("PASSED: Initialize a cache of size 3, and add/get items")
​
    def test_2(self):
        if not "cache" in vars():

Here's our guided, illustrated walk-through.

How do I use this guide?

Let's start by laying out our requirements. We're implementing a cache with a get method and a put method. There are several other methods that we want in a production cache class, but this will do for now.

get(key) needs to do a lookup of the key in the cache. If it does not find the key, we'll return a -1 for "not found".
put(key, val) needs to insert the key if it's not in the cache. If the cache has reached capacity, it needs to invalidate the least recently used key.

There are a few ways to have get and put operate in constant time. Let's think of data structures we can use that support quick access. One easy way is to use a hash table data structure, which enables lookups in O(1) time. We set the keys and values of the cache to be a hash table/hash map, and retrieval speed is taken care of.

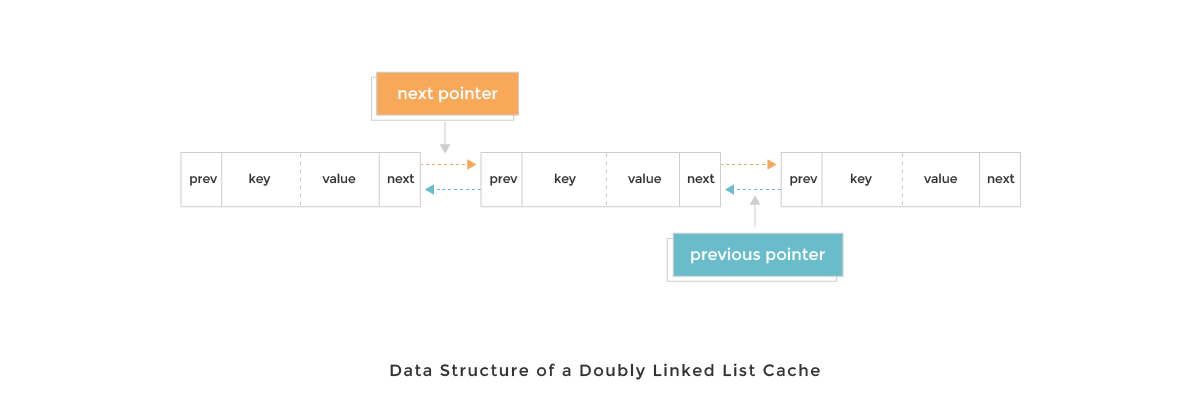
What about put? We'll also want our addition and eviction operations to run in constant time as well. A data structure we could introduce for this is a doubly linked list. A doubly linked list node is unique in that it has references to both the next node in the list, as well as the previous node. How does that help us? We'll see in a bit!

We get a decent hash table for free, built into many programming languages already. In the case of dynamic languages, we can use objects in JS or dictionaries in Python, so let's jump to implementing a doubly linked list. Here's what a DLinkedNode definition might look like:

1class DLinkedNode:
2	def __init__(self, key, val, pre, next):
3		self.key = key
4		self.val = val
5		self.pre = pre
6		self.next = next

With that, we can initialize doubly linked list nodes easily by calling new DLinkedNode(key, value, null, null).

In the Cache class, we'll also want to add the standard addNode and removeNode helper methods, as we'll be doing that quite a bit. addNode specifically adds a new node to the head of the doubly linked list. removeNode removes it place by manipulating the pre and next values of its neighbors.

1class DLinkedNode:
2	def __init__(self, key, val, pre, next):
3		self.key = key
4		self.val = val
5		self.pre = pre
6		self.next = next
7
8# for our Cache class
9def addNode(node):
10    node.pre = self.head
11    node.next = self.head.next
12    self.head.next.pre = node
13    self.head.next = node
14
15def removeNode(node):
16	# take a node's predecessor
17	pre = node.pre
18	# find the node after it
19	next = node.next
20	# assign the predecessor's "next" node as the one after current
21	pre.next = next
22	next.pre = pre

Now, when we new up a Cache instance, we'll want certain things predefined in the constructor. Let's flesh that out:

We'll need a reference to the capacity
A count for the number of keys we have
The cache via a hash table itself
References to the heads and tails of the doubly linked list

1class Cache:
2    def __init__(capacity):
3        self.count = 0
4        self.capacity = capacity
5        self.cache = {}
6        self.head = DLinkedNode()
7        self.head.pre = null
8        self.tail = DLinkedNode()
9        self.tail.next = None
10        self.head.next = self.tail
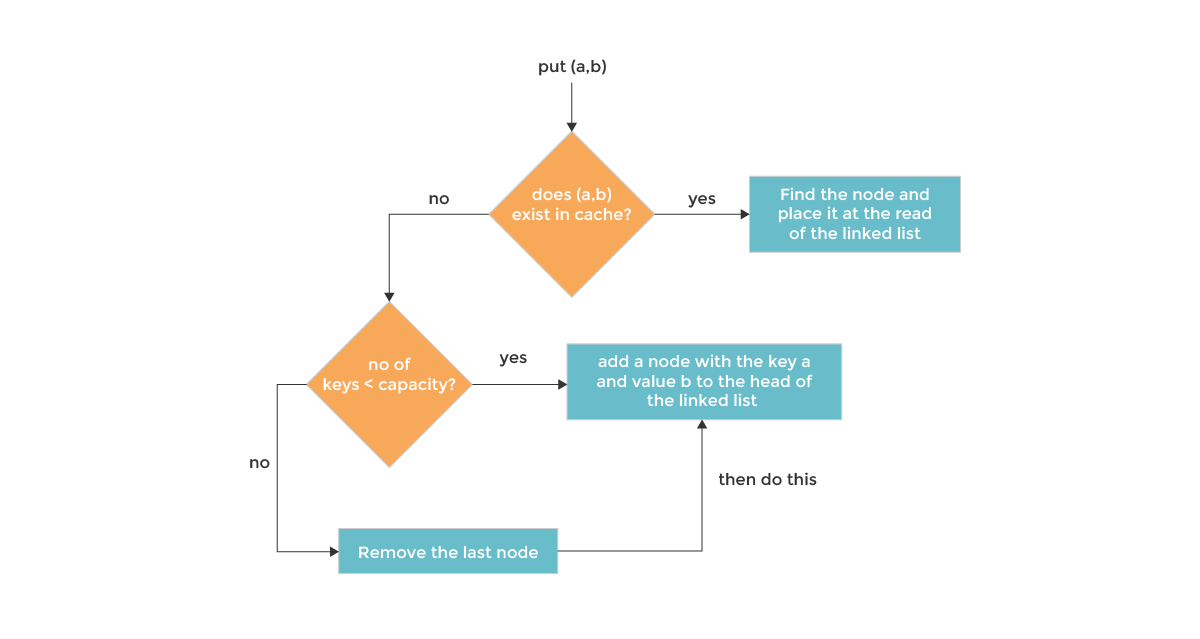
11        self.tail.pre = self.head

We're now in business. Let's start adding stuff by implementing the put method. put should check if the value exists or not in this.cache based on the key. If it doesn't, we can add it in.

However, it's not enough to just add it in-- the whole reason for using a doubly linked list is also to see the order of use. Thus, if we're adding a new value, it means that it's the most recently used, and we should thus move it to the front of the linked list. This serves to be an indication that we should NOT evict it.

put checks if the node is in the cache. If it's not, we create a new node in the doubly linked list (added to the head), and increment our length. We also check at this point if we're over capacity-- if we are, we get rid of the node at the tail, as it's the least recently used.

Alternatively, if the node already exists, we simply overwrite the existing node value and move it to the start.

1class Cache:
2    def __init__(capacity):
3        self.count = 0
4        self.capacity = capacity
5        self.cache = {}
6        self.head = DLinkedNode()
7        self.head.pre = null
8        self.tail = DLinkedNode()
9        self.tail.next = None
10        self.head.next = self.tail
11        self.tail.pre = self.head
12
13    def put(key, value):
14        node = self.cache[key]
15        if not node:
16            new_node = DLinkedNode(key, value, None, None)
17            self.cache[key] = new_node
18            self.addNode(new_node)
19            self.count += 1
20            # the overcapacity scenario
21            # evict the value at the end of the linked list
22            if self.count > self.capacity:
23                tail = self.popTail()
24                self.cache.pop(tail.key)
25                self.count -= 1
26        else:
27            node.val = value
28            # move to head as it's the most recently used
29            self.moveToHead(node)

Two helper functions are used above, one of which is moveToHead. This simply removes the node and re-adds it to the front, moving it ahead and letting us know it was the most recently used key.

1def moveToHead(self, node):
2    self.removeNode(node)
3    self.addNode(node)

Notice we also used a popTail method-- this function will be used for evicting nodes.

1def popTail(node):
2    pre = self.tail.pre
3    self.removeNode(pre)
4    return pre

Let's implement get! All get needs to do is find a key in this.cache. If found, we moveToHead to let keep it as the most recently used key, and return it. Otherwise, we return -1.

1def get(key):
2    node = this.cache[key]
3    if not node:
4        return -1
5    self.moveToHead(node)
6    return node.val

Not too bad! Let's see it all put together.

One Pager Cheat Sheet

Yes, it is possible to implement a LRU Cache with the mentioned constraints, where the put and get methods have a time complexity of O(1).
We are setting up a cache that has a get and put method using a hash table and doubly linked list data structure for lookups and insertion in constant time.
We can dynamically construct a DLinkedNode and use addNode and removeNode to add and remove nodes to/from the head of a doubly linked list.
We need to new up a Cache instance with reference to the capacity, a count for keys, the cache itself, and references to the heads and tails of the doubly linked list.
We put the new value in the cache and move it to the front of the doubly linked list if it exists, or create a new node if it doesn't, as well as evict nodes from the tail if we're over capacity to ensure the order of use is maintained.
The moveToHead function removes and re-adds a node to the front of a list, letting us know it was the most recently used key.
We get a key from the cache and moveToHead if found, otherwise return -1.
The performance of the bold new product was "not too bad".

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
    print("Nice job, 2/2 tests passed!")
 
class DLinkedNode:
    def __init__(self, key, val, pre=None, next=None):
        self.key = key
        self.val = val
        self.pre = pre
        self.next = next
​
​
class Cache:
    def __init__(self, capacity):
        self.count = 0
        self.capacity = capacity
        self.cache = {}
        self.head = DLinkedNode(0, 0)
        self.tail = DLinkedNode(0, 0)
        self.head.pre = None
        self.head.next = self.tail
        self.tail.pre = self.head
        self.tail.next = None
​
    def get(self, key):
        if not key in self.cache:
            return -1
        node = self.cache[key]
        self.moveToHead(node)
        return node.val
​
    def put(self, key, value):
        if not key in self.cache:
            newNode = DLinkedNode(key, value)
            self.cache[key] = newNode
            self.addNode(newNode)

Alright, well done! Try another walk-through.

If you had any problems with this tutorial, check out the main forum thread here.