Good morning! Here's our prompt for today.
A cache (pronounced cash) is a place of storage that allows for faster data retrieval. Separate from the main data storage, it's usually faster memory that houses frequently accessed values.
With a cache in place, when a client application needs to access data, it'll check the cache first before going to main memory. As an example, web browsers will typically download a page once, and refer to its cached assets in future calls to help speed up the experience.
To determine whether something should be cached, a few eviction strategies are used. IBM refers to eviction as "a feature where file data blocks in the cache are released when fileset usage exceeds the fileset soft quota, and space is created for new files". The process of releasing blocks is called eviction.
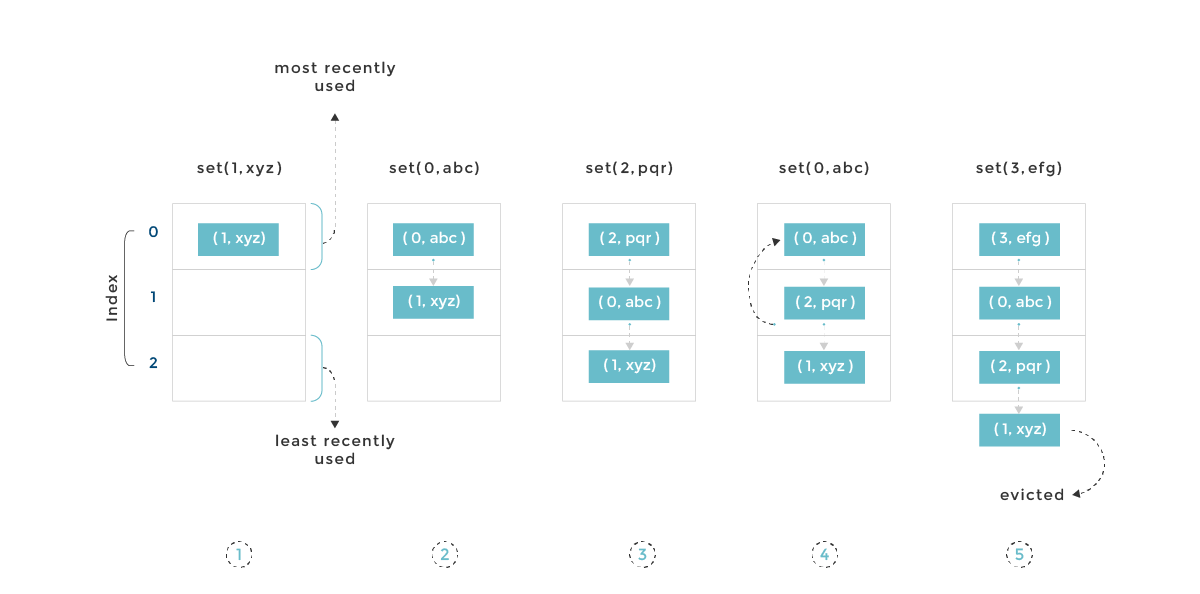
One of the most common is LRU, or Least Recently Used. It's exactly as it sounds-- we keep track of usage so that we can "evict" the least recently used key.
Can you implement a LRU Cache where the following code would properly work with some constraints?
1// initialize with a capacity of 3 keys
2const cache = new Cache(3);
3cache.put(1, 1);
4cache.put(2, 4);
5cache.put(3, 9);
6cache.get(1); // returns 1
7cache.put(4, 16); // evicts key 2
8cache.get(2); // returns -1The put and get methods should have a time complexity of O(1).
Constraints
- The cache size will be <=
100000 - The
keyandvaluewill have values between-1000000000and1000000000
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxvar assert = require('assert');class Cache { constructor(capacity) { // do something }}try { var cache = new Cache(3); cache.put(1, 1); cache.put(2, 4); cache.put(3, 9); assert.equal(cache.get(1), 1); console.log( 'PASSED: Initialize a cache of size 3, and run `cache.put(1, 1); cache.put(2, 4); cache.put(3, 9);`. `cache.get(1)` should return 1' );} catch (err) { console.log(err);}try { cache.put(4, 16); assert.equal(cache.get(2), -1); console.log('PASSED: ' + '`cache.put(4, 16);` should evict key `2`');} catch (err) { console.log(err);Here's how we would solve this problem...
How do I use this guide?
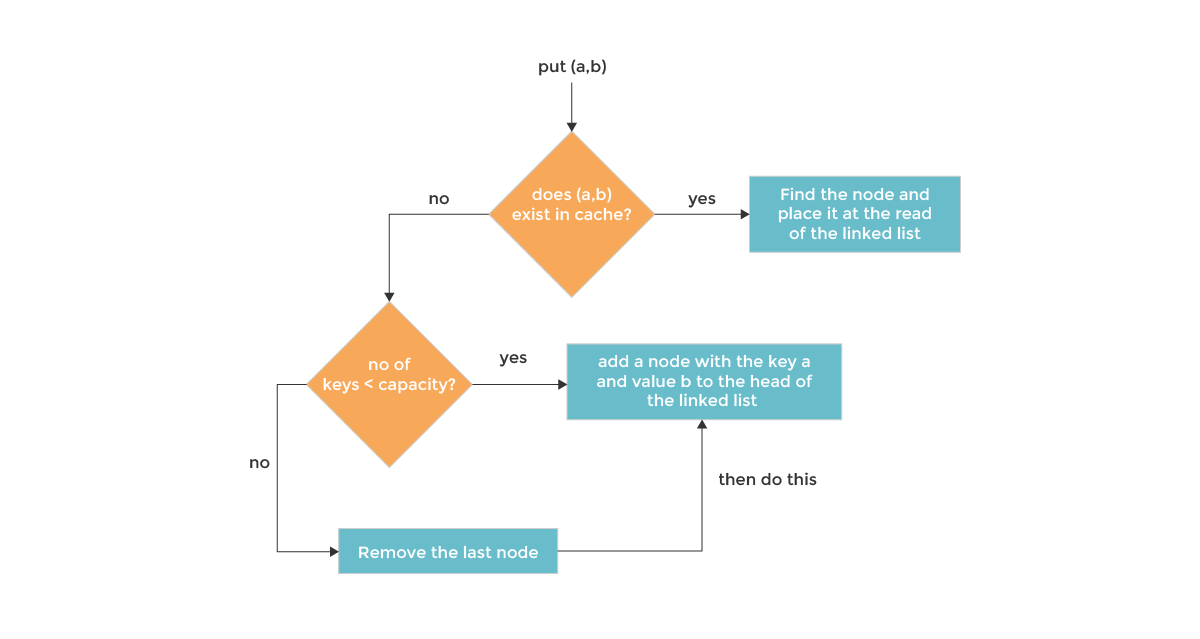
Let's start by laying out our requirements. We're implementing a cache with a get method and a put method. There are several other methods that we want in a production cache class, but this will do for now.
get(key)needs to do a lookup of the key in the cache. If it does not find the key, we'll return a-1for "not found".put(key, val)needs to insert the key if it's not in the cache. If thecachehas reached capacity, it needs to invalidate the least recently used key.
There are a few ways to have get and put operate in constant time. Let's think of data structures we can use that support quick access. One easy way is to use a hash table data structure, which enables lookups in O(1) time. We set the keys and values of the cache to be a hash table/hash map, and retrieval speed is taken care of.
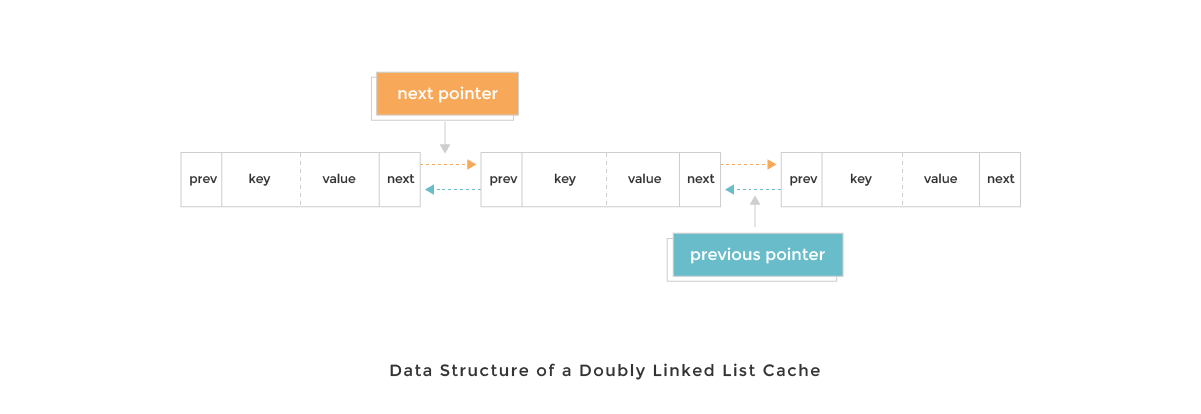
What about put? We'll also want our addition and eviction operations to run in constant time as well. A data structure we could introduce for this is a doubly linked list. A doubly linked list node is unique in that it has references to both the next node in the list, as well as the previous node. How does that help us? We'll see in a bit!
We get a decent hash table for free, built into many programming languages already. In the case of dynamic languages, we can use objects in JS or dictionaries in Python, so let's jump to implementing a doubly linked list. Here's what a DLinkedNode definition might look like:
1class DLinkedNode {
2 constructor(key, val, pre, next) {
3 this.key = key;
4 this.val = val;
5 this.pre = pre;
6 this.next = next;
7 }
8}With that, we can initialize doubly linked list nodes easily by calling new DLinkedNode(key, value, null, null).
In the Cache class, we'll also want to add the standard addNode and removeNode helper methods, as we'll be doing that quite a bit. addNode specifically adds a new node to the head of the doubly linked list. removeNode removes it place by manipulating the pre and next values of its neighbors.
1class DLinkedNode {
2 constructor(key, val, pre, next) {
3 this.key = key;
4 this.val = val;
5 this.pre = pre;
6 this.next = next;
7 }
8}
9
10// for our Cache class
11addNode(node) {
12 node.pre = this.head;
13 node.next = this.head.next;
14 this.head.next.pre = node;
15 this.head.next = node;
16};
17
18removeNode(node) {
19 // take a node's predecessor
20 const pre = node.pre;
21 // find the node after it
22 const next = node.next;
23 // assign the predecessor's "next" node as the one after current
24 pre.next = next;
25 next.pre = pre;
26};Now, when we new up a Cache instance, we'll want certain things predefined in the constructor. Let's flesh that out:
- We'll need a reference to the capacity
- A
countfor the number of keys we have - The
cachevia a hash table itself - References to the heads and tails of the doubly linked list
1class Cache {
2 constructor(capacity) {
3 this.count = 0;
4 this.capacity = capacity;
5 this.cache = {};
6 this.head = new DLinkedNode();
7 this.head.pre = null;
8 this.tail = new DLinkedNode();
9 this.tail.next = null;
10 this.head.next = this.tail;
11 this.tail.pre = this.head;
12 }
13}We're now in business. Let's start adding stuff by implementing the put method. put should check if the value exists or not in this.cache based on the key. If it doesn't, we can add it in.
However, it's not enough to just add it in-- the whole reason for using a doubly linked list is also to see the order of use. Thus, if we're adding a new value, it means that it's the most recently used, and we should thus move it to the front of the linked list. This serves to be an indication that we should NOT evict it.
put checks if the node is in the cache. If it's not, we create a new node in the doubly linked list (added to the head), and increment our length. We also check at this point if we're over capacity-- if we are, we get rid of the node at the tail, as it's the least recently used.
Alternatively, if the node already exists, we simply overwrite the existing node value and move it to the start.
1class Cache {
2 constructor(capacity) {
3 this.count = 0;
4 this.capacity = capacity;
5 this.cache = {};
6 this.head = new DLinkedNode();
7 this.head.pre = null;
8 this.tail = new DLinkedNode();
9 this.tail.next = null;
10 this.head.next = this.tail;
11 this.tail.pre = this.head;
12 }
13
14 put(key, value) {
15 const node = this.cache[key];
16 if (!node) {
17 const newNode = new DLinkedNode(key, value, null, null);
18 this.cache[key] = newNode;
19 this.addNode(newNode);
20 this.count++;
21 // the overcapacity scenario
22 // evict the value at the end of the linked list
23 if (this.count > this.capacity) {
24 const tail = this.popTail();
25 delete this.cache[tail.key];
26 this.count--;
27 }
28 } else {
29 node.val = value;
30 // move to head as it's the most recently used
31 this.moveToHead(node);
32 }
33 }
34}Two helper functions are used above, one of which is moveToHead. This simply removes the node and re-adds it to the front, moving it ahead and letting us know it was the most recently used key.
1moveToHead(node) {
2 this.removeNode(node);
3 this.addNode(node);
4};Notice we also used a popTail method-- this function will be used for evicting nodes.
1popTail(node) {
2 const pre = this.tail.pre;
3 this.removeNode(pre);
4 return pre;
5}Let's implement get! All get needs to do is find a key in this.cache. If found, we moveToHead to let keep it as the most recently used key, and return it. Otherwise, we return -1.
1get(key) {
2 const node = this.cache[key];
3 if (!node) {
4 return -1;
5 }
6 this.moveToHead(node);
7 return node.val;
8};Not too bad! Let's see it all put together.
One Pager Cheat Sheet
- Yes, it is possible to implement a
LRU Cachewith the mentioned constraints, where theputandgetmethods have a time complexity ofO(1). - We are setting up a
cachethat has agetandputmethod using ahash tableand doublylinked listdata structurefor lookups and insertion in constant time. - We can dynamically construct a
DLinkedNodeand useaddNodeandremoveNodeto add and remove nodes to/from the head of a doubly linked list. - We need to
newup aCacheinstance with reference to the capacity, acountfor keys, thecacheitself, and references to the heads and tails of the doubly linked list. - We
putthe new value in thecacheand move it to the front of thedoubly linked listif it exists, or create a new node if it doesn't, as well as evict nodes from the tail if we're over capacity to ensure the order of use is maintained. - The
moveToHeadfunctionremovesandre-addsa node to the front of a list, letting us know it was the most recently used key. - We
getakeyfrom thecacheandmoveToHeadif found, otherwise return-1. - The
performanceof the bold newproductwas "not too bad".
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx}var assert = require('assert');class Cache { constructor(capacity) { this.count = 0; this.capacity = capacity; this.cache = {}; this.head = new DLinkedNode(); this.head.pre = null; this.tail = new DLinkedNode(); this.tail.next = null; this.head.next = this.tail; this.tail.pre = this.head; } get(key) { const node = this.cache[key]; if (!node) { return -1; } this.moveToHead(node); return node.val; } put(key, value) { const node = this.cache[key]; if (!node) { const newNode = new DLinkedNode(key, value, null, null); this.cache[key] = newNode; this.addNode(newNode); this.count++; if (this.count > this.capacity) {Got more time? Let's keep going.
If you had any problems with this tutorial, check out the main forum thread here.

