Good evening! Here's our prompt for today.

How would you write a function to detect a substring in a string?

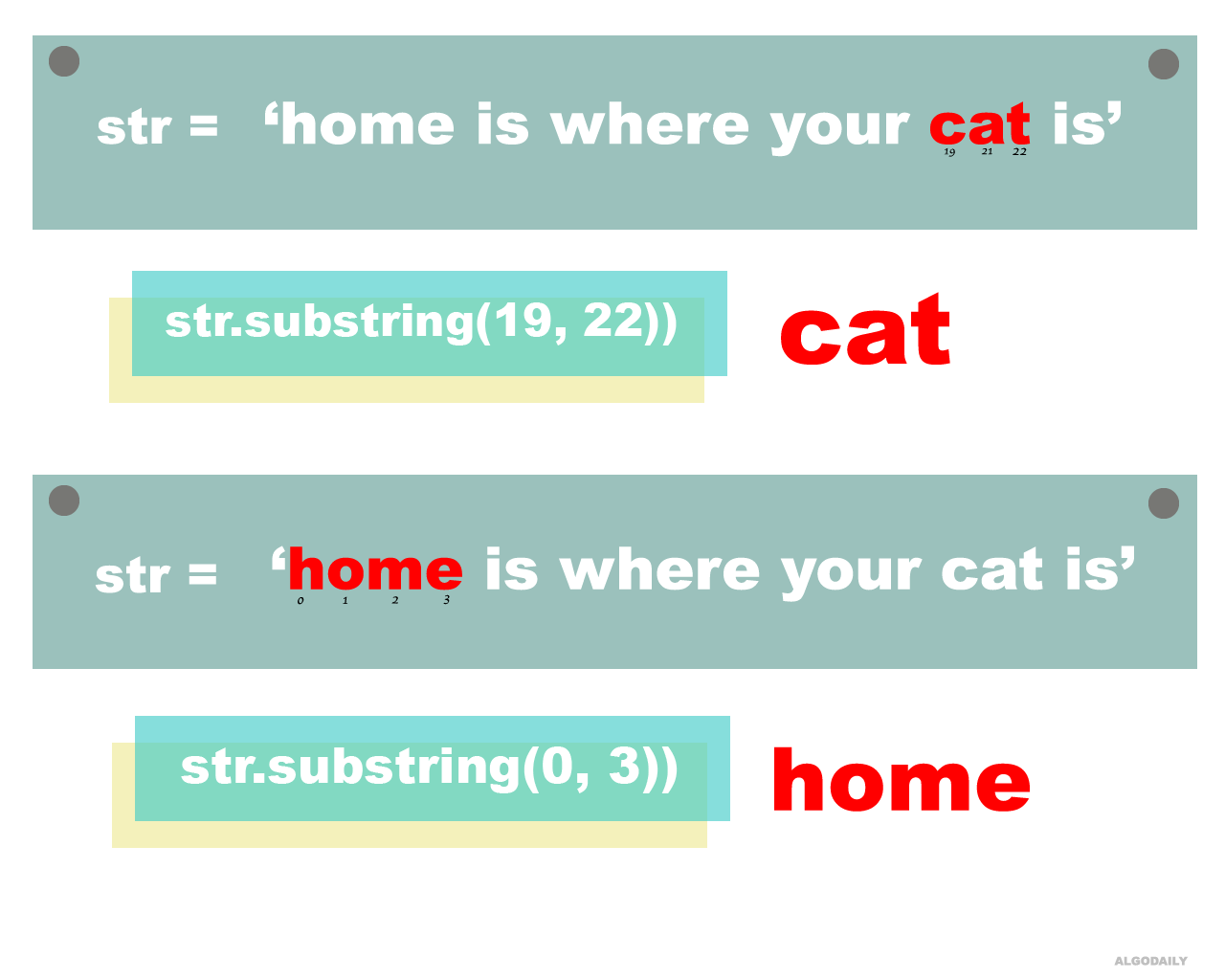
If the substring can be found in the string, return the index at which it starts. Otherwise, return -1.

1function detectSubstring(str, subStr) {
2  return -1;
3}

Important-- do not use the native String class's built-in substring or substr method. This exercise is to understand the underlying implementation of that method.

Constraints

• Length of both the given strings <=100000
• The strings would never be null
• The strings will only consist of lowercase letters
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

def detectSubstring(txt, subStr):

    # fill in

    return -1

​

​

import unittest

​

​

class Test(unittest.TestCase):

    def test_1(self):

        assert detectSubstring("thepigflewwow", "flew") == 6

        print("PASSED: `detectSubstring('thepigflewwow', 'flew')` should return `6`")

​

    def test_2(self):

        assert detectSubstring("twocanplay", "two") == 0

        print("PASSED: `detectSubstring('twocanplay', 'two')` should return `0`")

​

    def test_3(self):

        assert detectSubstring("wherearemyshorts", "pork") == -1

        print(

            "PASSED: `detectSubstring('wherearemyshorts', 'pork')` should return `-1`"

        )

​

​

if __name__ == "__main__":

    unittest.main(verbosity=2)

    print("Nice job, 3/3 tests passed!")

​

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

So we'd write a for-loop and check that each index is equal until the shorter word is completed.

What if we wanted to know if graph was in geography? We would still write a for-loop that compares the characters at each index, but we need to account for if there is a match later on.

Here, we can use the two-pointer technique we learned about prior! Why don't we use another pointer for the purpose of seeing how far we can "extend our match" when we find an initial one?

xxxxxxxxxx

idx_of_start = 0

j = 0

s = 'digginn'

sub_s = 'inn'

​

for i in range(len(s)):

  # if match, compare next character of sub_s with next of string

  if s[i] == sub_s[j]:

    j += 1

  else:

    j = 0

So given string geography and substring graph, we'd step it through like this:

1. g matches g, so j = 1
2. e does not match r, so j = 0
3. o does not match g, so j = 0
4. g does match g, so j = 1
5. r does match r, so j = 2
6. a does match a, so j = 3 and so on...

At the same time, we also need to keep track of the actual index that the match starts. The j index will help us get the matching, but we need a idxOfStart variable for just the start.

Putting it all together:

xxxxxxxxxx

idx_of_start = 0

j = 0

s = 'digginn'

sub_s = 'inn'

​

for i in range(len(s)):

  # if match, compare next character of sub_s with next of string

  if s[i] == sub_s[j]:

    j += 1

  else:

    j = 0

​

  # keep track of where match starts and ends

  if j == 0:

    idx_of_start = i

  elif j == len(sub_s):

    print(idx_of_start)

    # we know this is the start of match

There are still two slight issues with this code. Can you see what they are?

Let's take the examples of a string ggraph and substring graph. On the first iteration, g will match g, which is what we want. However, on the next iteration, we will try to match the second g in ggraph with r in graph.

What should happen is if we don't find a match, we ought to reset i a bit as well-- this is to accommodate duplicate characters. We can reset it specifically to the length of the last processed substring (or j).

The other thing is regarding the index of the start of the match-- we can simply get it from i - (subStr.length - 1). Note that you need to subtract 1 from the substring's length in order to get to the correct index.

Complexity of Final Solution

Let n be the length of the string. In the worst-case scenario, we iterate through all n characters of the string and do not find a match. Many of us will then declare that the time complexity is linear O(n). But think carefully, for each partial matching of substrings, we are traversing through the substring, and then again resetting to the initial pointer i.

To get a more clear insight into this, let's consider an example:

1str = "aaaaaa"
2subStr = "aab"

The final solution code of the method explained above is given.

xxxxxxxxxx

function detectSubstring(str, subStr) {

  let idxOfStart = 0,

    j = 0;

​

  for (i = 0; i < str.length; i++) {

    // if match, compare next character of subStr with next of string

    if (str[i] == subStr[j]) {

      j++;

      if (j == subStr.length) {

        return i - (subStr.length - 1);

      }

    } else {

      i -= j;

      j = 0;

    }

  }

​

  return -1;

}

As you can see, there are total 15 comparisons for the given test case. This is not close to the linear 6 comparison time complexity. In fact, this is a complexity of close to 6*3 comparisons. The reason for this is for each starting letter of the main string, we are comparing the whole substring and then resetting back to the initial character. See the image below:

So the time complexity will be O(mn) where m and n are the lengths of the string and substring. For memory, using the two-pointer method, we use a constant O(1) space for our solution.

There is another established algorithm named Rabin-Karp algorithm which uses hashing and two-pointer technique to solve this problem in O(n) time complexity. Feel free to try to implement that algorithm and tell us in the discussion about it.