AlgoDaily - Length of Longest Palindromic Subsequence

Good morning! Here's our prompt for today.

Question/Prompt

A palindrome is a word, phrase, or sequence that reads the same backward or forwards. A palindromic subsequence is a palindrome derived from a sequence by deleting some or no elements from it. This subsequence is formed without changing the order of the elements in the original sequence.

Given a string s, can you find the length of the longest palindromic subsequence of s?

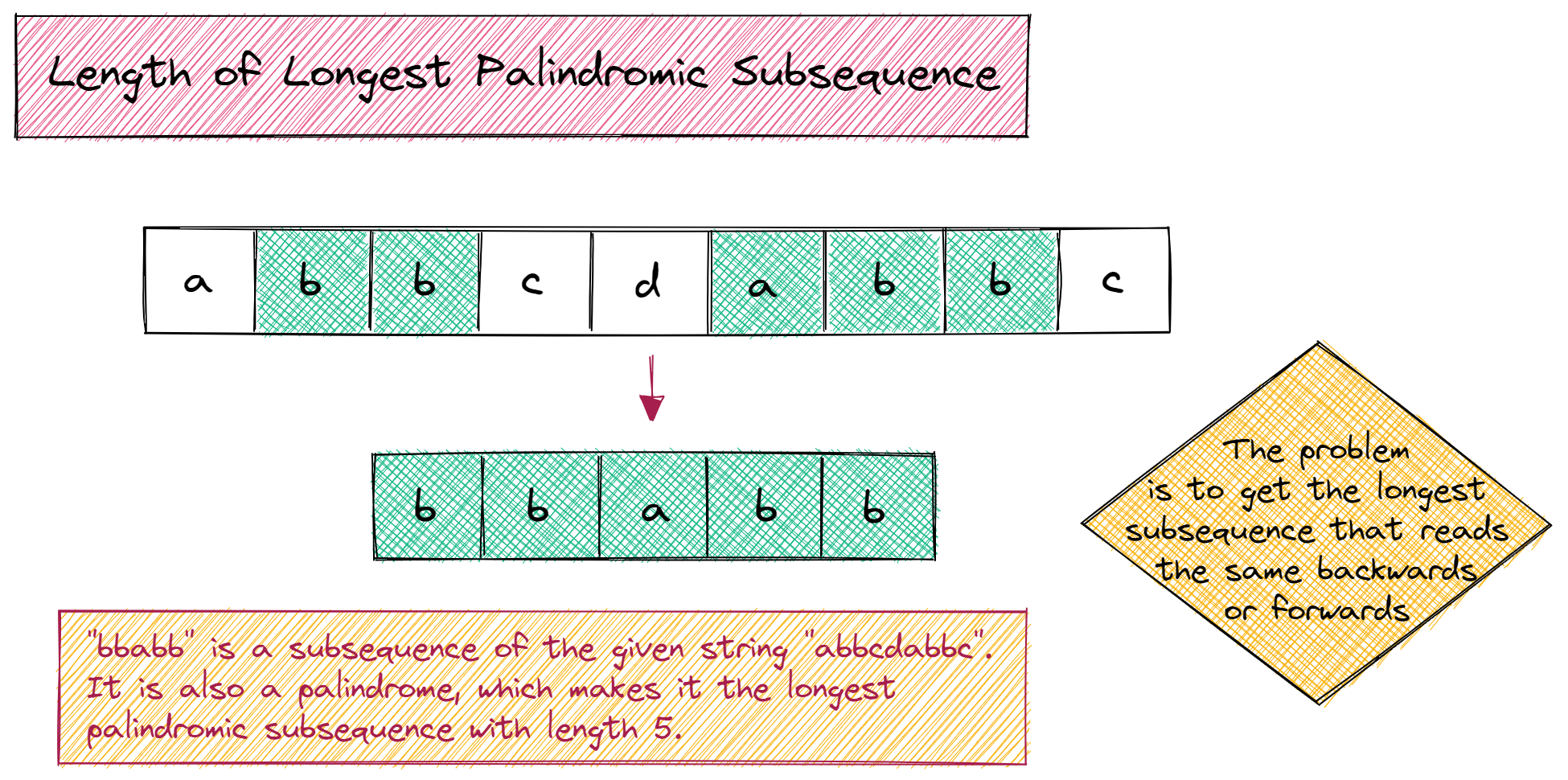
For example, if s = "bbbab", then the longest palindromic subsequence is bbbb. The length of this subsequence is 4, which is the required answer.

Constraints

1 <= s.length <= 1000
s consists only of lowercase English letters.

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
var assert = require('assert');
​
function longestPalindromeSubseq(s) {
    // add your code here
    return;
}
​
try {
    assert.deepEqual(longestPalindromeSubseq('bbbab'), 4);
    console.log('PASSED: ' + "`longestPalindromeSubseq('bbbab')` should return `4`");
} catch (err) {
    console.log(err);
}
​
try {
    assert.deepEqual(longestPalindromeSubseq('cbbd'), 2);
    console.log('PASSED: ' + "`longestPalindromeSubseq('cbbd')` should return `2`");
} catch (err) {
    console.log(err);
}
​
try {
    assert.deepEqual(longestPalindromeSubseq('abbcdabbc'), 5);
    console.log('PASSED: ' + "`longestPalindromeSubseq('abbcdabbc')` should return `5`");
} catch (err) {
    console.log(err);
}
​

Here's our guided, illustrated walk-through.

How do I use this guide?

Solution Walkthrough

By looking at the given string, the problem seems very simple. But programming a computer to solve it requires some thought. The first approach that may come to your mind is to directly check for palindromic subsequences and find the one with the longest length. Let's see how this would work.

Brute Force Approach

The brute-force approach is to find all possible subsequences of the given string and check if they are valid palindromes. From these palindromic subsequences, we want the subsequence with the longest length.

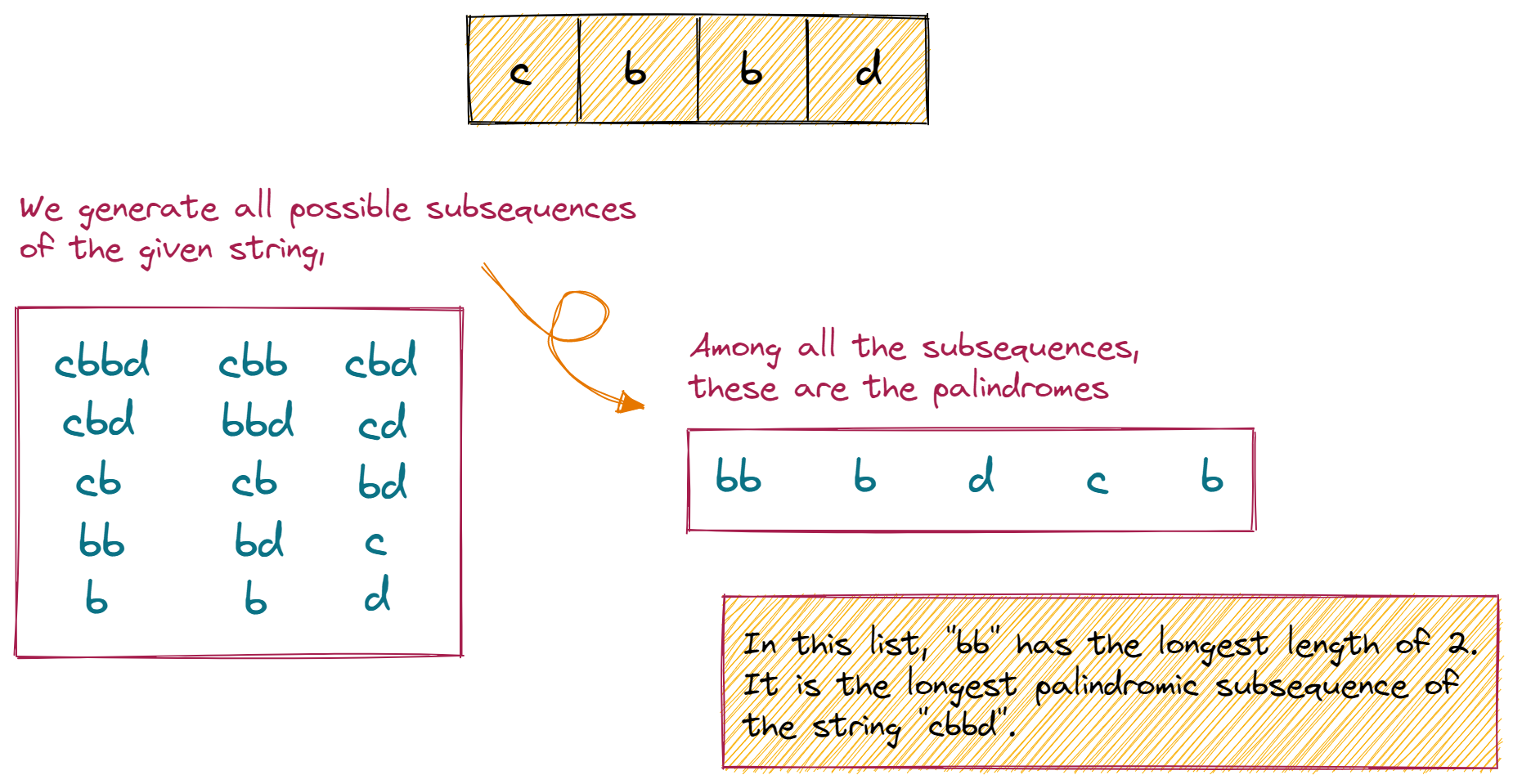
However, this approach is not an ideal one. Why? Because it can go up to exponential time complexity for longer strings. Can you think of a better, more efficient solution to this problem?

Dynamic Programming Approach

The time complexity issue for our problem can be reduced to an extent if we use the dynamic programming approach. It breaks down this complex, large problem into smaller subproblems that can be solved optimally.

For this problem, we will use the bottom-up dynamic programming approach (through tabulation). This approach requires us to initialize a 2D grid so that we can store the result of each subproblem and reference it later in constant time. This ensures that similar subproblems are not recomputed.

Build your intuition. Click the correct answer from the options.

Which of the following properties exist in this problem, that makes it solvable using dynamic programming approach?

Click the option that best answers the question.

Repeated Subproblems
Optimal Substructure
Sorted String
Both 1 and 2
Both 2 and 3

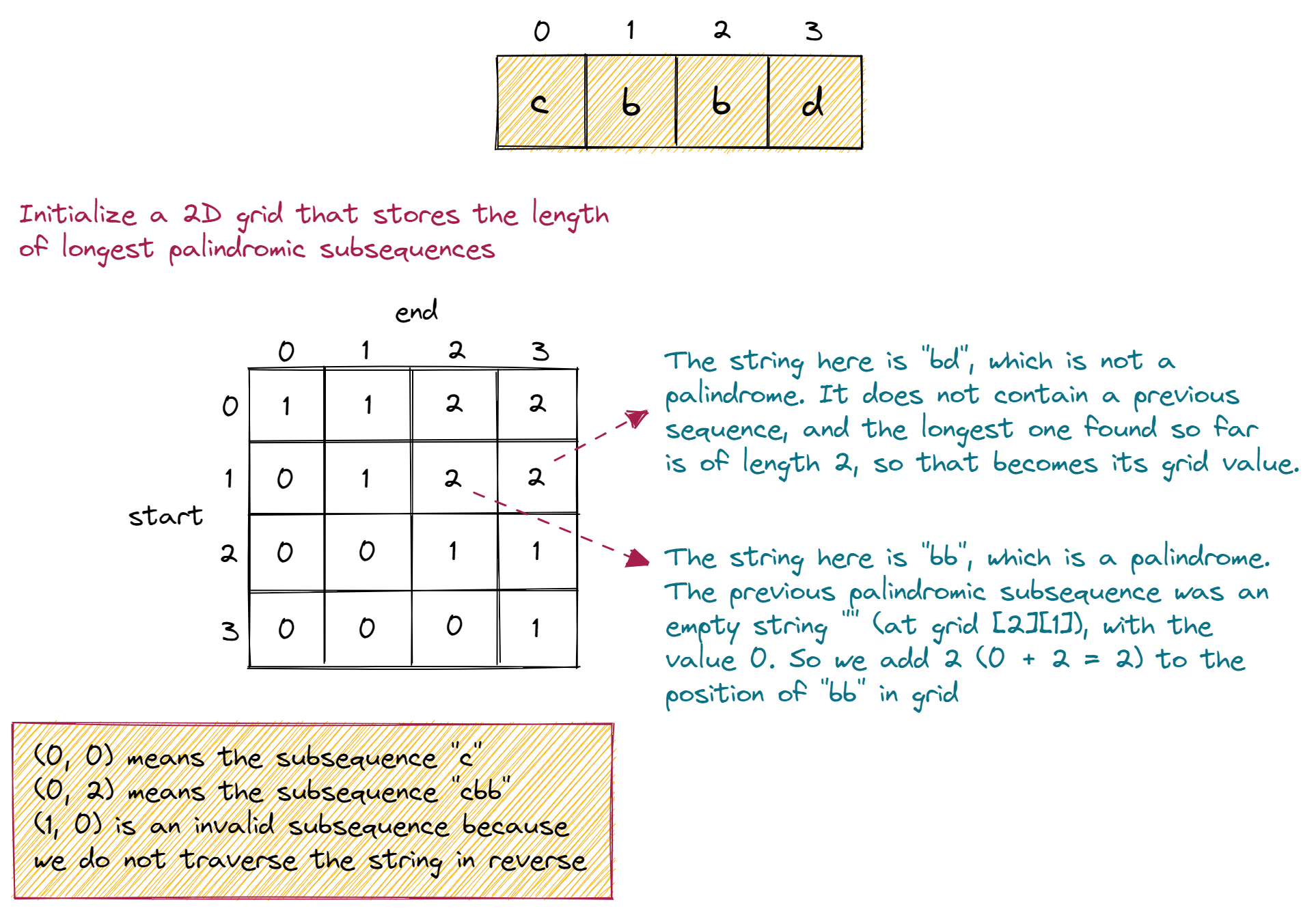
The rows and columns of the grid will be equal to the length of the given string s. Let's consider the given string s to be "cbbd". We will have a 4 x 4 grid in this case. Since we want to find the length of the longest palindromic subsequence, each cell in the grid will store the length of the longest palindromic subsequence encountered so far during the bottom-up traversal.

Now for the bottom-up traversal, two pointers are initialized at the start and end of the original string. Essentially, one pointer would traverse normally, while the other would work in reverse. This kind of traversal is required to check for palindromes (as they read the same forwards and backward) so that we only store the lengths of palindromic sequences in the grid.

SNIPPET

1for i in range(len(s) - 1, -1, -1): # works in reverse
2    for j in range(i + 1, len(s)): # traverses normally

Now start filling the table from the diagonal first, as the diagonals represent a single element (the start and end points will be the same, which means it is the same element). And if there is one character, then the length of the palindromic subsequence is 1. Hence, all the diagonals will be filled with the value 1.

SNIPPET

1grid[i][j] = 1

Try this exercise. Fill in the missing part by typing it in.

All the values below the diagonal are ___ because they are invalid subsequences.

Write the missing line below.

Now for elements that are not on the diagonal, check if the current subsequence contains any of the previously calculated palindromic subsequences. Based on this, there can be two cases,

If it contains a previous subsequence, then we add 2 to the length of the previous palindromic subsequence to get the length for the current sequence. We add 2 because a palindromic subsequence based on a previous one would always have 2 additional characters (the same character at the start and at the end).
If it does not contain a subsequence, then there is no new palindromic subsequence. The longest palindromic subsequence will remain as the longest one we have seen so far (no change), so the current cell would have the value of the length of the longest palindromic subsequence encountered so far.

Since we have approached the problem in a bottom-up manner, the last element that we would end up during our traversal is the top-right element of the grid. Returning its value should give us the value of the length of the longest palindromic subsequence.

Time Complexity

The time to create, traverse and fill the 2D grid of size n x n is n², which makes the time complexity of the solution as O(n²).

Build your intuition. Is this statement true or false?

This problem can also be solved using the memoization approach of dynamic programming.

Press true if you believe the statement is correct, or false otherwise.

One Pager Cheat Sheet

Find the length of the longest palindromic subsequence of a given string s, consisting of only lowercase English letters and with length no greater than 1000.
A brute-force approach to checking for the longest palindromic subsequence could be to directly check for palindromic subsequences and find the one with the longest length.
The brute force approach to finding the length of the longest palindromic subsequence involves checking all possible subsequences of the given string, and is not ideal due to its exponential time complexity.
We can reduce the time complexity of our problem by utilizing the bottom-up dynamic programming approach, which uses a 2D grid to store the result of each subproblem and reference it in constant time.
Dynamic programming is a technique used to solve problems through breaking them down into smaller subproblems that exhibit optimal substructure and overlapping subproblems, allowing us to solve them using a bottom-up tabulation approach to store the results of each subproblem.
We fill a 4 x 4 grid by traversing the given string s "cbbd" with two pointers, one working in reverse and the other traversing normally, to store the length of the longest palindromic subsequence encountered so far.
Fill the grid[i][j] with 1 for diagonals that represent one element, as the length of the palindromic subsequence for one character is 1.
All elements below the diagonal of the table should be set to 0 as they represent invalid subsequences due to their start point being after their end point.
We traverse the grid bottom-up to find the length of the Longest Palindromic Subsequence which is returned by the top-right element of the matrix.
The time complexity of the solution is O(n<sup>2</sup>), as it takes n² time to create, traverse and fill the 2D grid of size n x n.
The problem can be solved using the memoization approach of dynamic programming, reducing the time complexity to O(n<sup>2</sup>).

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function longestPalindromeSubseq(s) {
    if (!s) {
        return 0;
    }
    let grid = Array(s.length).fill('').map(() => Array(s.length).fill(0));
    for (let i = s.length - 1; i >= 0; i--) {
        grid[i][i] = 1;
        for (let j = i + 1; j < s.length; j++) {
            if (s[i] == s[j]) {
                grid[i][j] = grid[i + 1][j - 1] + 2;
            } else {
                grid[i][j] = Math.max(grid[i + 1][j], grid[i][j - 1]);
            }
        }
    }
    return grid[0][s.length - 1];
}
​
try {
    assert.deepEqual(longestPalindromeSubseq('bbbab'), 4);
    console.log('PASSED: ' + "`longestPalindromeSubseq('bbbab')` should return `4`");
} catch (err) {
    console.log(err);
}
​
try {
    assert.deepEqual(longestPalindromeSubseq('cbbd'), 2);
    console.log('PASSED: ' + "`longestPalindromeSubseq('cbbd')` should return `2`");
} catch (err) {
    console.log(err);

Alright, well done! Try another walk-through.

If you had any problems with this tutorial, check out the main forum thread here.