Now for elements that are not on the diagonal, check if the current subsequence contains any of the previously calculated palindromic subsequences. Based on this, there can be two cases,

• If it contains a previous subsequence, then we add 2 to the length of the previous palindromic subsequence to get the length for the current sequence. We add 2 because a palindromic subsequence based on a previous one would always have 2 additional characters (the same character at the start and at the end).
• If it does not contain a subsequence, then there is no new palindromic subsequence. The longest palindromic subsequence will remain as the longest one we have seen so far (no change), so the current cell would have the value of the length of the longest palindromic subsequence encountered so far.

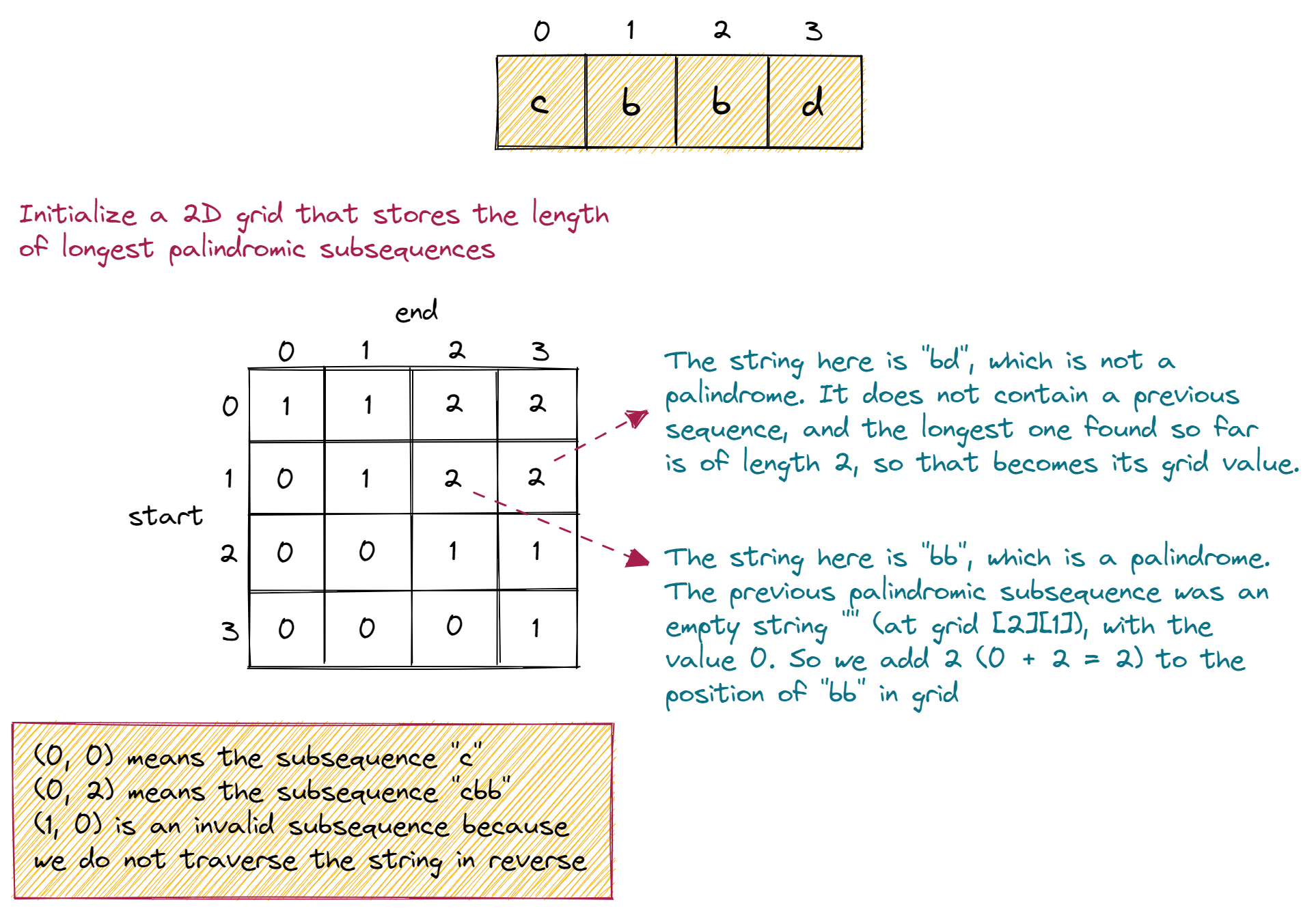
Since we have approached the problem in a bottom-up manner, the last element that we would end up during our traversal is the top-right element of the grid. Returning its value should give us the value of the length of the longest palindromic subsequence.