A lot of folks get tripped up by the majority part of this problem. The majority element is not the number with the most occurrences, but rather, it's the number value with >= 50% of "occurrences".

The brute force solution would be manually iterate through and count the appearances of each number in a nested for-loop, like such: given an array [4, 2, 4]:

1. iterate through for 4s, find 2 counts of 4
2. iterate through for 2s, find 1 count of 2
3. Realize that 2 > 3/2 (over half), so return 4

This is an O(n^2) solution because it would require passing through each number, and then at each number scanning for a count.

A better way to do this is to take advantage of the property of a majority element that it consists of more than half of the set's elements.

What do I mean by this? Let's take another example, [4, 2, 2, 3, 2].

2 is obviously the majority element in the example from a visual scan, but how can we tip the algorithm off to this? Well, suppose we sorted the array:

[2, 2, 2, 3, 4]

Notice that if we hone in on index 2, that we see another 2. This is expected-- if we sort an array of numbers, the majority element will represent at least 50% of the elements, so it will always end up at the Math.floor(nums.length / 2)th index.

Depending on the sorting algorithm, this technique is usually O(n * log n) and requires either O(1) space if the sort is in-place, or O(n) space if not.

Another Method

Yet another way to solve this is to use the speed of a hash map! Hash maps allow access/look-ups in constant time, and its keys are guaranteed to be unique.

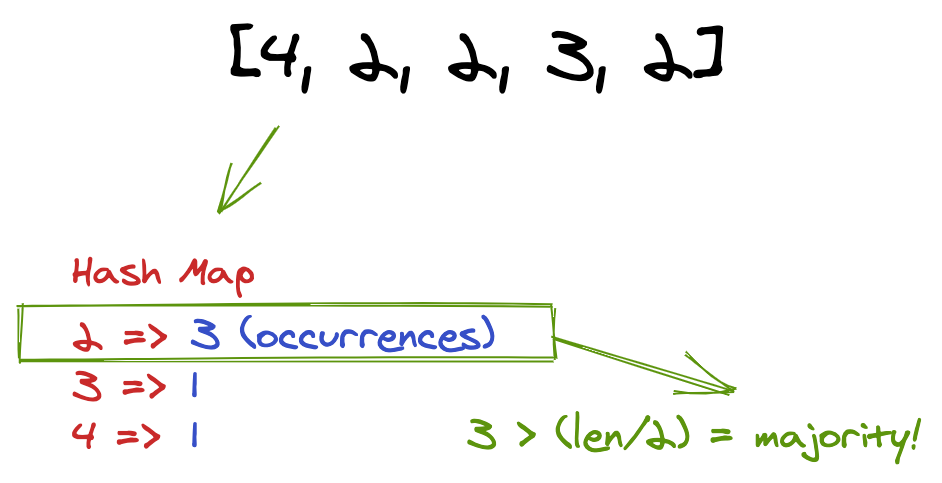
Thus, we can iterate through [2, 2, 2, 3, 4], and store each unique value as a key, and its attached value being the count. Each time we pass it, we increment its count, and use that information to relay we've got a current majority candidate.

1def majority_element(nums):
2  hash = {}
3  # we keep a local max variable to track what
4  # element is in the majority
5  max, val = 0, None
6
7  for i in range(0, len(nums)):
8    # increment or initialize the num as a key
9    if nums[i] in hash:
10      hash[nums[i]] += 1
11    else:
12      hash[nums[i]] = 1
13
14    if hash[nums[i]] > max:
15      max = hash[nums[i]]
16      val = nums[i]
17
18  return val
19
20print(majority_element([4, 2, 2, 3, 2]))

The time complexity of this solution is O(n) as it requires just one pass through the array, but has a space complexity of O(n) since it needs to maintain an auxiliary hash table.

One Pager Cheat Sheet

• The majority element of an array of length 100000, containing integer values between -1000000000 and 1000000000, can be found in O(n) time and O(n) space.
• The majority element is not the number with the most occurrences, but rather the one with more than 50% of the total "occurrences".
• By using a hash map to store unique values and their count, it is possible to find the majority element with an O(n) time complexity and O(n) space complexity.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx

    print("Nice job, 3/3 tests passed!")

###

# @param {number[]} nums

# @return {number}

###

from math import floor

​

​

def majority_element(nums):

    nums.sort()

    return nums[int(floor(len(nums) / 2))]

​

​

# print(majorityElement([1, 1, 1, 4, 2, 4, 4, 3, 1, 1, 1]))

​

​

import unittest

​

​

class Test(unittest.TestCase):

    def test_1(self):

        assert callable(majority_element) == True

        print("PASSED: 'majority_element' is a function")

​

    def test_2(self):

        assert majority_element([1, 4, 2, 4, 4, 3, 4]) == 4

        print("PASSED: 'majority_element([1, 4, 2, 4, 4, 3, 4])' should return '4'")

​

    def test_3(self):

        assert majority_element([1, 1, 1, 4, 2, 4, 4, 3, 1, 1, 1]) == 1

        print(

            "PASSED: 'majority_element([1, 1, 1, 4, 2, 4, 4, 3, 1, 1, 1])' should return '1'"

        )

That's all we've got! Let's move on to the next tutorial.

If you had any problems with this tutorial, check out the main forum thread here.