AlgoDaily - Split Set to Equal Subsets

Good morning! Here's our prompt for today.

We're given a set in the form of an array with a unique integers. Can you write a function that tells us whether it can be separated into two subsets whose elements have equal sums?

Here's an example: [5, 9, 7, 21]:

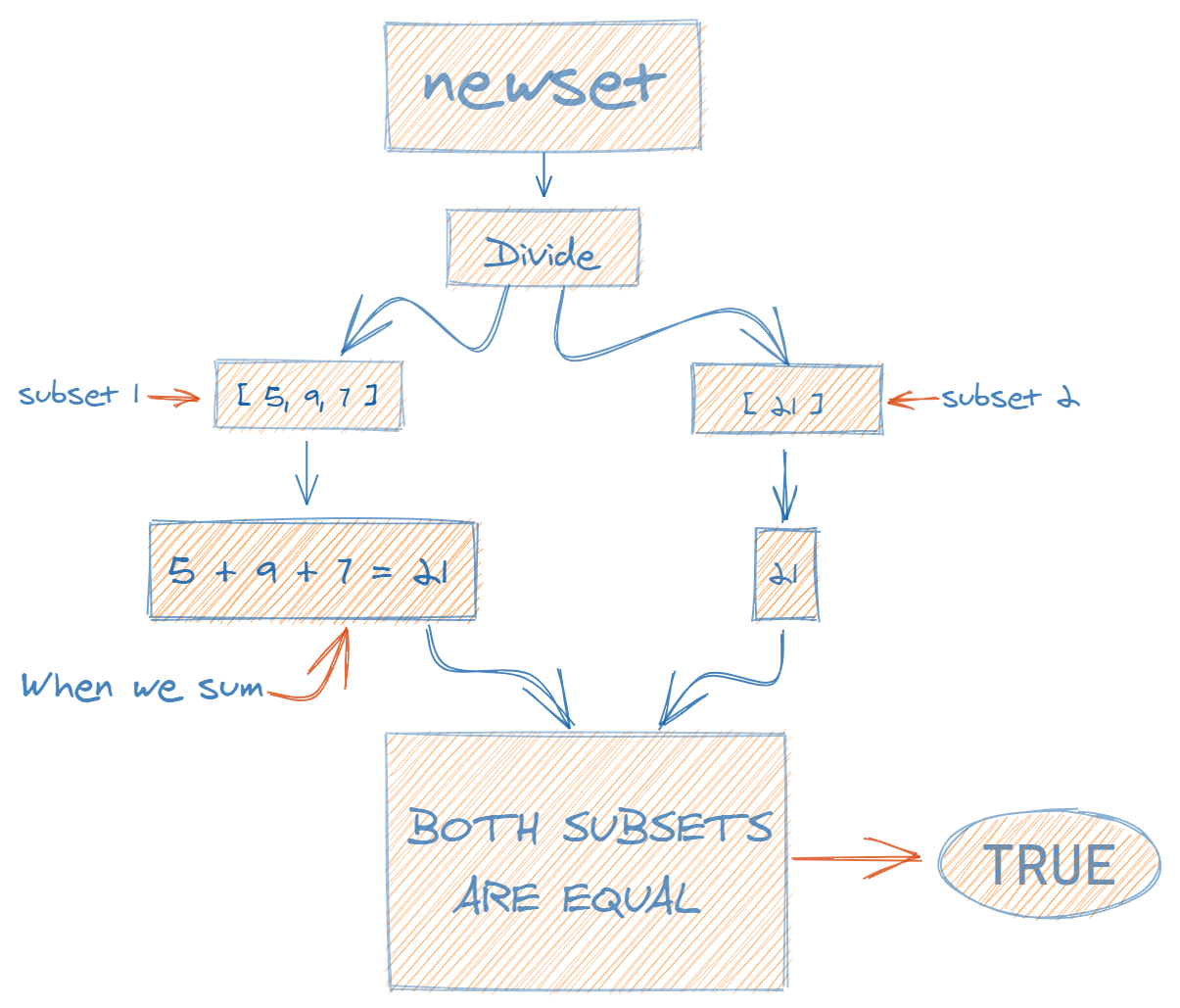
The below would return true because newSet can be divided into [5, 9, 7] and [21]. Both subsets sum to 21 and are equal.

JAVASCRIPT

1function hasEqualSubsets(arr) {
2  // fill
3}
4const newSet = [5, 7, 21, 9]
5
6console.log(hasEqualSubsets(newSet));   // true

And in another example, the below returns false since newSet cannot be divided into equal subsets.

JAVASCRIPT

1const newSet = [9, 3, 1]
2
3console.log(hasEqualSubsets(newSet));   // false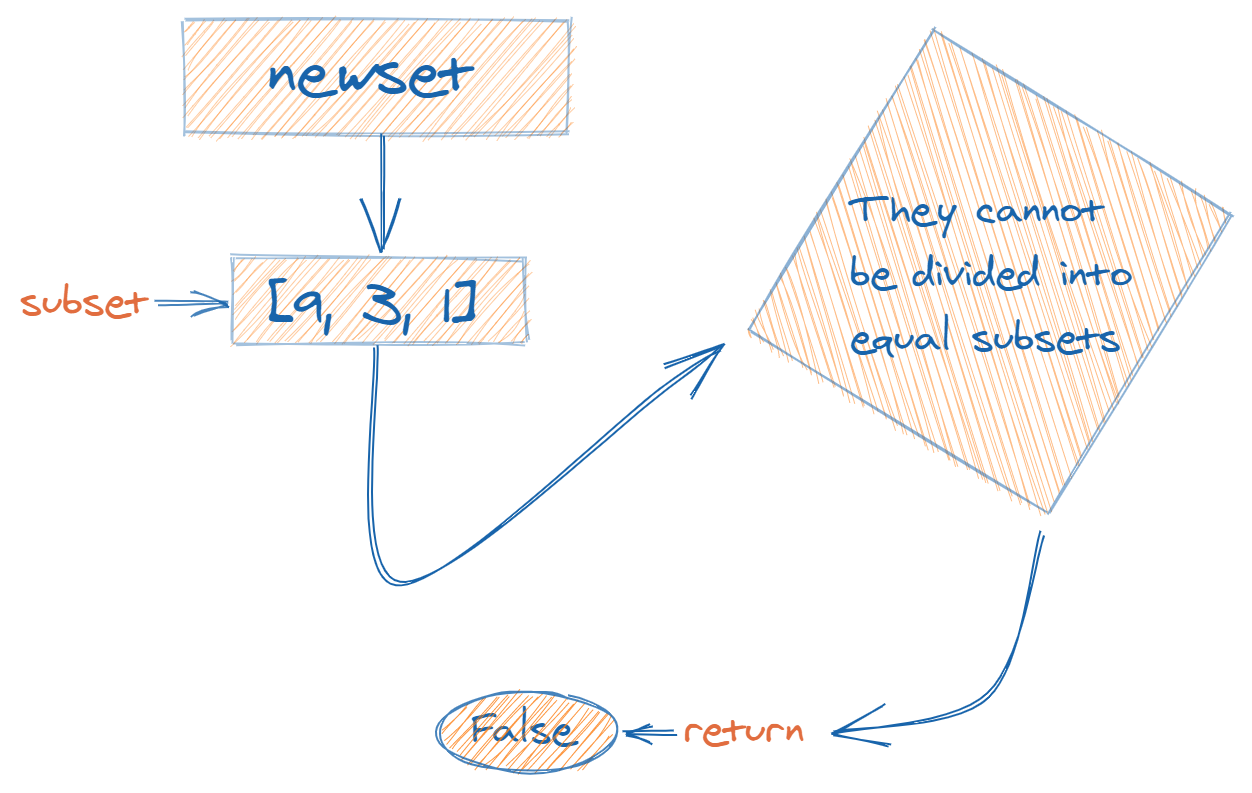

Constraints

Length of the array <= 1000
The values will always contain integer values between -1000 and 1000
The final answer will always fit in the integer value
Expected time complexity : O(n^2)
Expected space complexity : O(n^2)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
def has_equal_subsets(nums):
    return
​
​
import unittest
​
​
class Test(unittest.TestCase):
    def test_1(self):
        assert has_equal_subsets([14, 20, 9]) == False
        print("PASSED: has_equal_subsets([14,20,9]) should return False")
​
    def test_2(self):
        assert has_equal_subsets([3, 9, 5, 2, 9, 2, 8, 0, 11]) == False
        print("PASSED: hasEqualSubsets([3,9,5,2,9,2,8,0,11]) should return False")
​
    def test_3(self):
        assert has_equal_subsets([8, 13, 12, 20, 10, 0, 17, 3, 4]) == False
        print("PASSED: hasEqualSubsets([8,13,12,20,10,0,17,3,4]) should return False")
​
    def test_4(self):
        assert has_equal_subsets([5, 7, 21, 9]) == True
        print("PASSED: hasEqualSubsets([5, 7, 21, 9]) should return True")
​
    def test_5(self):
        assert (
            has_equal_subsets([18, 1, 5, 19, 5, 15, 15, 7, 19, 11, 8, 7, 13]) == False
        )
        print(

Here's how we would solve this problem...

How do I use this guide?

Access all course materials today

The rest of this tutorial's contents are only available for premium members. Please explore your options at the link below.

Returning members can login to stop seeing this.

Constraints

Try to solve this here or in Interactive Mode.

Here's how we would solve this problem...

Access all course materials today

Programming Categories

Popular Lessons